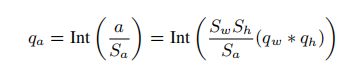《HAWQ-V3: Dyadic Neural Network Quantization》论文阅读

HAWQ-V3阅读笔记

Abstract

混合精度量化，integer-only，

Methodology

只采用均匀量化

权重对称量化，激活非对称量化，对量化步长S采用静态量化，采用per-channel的量化方式

3.1量化矩阵的乘法与卷积（核心：把浮点数的乘除改为二进制移位）

考虑一层隐藏激活为h，权值张量为W，然后是ReLU激活。首先，将h和W量化为Shqh和Swqw，其中Sh和Sw为实值量化尺度，qh和qW为对应的量化整数值。输出结果，用a表示，可以计算如下

a = SwSh(qw*qh)

其中qw*qh是用低精度的整数(如INT4)计算的矩阵乘法（或卷积），并以INT32精度累积。然后将此结果进行请求处理并发送到下一层，如下所示：

 

其中，Sa是输出激活的预先计算的比例因子

在HAWQ-V3中，qw⇤qh操作采用低精度的整数乘法和INT32累积，最终用SwSh/Sa对INT32结果进行量化。后者是一种浮点尺度，需要乘以累积的结果(以INT32精度)。一个幼稚的实现在这个阶段需要浮点乘法。但是，这可以通过强制将缩放设置为一个二进制数来避免。二进制数为b/2^c格式的有理数，其中b、c为两个整数。因此，方程中的一个二元缩放。4可以使用INT32整数乘法和位移位有效地执行。给定一个特定的SwSh/Sa，我们使用DN（表示二进制数）来表示可以计算相应的b和c的函数：

b/2^c = DN (SwSh/Sa).

除了避免浮点运算之外，还使用二进数的一个优点是，它消除了在硬件中支持除法（通常比乘法的延迟高一个数量级）的需要。该方法用于(Jacobetal.，2018)中的INT8量化，我们强制所有的调整为二进制的低精度和混合精度量化。

3.2BN

批一化(BN)是大多数神经网络体系结构的重要组成部分，特别是计算机视觉应用。BN对输入激活a执行以下操作：

 

其中µB和σB为a的均值和标准差，β，γ为可训练参数。在推理过程中，这些参数（包括统计参数和可训练参数）是固定的，因此BN操作可以与卷积相融合(见附录D)。然而，一个重要的问题是，量化BN参数往往会导致显著的精度下降。因此，许多先前的量化方法将BN参数保持在FP32精度中（例如（Cai等，2020；Chin等，2020；崔等，2018；董等，2020；Park等，2018b；张等，2018），仅2018）。这使得这种方法不适用于纯整数的硬件。虽然使用这种技术有助于提高准确性，但HAWQ-V3完全避免了这种情况。我们将BN参数与卷积融合，并用仅整数的方法将它们量化(请见图1，我们比较了BN和卷积的模拟量子化和HAWQ-V3)。

 

图1。卷积和批归一化折叠的假量化和真量化的说明。为简单起见，我们忽略了BN的仿射系数。（左）在模拟量化（又名假量化方法）中，权值和激活被模拟为具有浮点表示的整数，所有的乘法和积累都发生在FP32精度中。此外，使用FP32精度存储和计算BN参数（即µ和σ）。这是不可取的，但可以显著地帮助准确性，因为BN参数对量化很敏感。然而，使用这种方法，人们就不能从低精度的alu中获益。（右）卷积和BN折叠二元运算的整数管道的说明。BN中的标准差（σ）合并为权重的量化尺度，均值量化到INT32，作为偏差合并为权重（比32表示）注意，该方法将所有权值和激活都以整数格式存储，所有乘法都用INT4进行，以INT32精度累积。最后，将累积的结果通过二元缩放恢复到INT4中(用SσwSSah表示)。重要的是，不执行浮点运算，甚至不执行整数除法。详见第3.2节和附录D节。

这里要讨论的另一个重要问题是，我们发现(Jacobetal.，2018)中使用的氮折叠是次优的。在他们的方法中，BN层和CONV层融合在一起，而BN运行的统计数据仍在不断更新。这个操作需要计算每个卷积层两次，一次没有BN另一次有BN。然而，我们发现这是不必要的，并降低了准确性。相反，在HAWQ-V3中，我们遵循一种更简单的方法，首先保持Conv和BN层的展开，并允许BN统计数据进行更新。经过几个时代之后，我们冻结了BN层中的运行统计数据，并折叠了CONV和BN层(详见附录D)。正如我们将在第4节中展示的，与(Jacob等人，2018)相比，该方法具有更好的准确性。

3.3. Residual Connection

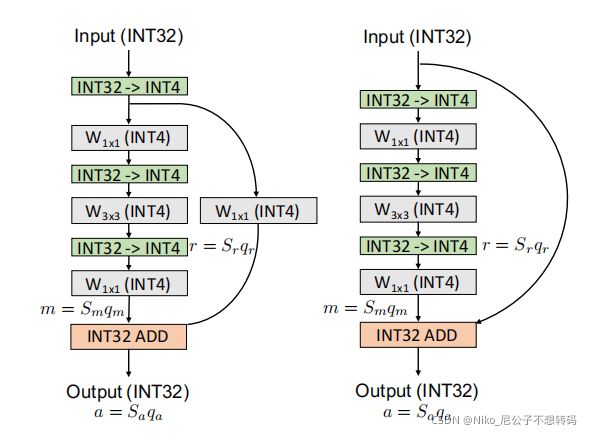
残余连接(Heetal.，2016)是许多神经网络架构中的另一个重要组成部分。与BN类似，残余连接的量化会导致精度下降，因此，一些前期量化工作以FP32精度执行操作（Choi等人，2018；Wang等人，2019；Zhang等人，2018）。人们有一个普遍的误解，认为这可能不是一个大问题。然而，这实际上导致了信号的完全丢失，特别是对于低精度的量化。这样做的主要原因是量化不是一个线性操作，即Q(a+b)6=Q(a)+Q(b)(a，b是浮点数)。因此，在FP32中执行累积并然后量化与累积量化值不相同。因此，不可能在仅使用智能设备的硬件中部署在FP32中保持剩余连接的量化方法(我们对此提供了更详细的讨论在附录F中，并量化由此产生的误差，可以超过90%)。我们在HAWQ-V3中避免了这一点，并使用INT32作为剩余分支。我们执行以下步骤，以确保加法运算可以进行二元运算。让我们将通过残差连接的激活表示为r=Srqr. 此外，让我们将残余添加前的主分支的激活情况表示为m=Smqm，以及通过=Saqa进行的残余积累后的最终输出情况。然后我们将有：qa=DN(Sm/Sa)qm+DN(Sr/Sa)qr。

注意，使用这种方法，我们只需要对qm执行二元缩放，并使用二缩放的qr添加结果。所有这些操作都可以只用纯整数算术进行。我们还应该注意到，在我们的方法中，所有的尺度都是静态已知的。图2将这些步骤进行示意图，用于有无降采样的剩余连接。对连接层也采用了类似的方法（见附录E）

 

3.4混合精度&ILP

假设我们有B个选择来量化每个层(即INT4或INT8的2)。对于具有L层的模型，ILP的搜索空间将为BL。解决ILP问题的目标是在这些BL可能性中找到最佳的位配置，从而在模型扰动⌦和用户指定的约束，如模型大小、BOPS和延迟之间进行最佳权衡。所有这些位精度设置可能会导致不同的模型扰动。为了使问题易于处理，我们假设每个层的扰动都是相互独立的

 

这些不用同时满足，由最终需求决定

我们在Python中使用开源PULP库(Roy&Mitchell，2020)来解决ILP，其中我们发现对于本文中测试的所有配置，给定灵敏度度量，ILP求解器可以在不到1秒内找到解决方案。相比之下，基于RL的方法(Wangetal.，2019)可能需要数十个小时才能找到正确的位精度设置。同时，我们可以看到，我们的ILP求解器可以很容易地用于多个约束。然而，由(Dongetal.，2020)提出的帕累托边界的复杂性在多个约束条件下呈指数级增长。在第4.2节中，我们展示了具有不同约束条件的结果。

3.5. Hardware Deployment

模型尺寸本身并不是衡量神经网络的效率（速度和能量消耗）的一个好指标。事实上，一个小的模型很有可能有更高的延迟，并消耗更多的能量来进行推断。FLOPs也是如此。原因是模型大小和流量p都不能解释缓存丢失、数据位置、内存带宽、硬件利用率不足等。为了解决这个问题，我们需要部署然后直接测量延迟。

我们针对T4GPU的英伟达图灵张量核心进行部署，因为它支持INT8和INT4的精度，并已增强用于深度学习网络推理。唯一可用的API是WMMA内核调用，它是一个用于在张量核心上以INT4精度执行矩阵-矩阵操作的微内核。然而，也没有现有的编译器可以使用WMMA指令将量化到INT4的NN映射到张量核心。为了解决这一挑战，我们工作的另一个贡献是扩展TVM(Chen等人，2018)，以支持与INT8具有/没有混合精度的INT4推理。这一点很重要，因此我们可以验证混合精度推理的速度好处。为了实现这一点，我们必须在图级IR和操作符调度中添加新的特性，以使INT4推理高效。例如，当我们执行内存规划、恒定折叠和操作符融合等优化时，在图级红外线中，涉及到4位数据。然而，在可字节寻址的机器上，单独操作4位数据会导致存储和通信的效率低下。相反，我们将8个4位元素打包到一个INT32数据类型中，并作为一个块执行内存移动。在最后的代码生成阶段，数据类型和所有内存访问都将针对INT32进行调整。通过采用类似于Cutlass的scheduling策略(NVIDIA，2020)，我们为TVM中的8位和4位数据实现了一种新的张量核心的直接卷积计划。我们为线程大小、块大小和循环顺序等配置设置了旋钮，以便TVM中的自动调谐器可以搜索最佳的延迟设置。

另一个重要的一点是，我们已经完成了pipeline来直接测试训练后的权值，并避免使用随机权值进行速度测量。这一点很重要，因为硬件实现之间的小差异可能不会被我们的神经网络训练框架(PyTorch)中的量化算法所注意到，后者不使用TVM进行前向和向后传播。为了避免这类问题，我们确保TVM和PyTorch之间的每一层和阶段的结果都与机器精度匹配，并且在硬件中使用仅整数运算执行时验证了最终的Top-1精度。在附录G中，我们给出了使用INT4量化的ResNet50特征图的误差积累，，它在PyTorch中使用伪量化，并部署在TVM中。

Results

在本节中，我们首先讨论了INT8、INT4和混合精度INT4/8有无蒸馏的各种模型(ResNetn18/50和Inceptionv3)上的ImageNet的结果。然后，我们研究了ILP公式的不同用例，以及模型大小、延迟和准确性之间的相应权衡。附录h提供了关于实施和设置的详细讨论。对于所有的实验，我们确保报告并与FP32中已知的基线NN模型的最高精度进行比较（即，我们使用一个强基线进行比较）。这一点很重要，因为使用较弱的基线精度可能会导致误导性的量化精度。

4.1. Low Precision Integer-Only Quantization Results

我们首先从RmageNet18/50和Inceptionv3的量化开始，并比较HAWQV3与其他方法的性能，如表1所示。

Uniform 8-bit Quantization

我们的8位量化实现了与基线相比相似的精度。重要的是，对于所有的模型，HAWQ-V3实现了比纯整数方法的更高的精度(Jacobetal.，2018)。例如，在ResNet50上，我们比(Jacob等al.，2018)高2.68%。这部分是由于我们在第3.2节中描述的BN折叠策略。

Uniform 4-bit Quantization

据我们所知，HAWQ-V3的4位结果是文献中报道的第一个仅限整数的量化结果。ResNet18/50和插入v3的精度结果相当高，尽管所有的推理计算都被限制为整数乘法、加法和位移。虽然有一些精度下降，但这不应该被错误地解释为统一的INT4是不有用的。相反，我们必须记住，某些用例有严格的延迟和内存占用限制，这可能是最好的解决方案。然而，通过混合精度的量化，可以获得更高的精度。

Mixed 4/8-bit Quantization

混合精度结果将所有模型的精度提高了几个百分点，同时略微增加了模型的内存占用。例如，ResNet18的混合精度结果比INT4版本高出1.88%，模型尺寸仅增加了1.9MB。蒸馏还可以进一步改进(在表中表示为HAWQV3+DIST)。对于ResNet50，蒸馏可以使混合精度提高1.34%。我们发现，蒸馏对混合精度量化的帮助最大，我们还发现对于统一INT8或统一INT4量化的情况几乎没有改善。

总的来说，结果表明，HAWQ-V3与之前的量化方法相当，包括均匀精度和混合精度量化(如PACT、RVQuant、One比特宽、HAQ、使用FP32算术和/或非标准比特精度，如5位，或权重和激活的不同位宽)。Inception-v3也适用于类似的观察结果，如表1c所示。

 

4.2. Mixed-precision Results with Different Constraints

在这里，我们将讨论可以对量化施加不同约束的各种场景，以及与每个场景相关的有趣的权衡。方程中的ILP问题。8有模型大小、bop和延迟的三个约束条件。我们考虑了每个约束条件的三个不同的阈值，并研究了ILP如何平衡这些权衡，以获得一个最优的量化模型。我们还关注了从业者对INT4量化的性能不满意，并希望通过混合精度量化(INT4和INT8)来提高性能（准确性、速度和模型尺寸）的情况。ILP公式使从业者能够设置每个或所有这些约束。在这里，我们给出了一次只设置其中一个约束时的结果。结果如表2所示，分别分为大小（模型大小）、BOPS和延迟三个部分。每个部分都表示由从业者指定的相应的约束。然后，ILP求解器找到最优的混合精度设置，以满足该约束，同时最大化精度。ResNet18的延迟约束示例见附录I。

我们从ResNet18的模型大小和BOPS约束开始。纯INT4量化的模型大小为5.6MB，INT8为11.2MB。然而，INT4量化的精度为68.45%，这对于特定的应用可能较低。然后，从业者可以选择将模型大小约束设置为略高于纯INT4。一种选择是选择7.9MB，它几乎在INT4和INT8之间。对于这种情况，ILP求解器会找到一个位精度设置，其精度为71.09%，几乎与INT8相同。该模型也比INT8的量化快6%。

另一种可能性是将速度/延迟设置为一个约束条件。此设置的结果在表2中的“延迟”行下表示。例如，从业者可以请求ILP找到一个位精度设置，这比INT8模型快19%的延迟（参见“介质”行）。这导致一个模型的精度为70.55%，模型大小仅为7.2MB。对BOPS也可以进行类似的约束。

从这些结果中，我们可以做出几个非常有趣的观察结果。(i)模型大小与BOPS之间的相关性较弱，这是预期的。这是一个更大的模型尺寸并不意味着更高的边界点，反之亦然。例如，比较ResNet18的中尺寸和高bop。后者的炸弹数量更低，尽管体积更大（实际上也更快）。(ii)模型尺寸与精度不存在直接关系。例如，对于ResNet50，High-BOPS的模型尺寸为22MB，精度为76.76%，而HighSize的模型尺寸较小，为21.3MB，但精度较高，为77.58%。

综上所述，虽然直接使用INT4量化可能会导致很大的精度下降，但与INT8的结果相比，我们可以以更快的推理速度显著提高精度。这给从业者提供了比INT8量化更广泛的选择。最后，我们应该提到的是，ResNet18/50和插入v3的所有结果的精度和速度已经通过TVM在硬件中执行量化精度时的直接测量来验证。因此，这些结果实际上是从业者将观察到的，而这些并不是模拟的结果。

 

Conclusions

在这项工作中，我们提出了HAWQ-V3，一个新的低精度仅整数量化框架，其中整个推理只执行整数乘法、加法和位移位。特别是，在整个推理中没有使用FP32算术甚至整数除法。我们给出了均匀和混合精度的INT4/8的结果。对于后者，我们提出了一种基于硬件感知的ILP的方法，该方法可以在模型扰动和应用程序特定约束之间，如模型大小、推理速度和总bop之间找到最优权衡。ILP问题可以非常有效地解决，对于这里考虑的所有模型。我们表明，与之前的(Jacobetal.，2018)的纯整数方法相比，我们的方法可以获得高达5%的准确率。最后，我们通过扩展TVM来支持INT4和INT4/8推断，直接在硬件上实现了低精度的量化模型。我们通过将每一层的激活与我们的PyTorch框架（达到机器精度）进行匹配，验证了所有的结果，包括验证模型的最终精度。该框架、TVM实现和量化模型都是开源的(HAWQ，2020)。