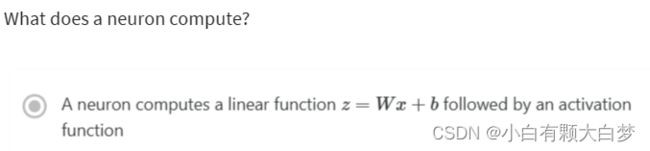吴恩达【神经网络和深度学习】Week2——神经网络基础
文章目录
- 1、Logistic Regression as a Neural Network
-
- 1.1、Binary Classification
-
- 1.1.1、Introduction
- 1.1.2、Notations
- 1.2、Logistic Regression
- 1.3、Logistic Regression Cost Function
- 1.4、Gradient Descent
- 1.5、Derivatives(导数)
- 1.6、More derivatives examples
- 1.7、Computation Graph
- 1.8、Derivatives with a Computation Graph
- 1.9、Logistic Regression Gradient Descent
- 1.10、Gradient Descent on m Examples
- 2、Python and Vectorization
-
- 2.1、Vectorization
- 2.2、More Vectorization Examples
- 2.3、Vectorizing Logistic Regression
- 2.4、Vectorizing Logistic Regression's Gradient Output
- 2.5、Broadcasting in Python
- 2.6、A Note on Python/Numpy Vectors
- 2.7、Quick tour of Jupyter/iPython Notebooks
- 2.8、Explanation of Logistic Regression Cost Function (Optional)
- 3、Quiz
- 4、Lab homework
-
- 4.1、Python Basics with Numpy
- 4.2、Logistic Regression with a Neural Network Mindset
1、Logistic Regression as a Neural Network
1.1、Binary Classification
1.1.1、Introduction
逻辑回归模型一般用来解决二分类(Binary Classification)问题。二分类就是输出y只有{0,1}两个离散值(也有{-1,1}的情况)。
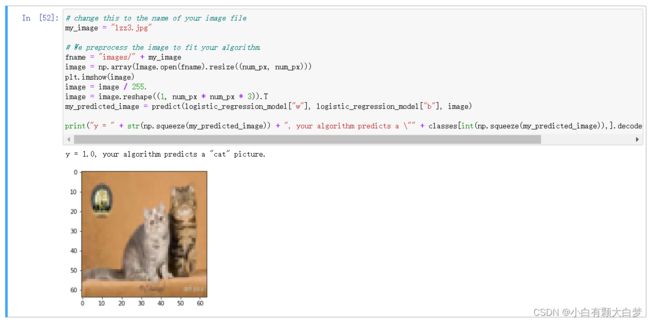
这里以一个图像识别问题为例,判断猫是否存在。

一般来说,彩色图片包含RGB三个通道。例如该cat图片的尺寸为(64,64,3)。在神经网络模型中,我们首先要将图片输入x(维度是(64,64,3))转化为一维的特征向量(feature vector)。方法是每个通道一行一行取,再连接起来。由于64x64x3=12288,则转化后的输入特征向量维度为(12288,1),每一个x案例都是一个(12288,1)的列向量。
实现代码:
def image2vector(image):
"""
Argument:
image -- a numpy array of shape (length, height, depth)
Returns:
v -- a vector of shape (length*height*depth, 1)
"""
v = image.reshape((image.shape[0] * image.shape[1]*image.shape[2], 1))
return v
1.1.2、Notations
- Sizes:
- m: number of examples in the dataset
- n x n_x nx: input size
- n y n_y ny: output size(or number of classes)
- n h [ l ] n_h^{[l]} nh[l]:number of hidden units of the l t h l^{th} lth layer
- Objects:
- x ( i ) ∈ R n x x^{(i)}\in R^{n_x} x(i)∈Rnx is the i t h i^{th} ithexample represented as a column vector.
- X ∈ R n x × m X \in R^{n_x\times m} X∈Rnx×m is the input matrix

- y ( i ) ∈ R n y y^{(i)}\in R^{n_y} y(i)∈Rny is output label the i t h i^{th} ithexample
- Y ∈ R n y × m Y \in R^{n_y\times m} Y∈Rny×m is the label matrix
For logistic regression:

1.2、Logistic Regression
Given x, we want y ^ = P ( y = 1 ∣ x ) \hat y=P(y=1|x) y^=P(y=1∣x) ( 0 ≤ y ^ ≤ 1 0\le \hat y \le 1 0≤y^≤1)
我们引入两个参数来辅助线性模型的建立:
- w ∈ R n x w \in R^{n_x} w∈Rnx
- b ∈ R b \in R b∈R
这样,逻辑回归的线性预测输出可以写成:
y ^ = w T x + b \hat y=w^Tx+b y^=wTx+b
但是这里的 y ^ \hat y y^仍是整个实数范围内的,我们要想把他映射到[0,1],还需要做一次sigmoid变换:
y ^ = s i g m o i d ( w T x + b ) \hat y=sigmoid(w^Tx+b) y^=sigmoid(wTx+b)
其中, s i g m o i d ( z ) = 1 1 + e − z sigmoid(z)=\frac{1}{1+e^{-z}} sigmoid(z)=1+e−z1
这样我们就可以把输出锁定在[0,1]之间
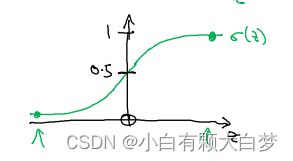
可以看出,当 z → ∞ z\rightarrow\infty z→∞时, s i g m o i d ( z ) = 1 1 + 0 = 1 sigmoid(z)=\frac{1}{1+0}=1 sigmoid(z)=1+01=1,便得出是猫的结论。
1.3、Logistic Regression Cost Function
最终的目标是 y ^ ≈ y \hat y\approx y y^≈y,所以我们的代价函数也要以此来展开,通过合理的 w , b w,b w,b值,来达到预期效果。
从单个样本出发,我们先定义损失函数:
一般来说,我们会想到: L o s s ( e r r o r ) f u n c t i o n : L ( y ^ , y ) = 1 2 ( y ^ − y ) 2 Loss(error)function: L(\hat y,y)=\frac{1}{2}(\hat y-y)^2 Loss(error)function:L(y^,y)=21(y^−y)2
但是,对于逻辑回归,我们一般不使用平方错误来作为Loss function。原因是这种Loss function一般是non-convex(非凸)的。non-convex函数在使用梯度下降算法时,容易得到局部最小值(local minumum),即局部最优化。而我们最优化的目标是计算得到全局最优化(Global optimization)。因此,我们一般选择的Loss function应该是convex的。
因而,我们可以构建另外一种Loss function,且是convex的:
L ( y ^ , y ) = − ( y l o g y ^ + ( 1 − y ) l o g ( 1 − y ^ ) ) L(\hat y,y)=-(ylog\hat y+(1-y)log(1-\hat y)) L(y^,y)=−(ylogy^+(1−y)log(1−y^))
我们来分析一下这个Loss function,它是衡量错误大小的,Loss function越小越好。
当y=1时, y ^ \hat y y^如果越接近1,表示预测效果越好;从此公式中我们可以看出, y = 1 y=1 y=1时 L ( y ^ , y ) = − ( l o g y ^ ) L(\hat y,y)=-(log\hat y) L(y^,y)=−(logy^),而 y ^ \hat y y^越接近1,loss function越小,如果 y ^ \hat y y^错误地接近0, − ( l o g y ^ ) -(log\hat y) −(logy^)会带来非常大的损失,这也就达到了我们的效果。y=0时同理。
拓展到m个样本:我们定义Cost function,Cost function是m个样本的Loss function的平均值,反映了m个样本的预测输出与真实样本输出y的平均接近程度。Cost function可表示为: J ( w , b ) = 1 m ∑ i = 1 m L ( y ^ ( i ) , y ( i ) ) J(w,b)=\frac{1}{m}\sum_{i=1}^{m}{L(\hat y^{(i)},y^{(i)})} J(w,b)=m1i=1∑mL(y^(i),y(i))
1.4、Gradient Descent
可以参考机器学习Week1里的第三部分,有一点区别是,参考链接里后面的应用时对于linear regression进行梯度下降,而本文是直接对于logistic regression进行分析,在1.9小节部分要注意甄别,两者主要是cost function的形式不同。
1.5、Derivatives(导数)
1.6、More derivatives examples
讲的是导数基础内容,比较简单就不再赘述了,如果不太了解的话可以参考导数-维基百科
1.7、Computation Graph
讲的是前向传播的过程,反向传播还没讲
正向传播是从输入到输出,由神经网络计算得到预测输出的过程;反向传播是从输出到输入,对参数w和b计算梯度的过程。
前向传播的Computation Graph可以用下面这样的图来表示:
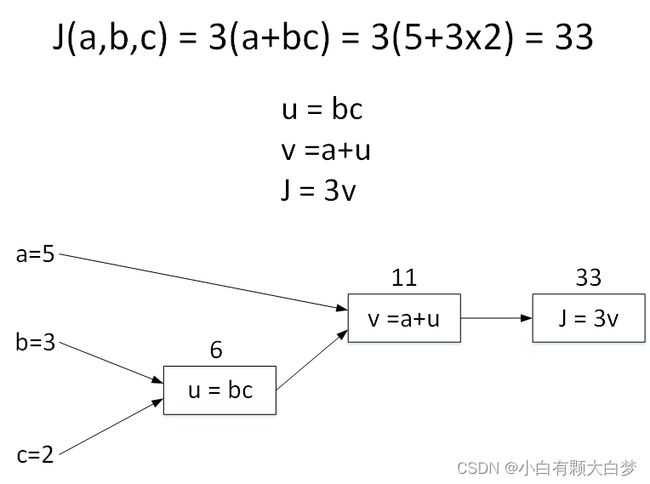
给定输入,得到输出的过程。
1.8、Derivatives with a Computation Graph
讲的是反向传播里面的计算导数,是通过中间过程的到计算输出对输入的偏导数。反映到线性回归上,是求出J对于w和b的偏导的最终过程。以上面的图为例:
∂ J ∂ b = ∂ J ∂ v ∂ v ∂ u ∂ u ∂ b = 3 ∗ 1 ∗ c = 6 \frac{ \partial J }{ \partial b }=\frac{ \partial J }{ \partial v }\frac{ \partial v }{ \partial u }\frac{ \partial u }{ \partial b }=3*1*c=6 ∂b∂J=∂v∂J∂u∂v∂b∂u=3∗1∗c=6
1.9、Logistic Regression Gradient Descent
对于单个样本,我们继续使用computation graph 来描述这一过程。
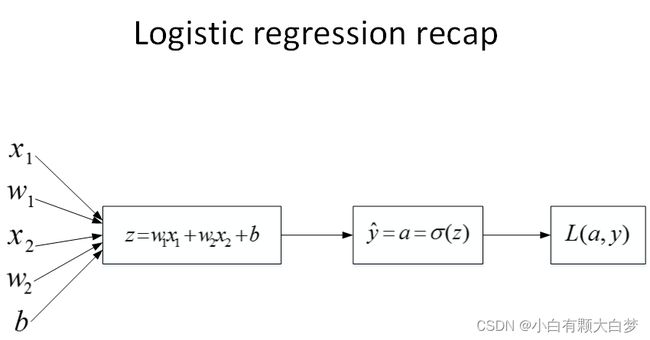
推导过程如下:
∂ L ∂ a = − y a + 1 − y 1 − a \frac{ \partial L }{ \partial a }=-\frac{y}{a}+\frac{1-y}{1-a} ∂a∂L=−ay+1−a1−y
∂ L ∂ z = ∂ L ∂ a ∂ a ∂ z = ( − y a + 1 − y 1 − a ) × a ( 1 − a ) = a − y \frac{ \partial L}{ \partial z }=\frac{ \partial L }{ \partial a }\frac{ \partial a }{ \partial z }=(-\frac{y}{a}+\frac{1-y}{1-a})\times a(1-a)=a-y ∂z∂L=∂a∂L∂z∂a=(−ay+1−a1−y)×a(1−a)=a−y
∂ L ∂ w 1 = ∂ L ∂ z ∂ z ∂ w 1 = x 1 × ( a − y ) \frac{ \partial L }{ \partial w_1 }=\frac{ \partial L }{ \partial z }\frac{ \partial z }{ \partial w_1 }=x_1\times(a-y) ∂w1∂L=∂z∂L∂w1∂z=x1×(a−y)
∂ L ∂ w 2 = ∂ L ∂ z ∂ z ∂ w 2 = x 2 × ( a − y ) \frac{ \partial L }{ \partial w_2 }=\frac{ \partial L }{ \partial z }\frac{ \partial z }{ \partial w_2 }=x_2\times(a-y) ∂w2∂L=∂z∂L∂w2∂z=x2×(a−y)
∂ L ∂ b = ∂ L ∂ z ∂ z ∂ b = ( a − y ) \frac{ \partial L }{ \partial b }=\frac{ \partial L }{ \partial z }\frac{ \partial z }{ \partial b }=(a-y) ∂b∂L=∂z∂L∂b∂z=(a−y)
之后逻辑回归的梯度下降就可表示为:
w 1 = w 1 − α ∂ L ∂ w 1 , w 2 = w 2 − α ∂ L ∂ w 2 , b = b − α ∂ L ∂ b w_1=w_1-\alpha \frac{ \partial L }{ \partial w_1 }, w_2=w_2-\alpha \frac{ \partial L }{ \partial w_2 },b=b-\alpha \frac{ \partial L }{ \partial b } w1=w1−α∂w1∂L,w2=w2−α∂w2∂L,b=b−α∂b∂L
1.10、Gradient Descent on m Examples
把这样的代价函数当做L: J ( w , b ) = 1 m ∑ i = 1 m L ( y ^ ( i ) , y ( i ) ) J(w,b)=\frac{1}{m}\sum_{i=1}^{m}{L(\hat y^{(i)},y^{(i)})} J(w,b)=m1∑i=1mL(y^(i),y(i))
然后意义求出其对各个参数的导数。

里面的 x 1 ( i ) x_1^{(i)} x1(i)是第 i i i个样本中的 x 1 x_1 x1
算法流程图如下所示
J=0; dw1=0; dw2=0; db=0;
for i = 1 to m
z(i) = wx(i)+b;
a(i) = sigmoid(z(i));
J += -[y(i)log(a(i))+(1-y(i))log(1-a(i));
dz(i) = a(i)-y(i);
dw1 += x1(i)dz(i);
dw2 += x2(i)dz(i);
db += dz(i);
J /= m;
dw1 /= m;
dw2 /= m;
db /= m;
里面涉及了很多for循环,会减慢速度,下一节将介绍更好的方法——矩阵的使用。
2、Python and Vectorization
在机器学习Week2里写了一部分python和向量化的基本语法,可以参考下。
2.1、Vectorization
深度学习算法中,使用向量化矩阵运算的效率要比使用for循环高得多。
z = w T x + b z = w^Tx+b z=wTx+b
# 被替代之前
for i in range(n_x)
z+= w[i] * x[i]
z += b
python的numpy库中的内建函数(built-in function)使用了SIMD指令。相比而言,GPU的SIMD要比CPU更强大一些。
2.2、More Vectorization Examples
Eg1:

当计算u时,非向量方法是一个for循环,向量方法是u=np.exp(v),同理还有np.log()\np.abs()等算法
Eg2:
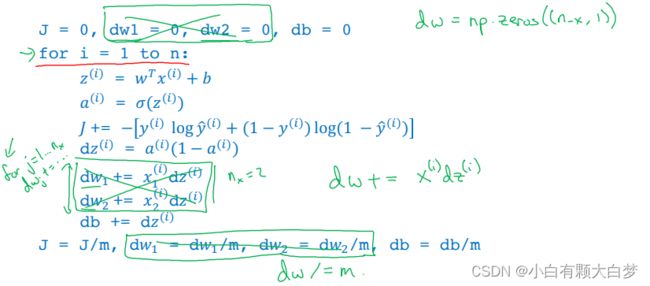
在1.10节提到的算法中进行改进, d w dw dw这里本是需要一个for循环的,现在把 d w dw dw改为一个向量,然后 d w + = x ( i ) d z ( i ) dw+=x^{(i)}dz{(i)} dw+=x(i)dz(i)
( d z ( i ) dz{(i)} dz(i)是个常数,所以可以让两个向量直接用)
d w = [ d w 1 , d w 2 … … , d w n x ] + = [ x 1 ( i ) d z ( 1 ) , x 2 ( i ) d z ( 2 ) … … x n x ( i ) d z ( n x ) ] dw=[dw_1,dw_2……,dw_{n_x}]+=[x_1^{(i)}dz^{(1)},x_2^{(i)}dz^{(2)}……x_{n_x}^{(i)}dz^{(n_x)}] dw=[dw1,dw2……,dwnx]+=[x1(i)dz(1),x2(i)dz(2)……xnx(i)dz(nx)]
2.3、Vectorizing Logistic Regression
z ( 1 ) = w T x ( 1 ) + b z^{(1)}=w^Tx^{(1)}+b z(1)=wTx(1)+b, z ( 2 ) = w T x ( 2 ) + b z^{(2)}=w^Tx^{(2)}+b z(2)=wTx(2)+b,…………
Now we can use Z = [ z ( 1 ) z^{(1)} z(1) z ( 2 ) z^{(2)} z(2) …… z ( m ) z^{(m)} z(m) ]= w T X + [ b … b … b ] w^TX+[b …b…b] wTX+[b…b…b],and A= [ a ( 1 ) a^{(1)} a(1) a ( 2 ) a^{(2)} a(2) …… a ( m ) a^{(m)} a(m)]= σ ( z ) \sigma(z) σ(z)
In python:
Z = np.dot(w.T,X)+b
A = sigmoid(Z)
2.4、Vectorizing Logistic Regression’s Gradient Output
不混淆的好方法就是先把分量形式写出来再总结成向量化形式
结合2.2节例2看,把所有待for循环的继续简化
- 对于 d z dz dz(2.2节例2好像是写错了,这个dz是用来算dw和db的中间量):
原来是对于每一个样本:for i =1 to n,都要计算一次dz值,现在直接把所有的dz存成一个向量

- 对于dw,最开始的时候我们要写 d w 1 + = dw_1+= dw1+=, d w 2 + = dw_2+= dw2+=……,然后在2.2节我们把dw弄成了向量的形式,直接 d w + = x ( i ) d z ( i ) dw+=x^{(i)}dz^{(i)} dw+=x(i)dz(i),现在我们要把+=给去掉

- 对于 d b db db, d b = 1 m × n p . s u m ( d z ) db = \frac{1}{m} \times np.sum(dz) db=m1×np.sum(dz)
2.5、Broadcasting in Python
英语翻译过来是广播,实际上就是教你处理矩阵和向量的时候把常数自动扩成列向量或者把列向量扩成矩阵。
例如:
[ 1 2 3 4 ] + 100 = [ 101 102 103 104 ] \left[ \begin{matrix} 1 \\ 2\\ 3 \\ 4 \\ \end{matrix} \right]+100=\left[ \begin{matrix} 101 \\ 102\\ 103 \\ 104 \\ \end{matrix} \right] 1234 +100= 101102103104
值得一提的是,在python程序中为了保证矩阵运算正确,可以使用reshape()函数来对矩阵设定所需的维度。这是一个很好且有用的习惯。
加和减都比较好理解,重点是乘和除:数组的乘除与矩阵不同,只有对应位置上单个数的运算,与 np.dot()区分开 ,后者是矩阵乘法。
a = np.array([1.0, 2.0, 3.0])
b = a
print(a*b)
# [1. 4. 9.]
机制
- 输出数组的shape是输入数组shape的各个轴上的最大值
- 如果输入数组的某个轴和输出数组的对应轴的长度相同或者其长度为1时,这个数组能够用来计算,否则出错
- 当输入数组的某个轴的长度为1时,沿着此轴运算时都用此轴上的第一组值
详细一点可以参考Broadcasting
2.6、A Note on Python/Numpy Vectors
一些小技巧来减少bug

最上面的那种情况既不是列向量也不是行向量,叫做rank 1 array,并不建议使用,推荐使用下面两种。
同时可以用
assert(a.shape == (5,1))
来判断向量维度,如果不是这个就会显示AssertionError
如果我们使用了rank 1 array,可以用reshape来改正
a.reshape(5,1)
2.7、Quick tour of Jupyter/iPython Notebooks
介绍了一下怎么使用朱皮特,略
2.8、Explanation of Logistic Regression Cost Function (Optional)
If y = 1 y=1 y=1: p ( y ∣ x ) = y ^ p(y|x)=\hat y p(y∣x)=y^,If y = 0 y=0 y=0: p ( y ∣ x ) = 1 − y ^ p(y|x)=1-\hat y p(y∣x)=1−y^
p ( y ∣ x ) p(y|x) p(y∣x)可以理解成预测成功的概率
将两者合并就可以写成: p ( y ∣ x ) = y ^ y ( 1 − y ^ ) ( 1 − y ) p(y|x)=\hat y^y(1-\hat y)^{(1-y)} p(y∣x)=y^y(1−y^)(1−y)
由于log函数的单调性,取log之后不影响结果属性:
l o g P ( y ∣ x ) = ( y l o g y ^ + ( 1 − y ) l o g ( 1 − y ^ ) ) logP(y|x) =(ylog\hat y+(1-y)log(1-\hat y)) logP(y∣x)=(ylogy^+(1−y)log(1−y^))
我们希望上述概率P(y|x)越大越好,对上式加上负号,则转化成了单个样本的Loss function,越小越好,也就得到了我们之前介绍的逻辑回归的Loss function形式:
L ( y ^ , y ) = − ( y l o g y ^ + ( 1 − y ) l o g ( 1 − y ^ ) ) L(\hat y,y)=-(ylog\hat y+(1-y)log(1-\hat y)) L(y^,y)=−(ylogy^+(1−y)log(1−y^))
对于m个样本而言:

损失函数跟对数形式的似然函数很像,只是在前面乘以 1 m \frac{1}{m} m1。最大似然估计的方法要求 l o g L ( p ) logL(p) logL(p)的最大值,损失函数在其前面加上负号,就是求最小值,这个跟损失函数的特性刚好吻合。1/m是用来对m个样本值的损失函数值取平均,不会影响函数功能。
因此,逻辑回归的损失函数求最小值,就是根据最大似然估计的方法来的。
更细致的理解可以看Logistic Regression(逻辑回归)中的损失函数理解
3、Quiz
Correct, we generally say that the output of a neuron is a = g(Wx + b) where g is the activation function (sigmoid, tanh, ReLU, …).
- Consider the following code snippet:
a.shape = (3, 4)
b.shape = (4, 1)
for i in range(3):
for j in range(4):
c[i][j] = a[i][j]*b[j]
How do you vectorize this?
:c=a*b.T
4、Lab homework
4.1、Python Basics with Numpy
- For example, if
x = [ 0 3 4 2 6 4 ] x = \begin{bmatrix} 0 & 3 & 4 \\ 2 & 6 & 4 \\ \end{bmatrix} x=[023644]
then
∥ x ∥ = np.linalg.norm(x, axis=1, keepdims=True) = [ 5 56 ] \| x\| = \text{np.linalg.norm(x, axis=1, keepdims=True)} = \begin{bmatrix} 5 \\ \sqrt{56} \\ \end{bmatrix} ∥x∥=np.linalg.norm(x, axis=1, keepdims=True)=[556]
详细一点的各种范数:numpy.linalg.norm - 用于将图片转换成样本
def image2vector(image):
"""
Argument:
image -- a numpy array of shape (length, height, depth)
Returns:
v -- a vector of shape (length*height*depth, 1)
"""
v = image.reshape((image.shape[0] * image.shape[1]*image.shape[2], 1))
return v