(1.5.2.0)编程之美思路总结
- 数学类
- 零编程之美 set 0 求二进制数中1的个数
- 一编程之美 set 1 不要被阶乘吓倒
- 二编程之美 set 2 精确表达浮点数
- 三编程之美 set 3 最大公约数问题
- 四编程之美 set 4 找到符合条件的数
- 五编程之美 set 5 寻找数组中最大值和最小值
- 六编程之美 set 6 寻找最近点对
- 七编程之美 set 7 求数组中的最长递增子序列
- 八编程之美 set 8 区间重合判断
- 九编程之美 set 9 字符串移位包含问题
- 十编程之美 set 10 队列中取最大值操作问题
- 十一编程之美 set 11 买书问题
- 十二编程之美 set 12 快速找出故障机器
- 十三编程之美 set 13 光影切割问题
- 十四编程之美 set 14 小飞的电梯调度算法
- 十五编程之美 set 15 拈游戏分析1
- 十六编程之美 set 16 24点游戏
- 游戏类
//target:
//author;
//time;
//cin:
//test:nor:正常输入
// bor:边界
// exc:异常数学类
零、编程之美 set 0 求二进制数中1的个数
解法1:除以一个2,原来的数字将会减少一个0。如果除的过程中有余,那么就表示当前位置有一个1。 不断除2找余==1的个数
解法2:不断移位+与00000001进行”与”操作。如果结果为1,则表示当前八位数的最后一位为1,否则为0。
解法3:X=X&(X-1)到X为0的循环次数
- (1.5.2.1)求二进制数中1的个数
一、编程之美 set 1 不要被阶乘吓倒
题目
1. 给定一个整数 N, 那么 N 的阶乘 N! 末尾有多少个 0 呢
2. 求解 N! 的二进制表示中最低位 1 的位置
思路
1. 第一道题相当于求解 N! 分别是 2^a 和 5 ^b, 第二道题是 2^a
2. 公式: Z = [N/5] + [N/5^2] +… [N/5] 表示不大于 N 的数中 5 的倍数贡献一个 5, [N/5^2]表示不大于 N 的数中, 5^2 再贡献一个5
2. 但第一题有一个可以优化的地方, 因为 b < a, 所以只要关注 5^b 即可
代码
int ret = 0;
while(N) {
ret += N/5;
N /= 5;
}
int ret = 0;
while(N) {
N >>= 1;
ret += N;
}
- (1.5.2.2)不要被阶乘吓倒
二、编程之美 set 2 精确表达浮点数
有限小数和无限循环小数转化成分数
比如 0.9 -> 9/10 –>0.9*10^1/10^1
0.333(3) -> 1/3
解法
1. 主要涉及到一个数学公式的计算.
2. 对于有限小数, 转为整数,分子分母求最大公约数即可
3. 对于无限循环小数, 第一步是将非循环部分剔除. 仅讨论循环部分.
4.X=(a1a2…an+Y)/10^n
=(a1a2…an+b1b2…bm/(10^m-1))/10^n
=((a1a2…an)*(10^m-1)+(b1b2…bm))/((10^m-1)*10^n)
- (1.5.2.6)精准表达浮点数
三、编程之美 set 3 最大公约数问题
解法
1. f(x,y) = f(y, y%x) (y>0) 辗转相除法
2. 取模运算较为耗时, 将取模变成相减. 但对极端数据效果很差, 比如 gcd(1000,1)
3. 分析公约数的特点.
3.1 若 x,y 均为偶数, 那么 f(x,y) = 2*f(x/2, y/2)
3.2 若 x 为偶数, y 为奇数, 那么 f(x,y) = 2*f(x/2, y)
3.3 若都为奇数, f(x,y) = f(x, x-y) 那么下一步肯定有一个偶数
3.4 这样一来, 时间复杂度下降到 o(log(max(x,y)))
- (1.5.2.7)最大公约数
四、编程之美 set 4 找到符合条件的数

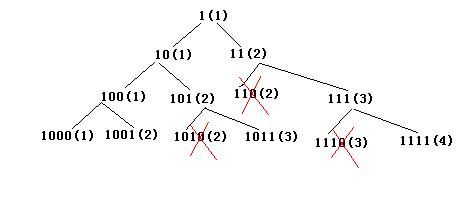
题目
任意给定一个正整数 N, 求一个最小的正整数 M (M > 1), 使得 N*M 的十进制表达式中只有 0 和 1.
解法
1. 枚举0,1能够组成的数字, 可以组成一颗二叉树
然后由 BFS 算法最终能够得到目标解. 但时间复杂度太高
2. 优化. 考虑对每一个节点加上一个属性, 对 N 求余的值. 假设两个节点X, Y的余相同, 那么由该节点扩展的下一层的 4 个子节点, 分别为 10*X, 10*X+1, 10*Y, 10*Y+1. 由取模的定理知道 10*X MOD N == 10*Y MOD N, 10*X +1 MOD N == 10*Y +1 MOD N
假设 X < Y, 那么 Y 节点的存在便失去了意义. 因为假如 X,Y 对 N 取模为0, 那么返回的结果肯定在 X 的子树上
时间复杂度的计算. 因为对N求余有 N 个节点, 所以每一层的搜索空间由 指数大小缩小到 o(n) 大小
- (1.5.2.8)找出相乘结果只有0和1的整数
五、编程之美 set 5 寻找数组中最大值和最小值
3、
解法
1. 设置 min, max 两个变量, 然后遍历一遍数组, 比较次数为 2*N
2. 依然设置 min, max 两个变量并遍历数组, 但将遍历的 step 设置为 2, 比较次数为 1.5 * N
3. 改变数组的做法. 先排个序
使得 min 总是在偶数位置, max 总在奇数位置, 比较次数依然是 1.5*N
4. 分值算法, 实际上就是归并算法的变形
实现较为复杂, 但事件复杂度依然为 1.5N
- (1.5.2.9)寻找数组的最大值和最小值
六、编程之美 set 6 寻找最近点对
算法
核心是分治算法
1. 分别根据点的 x,y 值进行排序
2. 在 x 轴上划一道垂线, 将点均分成两半
3. 假设最近点对都在左/右部分, 递归计算左/右半部分的最短距离并返回较小值 dis
4. 假设最近点对分别在左右两个部分, 横跨中心的竖线. 中心线为中心, 2*dis 为宽度画一个矩形, 横跨中心线的最近点对 candidate 都在这个矩形内. 将这些点按照 y 值的大小加入到数组中. 遍历数组中的点, 将该点与其后的 7 个点计算距离, 返回最小距离
5. 为什么仅和 7 个点作对比呢. 因为已经假设 dis 是左右不分最近点对的最小值, 这就说明在一个长(宽)为 dis 的正方形内, 至多有 4 个点. 长为 dis*2, 宽为 dis 的长方形至多 8 个.
- (1.5.2.10)寻找最近点对
七、编程之美 set 7 求数组中的最长递增子序列
解法
法一:
以序列1,-1,2,-3,4,-5,6,-7
使用i来表示当前遍历的位置
当i=1时,显然,最长的递增序列为(1),序列长度为1.
当i=2是,由于-1<1。因此,必须丢弃第一个值后重新建立串。当前的递增序列为(-1),长度为1。
当i=3时,由于2>1,2>-1。因此,最长的递增序列为(1,2),(-1,2),长度为2。在这里,2前面是1还是-1对求出后面的递增序列没有直接影响。(但是在其它情况下可能有影响)
依此类推之后,我们得出如下的结论。
假设在目标数组array[]的前i个元素中,最长递增子序列的长度为LIS[i]。那么,
LIS[i+1]=max{1,LIS[k]+1},array[i+1]>array[k],for any k <= i
即如果array[i+1]大于array[k],那么第i+1个元素可以接在LIS[k]长的子序列后面构成一个更长的子序列。于此同时array[i+1]本身至少可以构成一个长度为1的子序列。
按照这个动规的思路, 每次求 LIS[i] 是都要遍历 LIS[0] ~ LIS[i]
时间复杂度为 o(n^2)
法二: (1) 是一个比较一般性的解法. 考虑下面一个例子
目标序列为 1, -1, 2, -3, 4, -5, 6, 当 i = 4 时, 最长的递增序列是 (1,2), (-1,2) 那么 4 > 2, 就可以直接把 4 加到前面的子序列中形成一个新的递增子序列
受此启发, 我们希望找到前 i 个元素中的一个递增子序列, 使得这个递增子序列的最大元素比 array[i+1] 要小, 且长度尽可能的长. 这样将 array[i+1] 加在该递增子序列后, 便可找到以 array[i+1] 为最大元素的最长递增子序列
长度为 1 的递增子序列最大元素的最小值为 MAXV[1] (最大元素是指长度为 i 的序列中最后一个元素, 最小值是指满足长度为 i 的所有序列中第 i 个值最小的那个)
。。。
长度为 LIS[i] 的递增子序列最大元素的最小值为 MAXV[LIS[i]]
假如有了这些值, 那么可以倒序的查找, 更新
MAXV[] 是一个递增数组, 可以使用二分查找法, 因此时间复杂度降低到 NlogN
法三:先对数组排序,然后找出原数组和排序后数组的LCS,就是我们要找的最长递增子序列。
1 ,-1,2,-3,4,-5,6,-7
-7,-5,-3,-1, 1 , 2 , 4 , 6
八、编程之美 set 8 区间重合判断
Leetcode 上有连续的两道题, 一个是 insert interval, 一个是 merge interval, 其中 insert interval 是 merge interval. 其中 insert interval 还是 merge interval 的扩展, 即便看起来相反
解法
1. 先对目标区间进行处理, 先排序后 merge, 时间复杂度为 o(nlogn)
2. 使用二分查找, 找到一个区间, 然后看该区间是否包含源区间
3. 因为目标区间是非连续的, 所以(2) 只要找出一个区间就好
九、编程之美 set 9 字符串移位包含问题
题目
给定字符串 s1 和 s2, 要求判定 s2能否能够被通过 s1 做循环移位得到的字符包含. s1 = AABCD, s2 = CDAA 返回 true. 给定 s1 = ABCD 和 s2 = ACBD 返回 false
解法
1. 最直接的方法是对 s1 进行移位然后比较. 若 s1 较长, 那么效率较低
2. 题目转化成比较 s2 是否在 s1s1 中, 这样可以利用 kmp 等算法提高对比效率
十、编程之美 set 10 队列中取最大值操作问题
题目
假设有这样一个拥有三个操作的队列
1. Enqueue(v)
2. Dequeue()
3. MaxEle()
请设计一种数据结构和算法, 让 MAXELE 操作的时间复杂度尽可能的低
法一:构建大顶堆
队列本身要么顺序结构要么链接结构,还那么存。另外对于队列每个元素构建一个节点(包含在队列中的位置),这些节点构成一个最大堆,因此插入和删除操作都要维护这个最大堆,时间复杂度都是O(LogN),取最大值的复杂度为 O(1)。
法二:双栈-pop-push-min
一个链表保存数值,另一个链表保存第一个链表中,对应节点范围内的最小值所在节点
假如队列的一次输入 1 3 2 4 2
那么对应堆栈的输入 1 3 2 4 2
0 1 -1 3 -1
当队列需要输出时, stackA 的数据转到 stackB 中, 数据变成 2 4 2 3 1 (0 1 -1 -1 -1)
注意, 最后输出的时候, 要比较 stackA.max() 和 stackB.max()
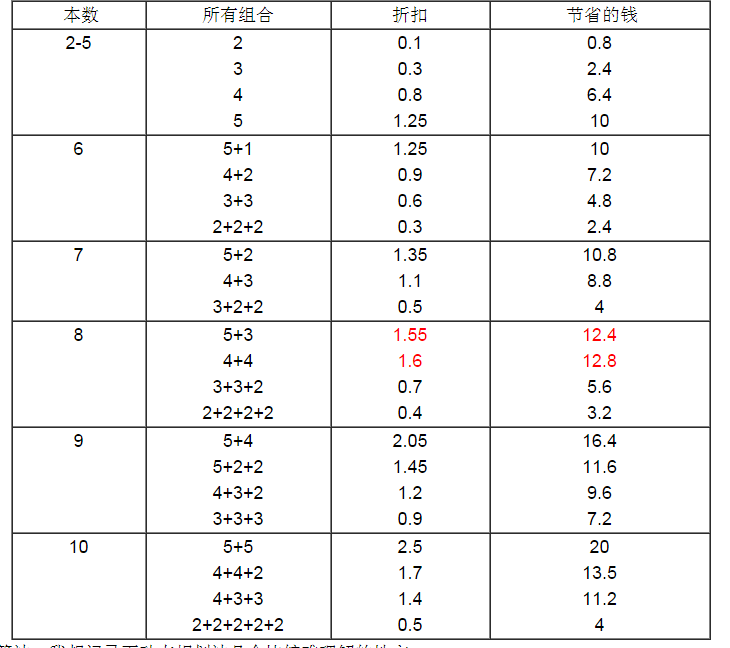
十一、编程之美 set 11 买书问题
问题描述
《哈利波特》系列一共有五卷,每一卷售价均8欧元。同时买不同的卷(各一本)有折扣,具体如下表所示。
2本优惠 5%, 3本 10%, 4 本 20% 5 本 25%
设计算法, 求解购买一本书的最低价格
法二:动态规划
假设输入为:1本卷1,2本卷2,2本卷3,2本卷4,1本卷5
购买组合及其折扣
5*0.25+3*0.1=1.55
4*0.2+4*0.2=1.6
3*0.1+3*0.1+2*0.05=0.7
2*0.05+2*0.05+2*0.05+2*0.05=0.4
可以看出最优组合为4+4时折扣最大。
假设用Xn表示购买第n卷数的数量,那么购买所有书数量可以用(X1,X2,X3,X4,X5)表示,而F(X1,X2,X3,X4,X5)表示最多节省钱数
简单的设为 F(Y1, Y2, Y3, Y4, Y5) 其中 Y1>= Y2, Y2>=Y3 etc
动态规划的状态转移方程就可以写成
F(Y1,Y2,Y3,Y4,Y5) = max( F(Y1-1,Y2-1,Y3-1,Y4-1,Y5-1) if y5 >= 1,
F(Y1-1,Y2-1,……..Y4-1, Y5) if y4 >=1, etc }
写成上面的原因是启发性质的, 因为我们要优先使用卷数较多的书, 尽量使卷数的种类多.
十二、编程之美 set 12 快速找出故障机器
题目
1. 所有的 ID 都出现 2 次, 只有一个例外, 找到那个例外的 ID
2. 所有的 ID 都出现两次, 只有两个例外, 找出例外的那两个
问题一:
方法一、使用计数排序(借助map)
思想:遍历整个ID列表,使用Map记录每个ID出现的次数。之后,只出现一次的ID为所求
时间复杂度O(N),空间复杂度O(N)
方法二、仍使用计数排序,但是对已经出现过两次的ID不在存储
方法三:利用异或运算(推荐使用)。将列表中的所有ID异或,之后得到的值即为所求ID。
前提是只有一个ID出现一次,若出现多次,则不适合
问题二:
情况一:丢失两个ID相等
(1)首先计算出初始未丢失之前,所有ID之和。
(2)然后计算出丢失之后的ID之和,然后(1)(2)结果进行相减操作,得到方程x+ y = a。
(3)利用丢失前后平方和之差,来与(2)进行联立,得到方程x * x + y * y = b。
(4)对两方程进行联立,即可以求出最终的结果。情况二:丢失两个ID不等
(1)对数组中所有的ID进行异或,结果为a
(2)我们找到a的二进制表示中,最低一位为1的位置b
(3)根据b位是否为1,将ID数组中的数分为两个数组,其中一个数组中的b位为1,另一个队列中的b位为0。
(注意,每个数组中,除了那个只出现一次的数外,其他数都是出现两次的,此时就可以在数组内使用异或操作)
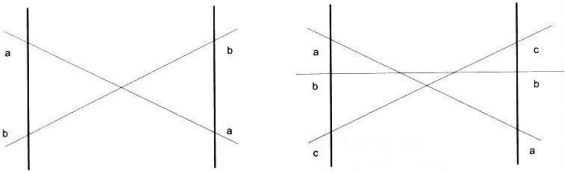
(4)然后对两个数组,分别进行异或操作,则将得到两个不为0的数字。即为所丢失的两个ID。十三、编程之美 set 13 光影切割问题
- 枚举 3 条直线的情况, 发现有规律可循
两条直线, 一个交点 -> 空间分成 4 份
三条直线, 两个交点 -> 空间分成 6 份
三条直线, 三个交点 -> 空间分成 7 份
即, 份数= 直线数+交点数+1
十四、编程之美 set 14 小飞的电梯调度算法
题目
亚洲微软研究院所在的希格玛大厦一共有6部电梯。在高峰时间,每层都有人上下,电梯每层都停。实习生小飞常常会被每层都停的电梯弄的很不耐烦,于是他提出了这样一个办法:
由于楼层并不算太高,那么在繁忙的上下班时间,每次电梯从一层往上走时,我们只允许电梯停在其中的某一层。所有乘客从一楼上电梯,到达某层后,电梯停下来,所有乘客再从这里爬楼梯到自己的目的层。在一楼的时候,每个乘客选择自己的目的层,电梯则计算出应停的楼层。
问:电梯停在哪一层楼,能够保证这次乘坐电梯的所有乘客爬楼梯的层数之和最少?
思路
假设电梯的层数是 m, 乘客人数是 n
1. 枚举, 时间复杂度是 o(mn)
2. 滚动解法. 先对 n 名乘客排序, nlogn 然后移动游标, 时间复杂度为 o(nlogn)
其实这道题目仔细分析起来就是求一组数据的中位数而已。假设两人,分别到3层楼和8层楼下,在3和8之间取一点,使得到两个点距离最小,很显然,在3和8中的每一点到3和8的距离之和都是相等的。推广到2 3 5 5 6 7 8 8 9这样一组数据,target_floor为中位数。
3、假设电梯的层数是 n, 要去第 i 层的乘客数目为 tot[i]
1. 假设在第 i 层停时, 有 X 人向上爬, Z 人不用爬, Y 人向下走, 需要走的步数之和为 F, 在这个前提下, 电梯在 i+1 层停靠. 那么 F’ = F+X+Z-Y. X = X+Z, Y = Y-TOT[i+1]
在这种数据结构下, 时间复杂度将为 o(n)
十五、编程之美 set 15 拈游戏分析(1)
题目
N 个石头排成一行, 每块石头有固定的位置和编号, 两个玩家依次取石头, 每个玩家可以取其中的任一块石头, 或者相邻的两个石头. 石头在游戏过程中不能移位, 最后将剩下的石头依次取光的玩家获胜
- 从简单的特例除法讨论
当石头的数目 N = 1,2 时, 先取者胜
当石头的数目 N = 3 时, 中间一个, 先取者胜
当石头的数目 N = 4 时, 取中间两个, 先取者胜
可以发现规律
假设 N <= i 时, 先取者胜.
当 N(N=i+1) 为奇数时, 取中间一个, 否则取中间两个, 将石子堆成相等的两堆, 两堆的数目小于 i, 对于一堆先取的胜, 两堆就是后取的胜. 得出结论, 先取的总是胜.
十六、编程之美 set 16 24点游戏
题目
输入: n1, n2, n3, n4 (1~13)
输出: 若能得到运算结果为 24, 则输出一个对应的运算表达式
如:
输入: 11, 8, 3, 5
输出: (11-8) * (3*5) = 24
思路
1. 假设不考虑括号, 4 个数, 每个数只能使用一次, 那就就对 4 个数全排列, 中间有3 个位置插入符号, 共四种符号, 共有 4!*4^3种表达式. 再加上括号, 一共 7680 种.
2. 遍历所有变量, 包括运算符, 数字, 括号是一种解法. 首先从集合中任意取出两个数, 对他们进行四则运算(A+B, A-B, B-A…) 然后再放回去即的递归解法. 这种解法效率较低, 存在较多的冗余计算.
3. 定义 Fork 函数, Fork(A,B) = {a+b, a-b, b-a…}. 假如 A 中有 m 个元素, B 中有 n 个元素, 那么 Fork(A,B) 将会有 6*m*n 个元素, 然后, 可以对这些元素进行小规模的去重, 使得返回的结果集不含重复
4. 对于单个集合, Fork(A) = Fork(A1, {A-A1}). 对于一个大小为 n 的集合 A, 其所有非空子集的个数为 2n-2(减去空集和全集)(为什么)
5. 上面的解析给出了减少返回集合冗余的方法, 但仍有重复计算. 对于重复计算部分可以设置一张表, 记录已经计算过的组合
- (1.5.2.3)编程之美 寻找发帖水王 扩展问题
- (1.5.2.4)编程之美:1的数目
- (1.5.2.5)寻找最大的K个数
- (1.5.2.11)快速寻找满足条件的两个数
游戏类
- (1.5.1.1)编程之美:让CPU占用率曲线听你指挥
- (1.5.1.2)编程之美:中国象棋将帅问题——一个变量实现多重循环
- (1.5.1.3)编程之美:一摞烙饼的排序