Python PyTorch6:卷积神经网络
1. CNN
卷积神经网络(CNN)是近年发展起来,并广泛应用于图像处理,NLP等领域的一 种多层神经网络。
如图,传统的神经网络使用全连接的策略进行极端,在处理较大的数据(如图像)时会遇到问题:权值太多,计算量太大;需要大量样本进行训练。
CNN通过局部感受野和权值共享减少了神经网络需要训练的参数个数。我们在观察一个图像的时候,不可能一眼看到图像的所有内容。这时候,CNN中隐藏层的每个神经元只和前一层的一个局部(卷积窗口,如5*5的窗口则有25个连接线)进行连接,称为局部感受野。这样,可以大大减少CNN需要训练的计算量。
2. 卷积
卷积计算时,需要使用一个卷积核,如图是一个3*3的卷积核:
这个卷积核在需要计算的矩阵上移动,每次覆盖3*3的格子时将对应位置的数字相乘再相加(如图),得到输出的3*3矩阵(特征图)。
可以设定卷积核跨越的格子数量(步长)。
3. 池化
卷积层做完卷积后,通常会在卷积后做一个池化(pooling)层。常用的池化计算包括最大池化(max-pooling)、平均池化(mean-pooling)、随机池化(stochastic pooling)等。
4. 填充
输入图像与卷积核进行卷积后的结果中损失了部分值。有时我们希望输入和输出的大小应该保持一致,为解决这个问题,可以在进行卷积操作前,对原矩阵进行边界填充(padding),也就是在矩阵的边界上填充一些值,以增加矩阵的大小,通常都用0来进行填充。
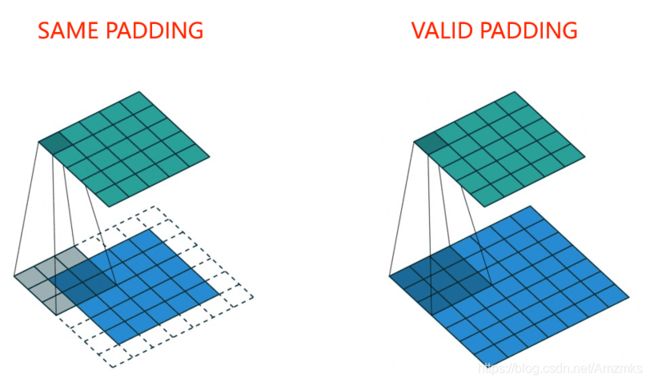
same padding: 可能将矩阵的若干圈边缘补上0,卷积窗口采样后得到一个跟原来大小相同的平面。
valid padding: 不会超出平面外部,卷积窗口采样后得到一个比原来平面小的平面。
5. LeNET-5
LeNet-5是一种用于手写体字符识别的非常高效的卷积神经网络,曾广泛用于美国银行。
例:使用卷积神经网络修改MNIST案例。
import torch
import torch.nn as nn
import torch.optim as optim
from torchvision import datasets, transforms
from torch.utils.data import DataLoader
# 下载训练集
train_dataset = datasets.MNIST(root='./',
train=True,
transform=transforms.ToTensor(),
download=True)
# 下载测试集
test_dataset = datasets.MNIST(root='./',
train=False,
transform=transforms.ToTensor(),
download=True)
# 批次大小
batch_size = 64
# 装载训练集
train_loader = DataLoader(dataset=train_dataset,
batch_size=batch_size,
shuffle=True)
# 装载测试集
test_loader = DataLoader(dataset=test_dataset,
batch_size=batch_size,
shuffle=True)
for i, data in enumerate(train_loader):
# 获得数据和对应的标签
inputs, labels = data
print(inputs.shape)
print(labels.shape)
break
# 定义网络结构
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
# 卷积层1
# Conv2d 参数1:输入通道数,黑白图片为1,彩色为3 参数2:输出通道数,生成32个特征图 参数3:5*5卷积窗口 参数4:步长1 参数5:padding补2圈0(3*3卷积窗口填充1圈0,5*5填充2圈0)
# 使用ReLU激活函数 池化窗口大小2*2,步长2
self.conv1 = nn.Sequential(nn.Conv2d(1, 32, 5, 1, 2), nn.ReLU(), nn.MaxPool2d(2, 2))
# 卷积层2 输入32个特征图 输出64个特征图
self.conv2 = nn.Sequential(nn.Conv2d(32, 64, 5, 1, 2), nn.ReLU(), nn.MaxPool2d(2, 2))
# 全连接层1 输入64*7*7(原先为28,每次池化/2),1000
self.fc1 = nn.Sequential(nn.Linear(64 * 7 * 7, 1000), nn.Dropout(p=0.4), nn.ReLU())
# 全连接层2 输出10个分类,并转化为概率
self.fc2 = nn.Sequential(nn.Linear(1000, 10), nn.Softmax(dim=1))
def forward(self, x):
# 卷积层使用4维的数据
# 批次数量64 黑白1 图片大小28*28
# ([64, 1, 28, 28])
x = self.conv1(x)
x = self.conv2(x)
# 全连接层对2维数据进行计算
x = x.view(x.size()[0], -1)
x = self.fc1(x)
x = self.fc2(x)
return x
LR = 0.0003
# 定义模型
model = Net()
# 定义代价函数
entropy_loss = nn.CrossEntropyLoss()
# 定义优化器
optimizer = optim.Adam(model.parameters(), LR)
def train():
model.train()
for i, data in enumerate(train_loader):
# 获得数据和对应的标签
inputs, labels = data
# 获得模型预测结果,(64,10)
out = model(inputs)
# 交叉熵代价函数out(batch,C),labels(batch)
loss = entropy_loss(out, labels)
# 梯度清0
optimizer.zero_grad()
# 计算梯度
loss.backward()
# 修改权值
optimizer.step()
def test():
model.eval()
correct = 0
for i, data in enumerate(test_loader):
# 获得数据和对应的标签
inputs, labels = data
# 获得模型预测结果
out = model(inputs)
# 获得最大值,以及最大值所在的位置
_, predicted = torch.max(out, 1)
# 预测正确的数量
correct += (predicted == labels).sum()
print("Test acc: {0}".format(correct.item() / len(test_dataset)))
correct = 0
for i, data in enumerate(train_loader):
# 获得数据和对应的标签
inputs, labels = data
# 获得模型预测结果
out = model(inputs)
# 获得最大值,以及最大值所在的位置
_, predicted = torch.max(out, 1)
# 预测正确的数量
correct += (predicted == labels).sum()
print("Train acc: {0}".format(correct.item() / len(train_dataset)))
for epoch in range(0, 10):
print('epoch:', epoch)
train()
test()
输出:
torch.Size([64, 1, 28, 28])
torch.Size([64])
epoch: 0
Test acc: 0.9764
Train acc: 0.9738833333333333
epoch: 1
Test acc: 0.9813
Train acc: 0.9808166666666667
epoch: 2
Test acc: 0.9838
Train acc: 0.9848
epoch: 3
Test acc: 0.9874
Train acc: 0.9889
epoch: 4
Test acc: 0.9886
Train acc: 0.98935
epoch: 5
Test acc: 0.9904
Train acc: 0.9917333333333334
epoch: 6
Test acc: 0.9874
Train acc: 0.9913666666666666
epoch: 7
Test acc: 0.9901
Train acc: 0.9923166666666666
epoch: 8
Test acc: 0.9894
Train acc: 0.9933
epoch: 9
Test acc: 0.9917
Train acc: 0.9951