Logistic回归-模型·损失函数·参数更新

理解Logistic回归首先要了解线性回归(http://blog.csdn.net/u013917439/article/details/77481216)。Linear Regression: h=WTX

---

 训练集共m个样本，第i个样本 (x(i),y(i)),x(i)=(x(i)1,x(i)2,...,x(i)d)T ，即有d维特征。为了表示方便，将偏置b统一到权重W里。 W=(w0,w1,...,wd),w0=b 。

1 逻辑回归

 Logistic回归将线性回归的结果输入到sigmoid函数函数中，得到一个0-1之间的数值，可用与分类。当结果大于 0.5时是正类，小于0.5时是负类。
sigmoid函数，也叫Logistic函数：

g(t)=11+e−t

图像如下：

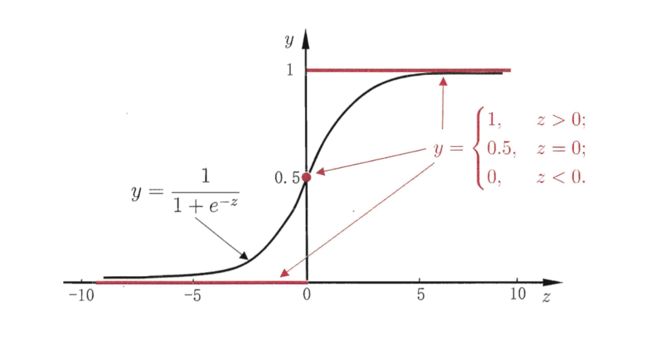
Logistic回归模型：

• 假设函数 Hypothesis:hw(X)=11+e−WTX

  hw(X)=g(WTX)
  g(z)=11+e−z
  z=WTX

  • 参数　　　　 Parameters:w
  • 损失函数　　 CostFunction:J(w)=−1m∑mi=1[y(i)log(hw(x(i)))+(1−y(i))log(1−hw(x(i)))]
  • 优化目标　　 Goal:minimizeJ(w)

2 模型函数

 为什么将线性回归的结果输入到sigmoid函数中去做分类呢？
 线性回归本身是预测连续值，是用于对线性数据进行拟合。输入特征X，输出的预测值 y∈R ，是实数集合。而二分类任务输入特征X后，输出 y∈0,1 。
 怎样把实数集合映射到0,1？ sigmoid函数：定义域R，值域（0，1)，则 hw(X)=g(WTX) 的输出是0-1之间的数值，输出的是该样本为正类的概率。再用概率值判断所属类别。

p(y=1|x,w)=hw(x(i))
p(y=0|x,w)=1−hw(x(i))

• 对数几率
   将 hw(x(i)) 视为样本作为正例的概率，则 1−hw(x(i)) 是该样本为反例的概率，两者的比值称为“几率“(odds)，反应了 x(i) 作为正例的相对可能性。
  

  odds=hw(x(i))1−hw(x(i))
  
  对几率取对数即得到对数几率，将 hw(X)=g(WTX) 带入，求得
  
  logodds=loghw(x(i))1−hw(x(i))=WTX
  
  则 hw(x(i)) 实际上是在用线性回归的预测结果去逼近真实标记的对数几率，即对对数几率进行线性回归预测。所以逻辑回归也称为对数几率回归。

• 决策边界Decision Boundary

  正类 <=> hw(X)>0.5<=>WTX>0
  负类 <=> hw(X)<0.5<=>WTX<0

2 损失函数

2.1 损失函数直观理解

整个样本集的损失为样本集中每个样本预测值与真实值的误差的平均值。

J(w)=−1m∑i=1mCost(hw(x(i))−y(i))

那么怎么度量每个样本预测值与真实值的误差呢？ Cost(hw(x),y) 计算公式和图像如下

{Cost(hw(x),y)=−log(hw(x))ify=1Cost(hw(x),y)=−log(1−hw(x))ify=0

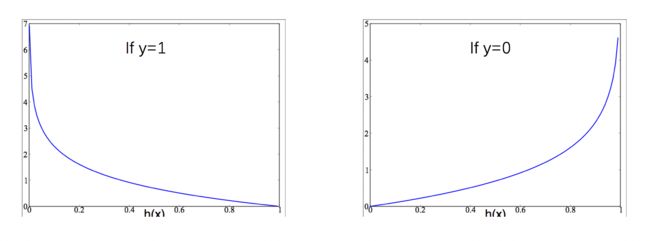
可以看出：

• 当 y=1 时，若 hw(x)=1Cost(hw(x),y)=0 ，若 hw(x)=0Cost(hw(x),y)= 无穷大。 hw(x) 越接近与1损失值越小，越接近于0损失值越大。
• 当 y=0 时，若 hw(x)=0Cost(hw(x),y)=0 ，若 hw(x)=1Cost(hw(x),y)= 无穷大。 hw(x) 越接近与0损失值越小，越接近于1损失值越大。

2.2 由最大似然估计求解参数

 由 p(y=1|x,w)=hw(x(i)) p(y=0|x,w)=1−hw(x(i)) 结合在一起，正类负类都可以表达，每一个样本 (x(i),y(i)) 出现的概率为

p(y(i)|x(i),w)=[hw(x(i))y(i)]∗[(1−hw(x(i)))1−y(i)]

 各个样本之间相互独立，对于整个样本集 D=(x(1),y(1)),(x(2),y(2)),...,(x(m),y(m)) ,得到该样本集的概率为：

p(D)===p(y(1)|x(1),w)∗p(y(2)|x(2),w)∗...∗p(y(m)|x(m),w)∏i=1mp(y(i)|x(i),w)∏i=1m[hw(x(i))y(i)]∗[(1−hw(x(i)))1−y(i)]

 这个概率反应了，当参数是w时，得到这组样本的概率，即为似然函数L(w)=p(D)。最大似然估计是通过观测样本寻找一组参数，使这组样本同时出现的概率最大，即寻找使似然函数取最大值的参数。
将似然函数取对数得到对数似然函数：

log(L(w))===log[p(y(1)|x(1),w)∗p(y(2)|x(2),w)∗...∗p(y(m)|x(m),w)]∑i=1mlog(p(y(i)|x(i),w))∑i=1m[y(i)log(hw(x(i)))+(1−y(i))log(1−hw(x(i)))]

 要求得 max[log(L(w))] 时的参数值，由上式对 wj 求偏导，得到d+1个方程，问题转化为解这个d+1方程形成的方程组。然而上述方程比较复杂，无法直接解出参数值，可以用牛顿法，或梯度上升法等优化方法求解。
 若采用梯度下降法，则优化目标为 min[−log(L(w))] ，等价于下面的公式，与前面的损失函数一致。

minJ(w)=min−1m∑i=1m[y(i)log(hw(x(i)))+(1−y(i))log(1−hw(x(i)))]

3 梯度下降参数更新

损失函数： J(w)=−1m∑mi=1[y(i)log(hw(x(i)))+(1−y(i))log(1−hw(x(i)))]
优化目标： minimizeJ(w)
梯度下降参数更新过程：
步骤：

1.初始化 w1,w2...,wd
2.同步更新所有参数，使 J(w,b) 不断减小。（ α 是学习率）
　　　　　 wj:=wj−α∂∂wjJ(w,b)(j=0,...,d)
3.重复步骤2直至收敛

• 
  
• 推导：
  计算偏导数
  因为
  J(w)=−1m∑i=1m[y(i)log(hw(x(i)))+(1−y(i))log(1−hw(x(i)))]
  
  
  hw(x)=g(WTx)g(z)=11+e−z
  
  则
  
  J(w)=−1m∑i=1m[y(i)log(g(WTx))+(1−y(i))log(1−g(WTx))]
  
  
  g(z)′====e−z(1+e−z)211+e−ze−z1+e−z11+e−z1+e−z−11+e−zg(z)(1−g(z))
  
  所以
  
  ∂∂wJ(w)====−1m∑i=1m[y(i)1g(WTx(i))+(1−y(i))11−g(WTx(i))]∂∂wg(WTx(i))−1m∑i=1my(i)(1−g(WTx(i)))+(1−y(i))g(WTx(i))g(WTx(i))(1−g(WTx(i))g(WTx(i))(1−g(WTx(i))∂∂w(WTx(i))−1m∑i=1m(y(i)−g(WTx(i)))x(i)1m∑i=1m(hw(x(i))−y(i))x(i)
  
  则参数更新公式为
  

wj:=wj−α1m∑mi=1(h(x(i))−y(i))x(i)j （ 与线性回归参数更新公式的形式相同，但 h(x(i)) 不同。）

参考资料：

1.Andrew Ng的Machine Learning课程
2.《机器学习》周志华