国科大《模式识别》课程总结
《模式识别》课程总结
- 1、贝叶斯决策理论
-
- 1.1基本理论
- 1.2高斯分布:
- 1.3高斯密度下的判别函数:
- 1.4分类错误率:
- 1.5离散变量贝叶斯决策
- 2、参数估计
-
- 2.1最大似然估计
- 2.2贝叶斯估计
- 3、半参数方法
-
- 3.1期望最大化算法(EM)
- 3.2隐马尔可夫模型(HMM)
- 4、非参数方法
-
- 4.1帕森窗
- 4.2K近邻估计
- 4.3距离度量:
- 5、线性判别函数
-
- 5.1线性判别
- 5.2广义线性判别
- 5.3感知准则函数
- 5.4最小均方误差(MSE)准则函数
- 5.5多类线性判别函数
- 6、人工神经网络
-
- 6.1简要介绍
- 6.2前馈神经网络(感知机)
- 6.3径向基函数网络
- 6.4Hopfield网络
- 6.5玻尔兹曼机(BM)
- 6.6深度信念网络、深度玻尔兹曼机
- 6.7自组织映射(SOM)
- 6.8自编码器(Autoencoder)
- 7、特征提取
-
- 7.1 语音特征提取
- 7.2文本特征提取
- 7.3视觉特征提取
- 8、维数缩减
-
- 8.1线性维数缩减
-
- 8.1.1 主成分分析(PCA)
- 8.1.2 线性判别分析(LDA)
- 8.2非线性维数缩减
-
- 8.2.1 多维缩放(MDS)
- 8.2.2流形学习
- 9、特征选择
-
- 9.1评价判据
- 9.2子集搜索
- 10、模型选择
- 11、数据聚类
-
- 11.1 k-means聚类
- 11.2 高斯混合模型
- 11.3 分级聚类
- 11.4 谱聚类(K-means in spectrum space)
- 11.5 核聚类
- 12、支持向量机与核方法
- 13、决策树
判别模型:由数据直接学习决策函数或条件概率分布,输入X即输出Y。学习不同样本之间的区别。
生成模型:通过学习联合概率分布计算条件概率分布,学习到的是输入X与输出Y的关系。学习数据分布的内在规律。分为三种方法:1)参数法、2)半参数法、3)非参数法

1、贝叶斯决策理论
1.1基本理论
后验概率:
p ( ω i ∣ x ) = p ( x ∣ ω i ) p ( ω i ) p ( x ) , ∑ i = 1 c p ( ω i ∣ x ) = 1 p(\omega_i |x)=\frac{p(x|\omega_i)p(\omega_i)}{p(x)},\quad \sum_{i=1}^cp(\omega_i|x)=1 p(ωi∣x)=p(x)p(x∣ωi)p(ωi),i=1∑cp(ωi∣x)=1
最小错误率决策: p ( e r r o e ∣ x ) = m i n [ p ( ω 1 ∣ x ) , p ( ω 2 ∣ x ) ] p(erroe|x)=min[p(\omega_1|x),p(\omega_2|x)] p(erroe∣x)=min[p(ω1∣x),p(ω2∣x)],分类时基于最大后验概率。
最小风险决策:引入决策代价 λ i j = λ ( α i ∣ ω j ) \lambda_{ij}=\lambda(\alpha_i|\omega_j) λij=λ(αi∣ωj),即将真实j类错分为i类的代价。此时条件风险为:
R ( α i ∣ x ) = ∑ j = 1 c λ ( α i ∣ ω j ) p ( ω j ∣ x ) R = ∫ R ( α ( x ) ∣ x ) p ( x ) d x R(\alpha_i|x)=\sum_{j=1}^c\lambda(\alpha_i|\omega_j)p(\omega_j|x)\\ R=\int R(\alpha(x)|x)p(x)dx R(αi∣x)=j=1∑cλ(αi∣ωj)p(ωj∣x)R=∫R(α(x)∣x)p(x)dx
对于二分类问题,有
R ( α 1 ∣ x ) = λ 11 p ( ω 1 ∣ x ) + λ 12 p ( ω 2 ∣ x ) R ( α 2 ∣ x ) = λ 21 p ( ω 1 ∣ x ) + λ 22 p ( ω 2 ∣ x ) R(\alpha_1|x)=\lambda_{11}p(\omega_1|x)+\lambda_{12}p(\omega_2|x)\\ R(\alpha_2|x)=\lambda_{21}p(\omega_1|x)+\lambda_{22}p(\omega_2|x) R(α1∣x)=λ11p(ω1∣x)+λ12p(ω2∣x)R(α2∣x)=λ21p(ω1∣x)+λ22p(ω2∣x)
最小错误率分类:对应于决策代价为0-1损失。此时
R ( α i ∣ x ) = ∑ j = 1 c λ ( α i ∣ ω i ) p ( ω j ∣ x ) = ∑ j ≠ i p ( ω j ∣ x ) = 1 − p ( ω i ∣ x ) \begin{aligned}R(\alpha_i|x)&=\sum_{j=1}^c\lambda(\alpha_i|\omega_i)p(\omega_j|x)\\ &=\sum_{j\ne i}p(\omega_j|x)\\ &=1-p(\omega_i|x) \end{aligned} R(αi∣x)=j=1∑cλ(αi∣ωi)p(ωj∣x)=j=i∑p(ωj∣x)=1−p(ωi∣x)带拒识的决策:决策代价为:
λ ( α i ∣ ω j ) = { 0 i = j λ s i ≠ j λ r r e j e c t \begin{aligned}\lambda (\alpha_i|\omega_j)=\begin{cases} 0 & i=j \\ \lambda_s & i\ne j \\ \lambda_r & reject \end{cases}\end{aligned} λ(αi∣ωj)=⎩ ⎨ ⎧0λsλri=ji=jreject则条件风险为:
R i ( x ) = { λ s [ 1 − p ( ω i ∣ x ) ] i = 1 , 2... c λ r r e j e c t \begin{aligned}R_i(\rm x)=\begin{cases} \lambda_s[1-p(\omega_i|\rm x)] & i=1,2...c \\ \lambda_r & reject \end{cases} \end{aligned} Ri(x)={λs[1−p(ωi∣x)]λri=1,2...creject 开放集分类贝叶斯决策: c个类中再加一个未知类别,假设条件概率 p ( x ∣ ω c + 1 ) = ρ p(\rm x|\omega_{c+1})=\rho p(x∣ωc+1)=ρ,是一个很小的数。
判别函数: a r g m a x g i ( x ) argmax \;g_i(x) argmaxgi(x),可以是最大化后验概率或最小化条件风险。
决策面: 特征空间中判别函数相等的点的合集。
类条件密度估计:
贝叶斯决策的核心是类条件概率密度的估计,可以分为参数法、半参数法和非参数法三类方法。
1、参数法:假定概率密度函数的形式为: p ( x ∣ ω i ) = p ( x ∣ θ i ) p(\rm x|\omega_i)=p(\rm x|\theta_i) p(x∣ωi)=p(x∣θi),函数可以服从高斯分布、伽马分布、伯努利分布。参数估计方法有:最大似然估计、贝叶斯估计。
2、半参数法:近似任意概率分布,即高斯混合模型(GMM),估计方法为期望最大化(EM)。
3、非参数法:可以表示任意概率分布,没有函数形式,如帕森窗、K近邻。
1.2高斯分布:
在给定均值和方差的所有分布中,正态分布的熵最大,且根据中心极限定理,大量独立随机变量之和趋近于正态分布。
p ( x ) = 1 2 π σ e x p [ − 1 2 ( x − μ σ ) 2 ] p(x)=\frac{1}{\sqrt{2\pi}\sigma}exp\left[-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2\right] p(x)=2πσ1exp[−21(σx−μ)2]多变量:
p ( x ) = 1 ( 2 π ) d / 2 ∣ Σ ∣ 1 / 2 e x p [ − 1 2 ( x − μ ) t Σ − 1 ( x − μ ) ] p(x)=\frac{1}{(2\pi)^{d/2}|\Sigma|^{1/2}}exp\left[-\frac{1}{2}(x-\mu)^t\Sigma^{-1}(x-\mu)\right] p(x)=(2π)d/2∣Σ∣1/21exp[−21(x−μ)tΣ−1(x−μ)]如果 x i x_i xi与 x j x_j xj相互独立,则协方差矩阵退化为对角矩阵。协方差矩阵刻画的等密度点轨迹是一个超椭球面,越靠近中心密度越大,且同一椭球面上的概率密度相等(马氏距离相等)。
协方差矩阵的性质:
1、做特征值分解: Σ = Φ Λ Φ T \Sigma=\Phi \Lambda \Phi^T Σ=ΦΛΦT,其中 Φ \Phi Φ是单位正交矩阵,应用:PCA降维。
2、线性变换:
对角化; A = Φ A=\Phi A=Φ, A t Σ A = Λ A^t\Sigma A=\Lambda AtΣA=Λ,将坐标轴旋转。
白化变换: A w = Φ Λ − 1 / 2 A_w=\Phi \Lambda^{-1/2} Aw=ΦΛ−1/2, A w t Σ A w = I A_w^t\Sigma A_w=I AwtΣAw=I,变换为单位矩阵。
1.3高斯密度下的判别函数:
g i ( x ) = l n p ( x ∣ ω i ) + l n p ( ω i ) p ( x ∣ ω i ) = 1 ( 2 π ) d / 2 ∣ Σ i ∣ 1 / 2 e x p [ − 1 2 ( x − μ i ) t Σ i − 1 ( x − μ i ) ] g i ( x ) = − 1 2 ( x − μ i ) t Σ i − 1 ( x − μ i ) − 1 2 l n 2 π − 1 2 l n ∣ Σ i ∣ + l n p ( ω i ) \begin{aligned} g_i(\rm x)&=ln\;p(\rm x|\omega_i)+ln\;p(\omega_i)\\ p(\rm x|\omega_i)&=\frac{1}{(2\pi)^{d/2}|\Sigma_i|^{1/2}}exp\left[-\frac{1}{2}(x-\mu_i)^t\Sigma_i^{-1}(x-\mu_i)\right]\\ g_i(\rm x)&=-\frac{1}{2}(x-\mu_i)^t\Sigma_i^{-1}(x-\mu_i)-\frac{1}{2}ln\;2\pi-\frac{1}{2}ln\;|\Sigma_i|+ln\;p(\omega_i) \end{aligned} gi(x)p(x∣ωi)gi(x)=lnp(x∣ωi)+lnp(ωi)=(2π)d/2∣Σi∣1/21exp[−21(x−μi)tΣi−1(x−μi)]=−21(x−μi)tΣi−1(x−μi)−21ln2π−21ln∣Σi∣+lnp(ωi) 是一个二次函数,讨论以下类别:
1、当 Σ i = ∣ σ 2 ∣ \Sigma_i=|\sigma^2| Σi=∣σ2∣时,即方差相等,协方差为0,带入并忽略与类别无关项,得到线性判别函数:
g i ( x ) = − 1 2 σ 2 ( − 2 μ i t x + μ i t μ i ) + l n p ( ω i ) = w i t x + b i g_i(\rm x)=-\frac{1}{2\sigma^2}(-2\mu_i^t\rm x+\mu_i^t\mu_i)+ln\;p(\omega_i)=w_i^tx+b_i gi(x)=−2σ21(−2μitx+μitμi)+lnp(ωi)=witx+bi二分类决策面: g i ( x ) = g j ( x ) g_i(\rm x)=g_j(x) gi(x)=gj(x)可以推出 w t ( x − x 0 ) = 0 \rm w^t(x-x_0)=0 wt(x−x0)=0,其中 w = μ i − μ j \rm w=\mu_i-\mu_j w=μi−μj,
x 0 = 1 2 ( μ i = μ j ) − σ 2 ∣ ∣ μ i − μ j ∣ ∣ 2 l n p ( ω i ) p ( ω j ) ( μ i − μ j ) \rm x_0=\frac{1}{2}(\mu_i=\mu_j)-\frac{\sigma^2}{||\mu_i-\mu_j||^2}ln\frac{p(\omega_i)}{p(\omega_j)}(\mu_i-\mu_j) x0=21(μi=μj)−∣∣μi−μj∣∣2σ2lnp(ωj)p(ωi)(μi−μj)可以看出当先验概率不同时,分界面向先验概率小的一侧移动。决策面与 μ i − μ j \mu_i-\mu_j μi−μj垂直。
2、所有类别共享协方差矩阵 Σ i = Σ \Sigma_i=\Sigma Σi=Σ,此时决策函数变为:
g i ( x ) = − 1 2 ( x − μ i ) t Σ − 1 ( x − μ i ) + l n p ( ω i ) g_i(\rm x)=-\frac{1}{2}(x-\mu_i)^t\Sigma^{-1}(x-\mu_i)+ln\;p(\omega_i) gi(x)=−21(x−μi)tΣ−1(x−μi)+lnp(ωi)二分类决策面: g i ( x ) = g j ( x ) g_i(\rm x)=g_j(x) gi(x)=gj(x)可以推出 w t ( x − x 0 ) = 0 \rm w^t(x-x_0)=0 wt(x−x0)=0,其中 w = Σ − 1 ( μ i − μ j ) \rm w=\Sigma^{-1} (\mu_i-\mu_j) w=Σ−1(μi−μj),
x 0 = 1 2 ( μ i = μ j ) − 1 ( μ i − μ j ) t Σ − 1 ( μ i − μ j ) l n p ( ω i ) p ( ω j ) ( μ i − μ j ) \rm x_0=\frac{1}{2}(\mu_i=\mu_j)-\frac{1}{(\mu_i-\mu_j)^t\Sigma^{-1}(\mu_i-\mu_j)}ln\frac{p(\omega_i)}{p(\omega_j)}(\mu_i-\mu_j) x0=21(μi=μj)−(μi−μj)tΣ−1(μi−μj)1lnp(ωj)p(ωi)(μi−μj)可以看出当先验概率不同时,分界面向先验概率小的一侧移动。
3、 Σ \Sigma Σ为任意对称矩阵。此时 g i ( x ) = x t W i x + w i t x + ω i 0 g_i(\rm x)=x^tW_ix+w_i^tx+\omega_{i0} gi(x)=xtWix+witx+ωi0,其中有 W i = − 1 2 Σ i − 1 W_i=-\frac{1}{2}\Sigma_i^{-1} Wi=−21Σi−1, w i = Σ i − 1 μ i w_i=\Sigma_i^{-1}\mu_i wi=Σi−1μi, ω i 0 = − 1 2 μ i t Σ − 1 μ i − 1 2 l n ∣ Σ i ∣ + l n p ( ω i ) \rm \omega_{i0}=-\frac{1}{2}\mu_i^t\Sigma^{-1}\mu_i-\frac{1}{2}ln\;|\Sigma_i|+ln\;p(\omega_i) ωi0=−21μitΣ−1μi−21ln∣Σi∣+lnp(ωi),其二类决策面是一个超曲面。
1.4分类错误率:
2类的情况
P ( e r r o r ) = P ( x ∈ R 2 , ω 1 ) + P ( x ∈ R 1 , ω 2 ) = P ( x ∈ R 2 ∣ ω 1 ) P ( ω 1 ) + P ( x ∈ R 1 ∣ ω 2 ) P ( ω 2 ) = ∫ R 2 p ( x ∣ ω 1 ) P ( ω 1 ) d x + ∫ R 1 p ( x ∣ ω 2 ) P ( ω 2 ) d x \begin{aligned}P(error)&=P(x\in R_2,\omega_1)+P(x\in R_1,\omega_2)\\ &=P(x\in R_2|\omega_1)P(\omega_1)+P(x\in R_1|\omega_2)P(\omega_2)\\ &=\int_{R_2}p(x|\omega_1)P(\omega_1)dx+\int_{R_1}p(x|\omega_2)P(\omega_2)dx \end{aligned} P(error)=P(x∈R2,ω1)+P(x∈R1,ω2)=P(x∈R2∣ω1)P(ω1)+P(x∈R1∣ω2)P(ω2)=∫R2p(x∣ω1)P(ω1)dx+∫R1p(x∣ω2)P(ω2)dx其中 ∫ R 2 \int_{R_2} ∫R2表示为对第二类决策区域做积分,见下图:

当似然度相等时,即联合概率相等时,分类错误率最小。推广到多类:
P ( e r r o r ) = ∑ i = 1 c ∫ R i p ( x ∣ ω i ) P ( ω i ) d x P(error)=\rm \sum_{i=1}^c\int_{R_i}p(x|\omega_i)P(\omega_i)dx P(error)=i=1∑c∫Rip(x∣ωi)P(ωi)dx(0-1loss)时最大后验概率决策的错误率:
P ( c o r r e c t ) = ∫ x m a x i p ( x ∣ ω i ) P ( ω i ) d x = ∫ x m a x i P ( ω i ∣ x ) p ( x ) d x P ( e r r o r ) = ∫ x [ 1 − m a x i P ( ω i ∣ x ) ] p ( x ) d x \begin{aligned} P(correct)&=\int_x\underset{i}{max} \;p(x|\omega_i)P(\omega_i)dx\\ &=\int_x\underset{i}{max} \;P(\omega_i|x)p(x)dx\\ P(error)&=\int_x\left[1-\underset{i}{max} \;P(\omega_i|x)\right]p(x)dx \end{aligned} P(correct)P(error)=∫ximaxp(x∣ωi)P(ωi)dx=∫ximaxP(ωi∣x)p(x)dx=∫x[1−imaxP(ωi∣x)]p(x)dx贝叶斯分类器是最优的分类器,但通常概率密度、条件风险无法准确估计。
1.5离散变量贝叶斯决策
独立二值特征;
p ( x ) = p ( x 1 x 2 . . . x d ) = ∏ i = 1 d p ( x i ) , x i = 0 o r 1 p i = P r o b ( x i = 1 ∣ ω 1 ) , q i = P r o b ( x i = 1 ∣ ω 2 ) p(x)=p(x_1x_2...x_d)=\prod_{i=1}^{d}p(x_i),\quad x_i=0\,or\,1 \\ p_i=Prob(x_i=1|\omega_1),\quad q_i=Prob(x_i=1|\omega_2) p(x)=p(x1x2...xd)=i=1∏dp(xi),xi=0or1pi=Prob(xi=1∣ω1),qi=Prob(xi=1∣ω2)则:
P ( x ∣ ω 1 ) = ∏ i = 1 d p i x i ( 1 − p i ) 1 − x i P ( x ∣ ω 2 ) = ∏ i = 1 d q i x i ( 1 − q i ) 1 − x i P(x|\omega_1)=\prod_{i=1}^{d}p_i^{x_i}(1-p_i)^{1-x_i}\\ P(x|\omega_2)=\prod_{i=1}^{d}q_i^{x_i}(1-q_i)^{1-x_i} P(x∣ω1)=i=1∏dpixi(1−pi)1−xiP(x∣ω2)=i=1∏dqixi(1−qi)1−xi此时判别函数为
g ( x ) = l o g p ( x ∣ ω 1 ) P ( ω 1 ) p ( x ∣ ω 2 ) P ( ω 2 ) \rm g(x)=log\frac{p(x|\omega_1)P(\omega_1)}{p(x|\omega_2)P(\omega_2)} g(x)=logp(x∣ω2)P(ω2)p(x∣ω1)P(ω1)展开后是一个线性判别函数 g ( x ) = ∑ i = 1 d ω i x i + ω 0 \rm g(x)=\sum_{i=1}^d\omega_ix_i+\omega_0 g(x)=∑i=1dωixi+ω0,其中 ω i = l n p i ( 1 − q i ) q i ( 1 − p i ) i = 1 , . . . , d \omega_i=ln\frac{p_i(1-q_i)}{q_i(1-p_i)}\,i=1,...,d ωi=lnqi(1−pi)pi(1−qi)i=1,...,d可以看出,当 p i = q i p_i=q_i pi=qi时,两类在第i个特征维度上没有区分性。
2、参数估计
两个方法:
1)最大似然估计:假设参数为一个确定值,似然度最大时为最优估计。
2)贝叶斯估计:假设参数为随机变量,估计其分布。
2.1最大似然估计
p ( D ∣ θ ) = ∏ k = 1 n p ( x k ∣ θ ) ⟷ ∑ k = 1 n l n p ( x k ∣ θ ) m a x θ p ( D ∣ θ ) ⟷ ▽ θ p ( D ∣ θ ) = 0 p(D|\theta)=\prod_{k=1}^{n}p(x_k|\theta)\longleftrightarrow \sum_{k=1}^nln\;p(x_k|\theta)\\ \underset{\theta}{max}p(D|\theta)\longleftrightarrow \bigtriangledown_\theta p(D|\theta)=0 p(D∣θ)=k=1∏np(xk∣θ)⟷k=1∑nlnp(xk∣θ)θmaxp(D∣θ)⟷▽θp(D∣θ)=0 均值和方差未知的高斯参数估计: θ 1 = μ , θ 2 = σ 2 \theta_1=\mu,\; \theta_2=\sigma^2 θ1=μ,θ2=σ2:
l n p ( x k ∣ θ ) = − 1 2 l n ( 2 π θ 2 ) − 1 2 θ 2 ( x k − θ 1 ) 2 ▽ θ l n p ( x k ∣ θ ) = [ 1 θ 2 ( x k − θ 1 ) − 1 2 θ 2 + ( x k − θ 1 ) 2 2 θ 2 2 ] = [ 0 0 ] ln\;p(x_k|\theta)=-\frac{1}{2}ln(2\pi\theta_2)-\frac{1}{2\theta_2}(x_k-\theta_1)^2\\ \bigtriangledown_\theta\;ln\;p(x_k|\theta)=\begin{bmatrix} \frac{1}{\theta_2}(x_k-\theta_1)\\ -\frac{1}{2\theta_2}+\frac{(x_k-\theta_1)^2}{2\theta_2^2} \end{bmatrix}=\begin{bmatrix} 0\\ 0 \end{bmatrix} lnp(xk∣θ)=−21ln(2πθ2)−2θ21(xk−θ1)2▽θlnp(xk∣θ)=[θ21(xk−θ1)−2θ21+2θ22(xk−θ1)2]=[00]可以解得:
μ ^ = 1 n ∑ k = 1 n x k σ ^ 2 = 1 n ∑ k = 1 n ( x k − μ ^ ) 2 \hat \mu=\frac{1}{n}\sum_{k=1}^{n}x_k\\ \hat \sigma^2=\frac{1}{n}\sum_{k=1}^n(x_k-\hat \mu)^2 μ^=n1k=1∑nxkσ^2=n1k=1∑n(xk−μ^)2推广到高维情况时:
μ ^ = 1 n ∑ k = 1 n x k Σ ^ = 1 n ∑ k = 1 n ( x k − μ ^ ) ( x k − μ ^ ) t \hat \mu=\frac{1}{n}\sum_{k=1}^{n}x_k\\ \hat \Sigma=\frac{1}{n}\sum_{k=1}^n(x_k-\hat \mu)(x_k-\hat \mu)^t μ^=n1k=1∑nxkΣ^=n1k=1∑n(xk−μ^)(xk−μ^)t值得注意的是,最大似然估计是有偏估计。
2.2贝叶斯估计
基本条件:知道密度函数 p ( x ∣ θ ) p(x|\theta) p(x∣θ)的形式,知道先验参数分布 p ( θ ) p(\theta) p(θ)(如果不知道,可以假设为高斯分布),拥有n个样本的数据集D,样本相互独立。
步骤:估计后验参数分布:
p ( θ ∣ D ) = p ( D ∣ θ ) p ( θ ) ∫ p ( D ∣ θ ) p ( θ ) d θ p ( D ∣ θ ) = ∏ k = 1 n p ( x k ∣ θ ) p(\theta|D)=\frac{p(D|\theta)p(\theta)}{\int p(D|\theta)p(\theta)d\theta}\quad p(D|\theta)=\prod_{k=1}^{n}p(x_k|\theta) p(θ∣D)=∫p(D∣θ)p(θ)dθp(D∣θ)p(θ)p(D∣θ)=k=1∏np(xk∣θ)估计后验数据分布:
p ( x ∣ D ) = ∫ p ( x , θ ∣ D ) d θ = ∫ p ( x ∣ θ ) p ( θ ∣ D ) d θ p(x|D)=\int p(x,\theta|D)d\theta=\int p(x|\theta)p(\theta|D)d\theta p(x∣D)=∫p(x,θ∣D)dθ=∫p(x∣θ)p(θ∣D)dθ 例子: 在一维高斯分布下估计 p ( μ ∣ D ) p(\mu|D) p(μ∣D):
假设参数条件下的密度函数服从高斯分布 p ( x ∣ μ ) ∼ N ( μ , σ 2 ) p(x|\mu)\sim N(\mu, \sigma^2) p(x∣μ)∼N(μ,σ2)。
假设参数也是服从于高斯分布 p ( μ ) ∼ N ( μ 0 , σ 0 2 ) p(\mu)\sim N(\mu_0, \sigma_0^2) p(μ)∼N(μ0,σ02)
则参数的后验分布为:
p ( μ ∣ D ) = p ( D ∣ μ ) p ( μ ) ∫ p ( D ∣ μ ) p ( μ ) d μ = α ∏ k = 1 n p ( x k ∣ μ ) p ( μ ) p(\mu|D)=\frac{p(D|\mu)p(\mu)}{\int p(D|\mu)p(\mu)d\mu}=\alpha \prod_{k=1}^{n}p(x_k|\mu)p(\mu) p(μ∣D)=∫p(D∣μ)p(μ)dμp(D∣μ)p(μ)=αk=1∏np(xk∣μ)p(μ)将高斯分布方程带入可以得到:
p ( μ ∣ D ) = α ′ ′ e x p { − 1 2 [ ( n σ 2 + 1 σ 0 2 ) μ 2 − 2 ( 1 σ 2 ∑ k = 1 n x k + μ 0 σ o 2 ) μ ] } p(\mu|D)=\alpha'' exp\left\{-\frac{1}{2}\left[(\frac{n}{\sigma^2}+\frac{1}{\sigma_0^2})\mu^2-2(\frac{1}{\sigma^2}\sum_{k=1}^n x_k+\frac{\mu_0}{\sigma_o^2})\mu \right]\right\} p(μ∣D)=α′′exp{−21[(σ2n+σ021)μ2−2(σ21k=1∑nxk+σo2μ0)μ]} 可以看到其先验分布和后验分布是同类型的分布,即共轭先验。将其改为标准高斯分布形式,即:
p ( μ ∣ D ) = 1 2 π σ n e x p [ − 1 2 ( μ − μ n σ n ) 2 ] p(\mu|D)=\frac{1}{\sqrt{2\pi}\sigma_n}exp\left[-\frac{1}{2}(\frac{\mu-\mu_n}{\sigma_n})^2\right] p(μ∣D)=2πσn1exp[−21(σnμ−μn)2]其中:
σ n 2 = σ 0 2 σ 2 n σ 0 2 + σ 2 μ n = n σ 0 2 n σ 0 2 + σ 2 μ ^ n + σ 2 n σ 0 2 + σ 2 μ 0 \sigma_n^2=\frac{\sigma_0^2\sigma^2}{n\sigma_0^2+\sigma^2}\qquad \mu_n=\frac{n\sigma_0^2}{n\sigma_0^2+\sigma^2}\hat \mu_n+\frac{\sigma^2}{n\sigma_0^2+\sigma^2}\mu_0 σn2=nσ02+σ2σ02σ2μn=nσ02+σ2nσ02μ^n+nσ02+σ2σ2μ0 μ ^ n \hat \mu_n μ^n是最大似然估计。可以看出,当n增大时, μ n ⟶ μ ^ n , σ n 2 ⟶ σ / n \mu_n\longrightarrow \hat \mu_n,\sigma_n^2\longrightarrow \sigma/n μn⟶μ^n,σn2⟶σ/n。
后验数据分布:
p ( x ∣ D ) = ∫ p ( x ∣ μ ) p ( μ ∣ D ) d μ = 1 2 π σ σ n e x p [ − 1 2 ( x − μ n ) 2 σ 2 + σ n 2 ] f ( σ , σ n ) , f ( σ , σ n ) = C \begin{aligned}p(x|D)&=\int p(x|\mu)p(\mu|D)d\mu\\ &=\frac{1}{2\pi \sigma\sigma_n}exp\left[-\frac{1}{2}\frac{(x-\mu_n)^2}{\sigma^2+\sigma_n^2}\right]f(\sigma,\sigma_n),\;f(\sigma,\sigma_n)=C \end{aligned} p(x∣D)=∫p(x∣μ)p(μ∣D)dμ=2πσσn1exp[−21σ2+σn2(x−μn)2]f(σ,σn),f(σ,σn)=C即 p ( x ∣ D ) ∼ N ( μ n , σ 2 + σ n 2 ) p(x|D)\sim N(\mu_n,\sigma^2+\sigma_n^2) p(x∣D)∼N(μn,σ2+σn2),如果是最大似然估计,则 p ( x ∣ D ) ∼ N ( μ ^ n , σ 2 ) p(x|D)\sim N(\hat \mu_n,\sigma^2) p(x∣D)∼N(μ^n,σ2)
递归贝叶斯学习: 增加一个样本时参数分布更新一次
p ( θ ∣ D n ) = p ( D n , θ ) ∫ p ( D n , θ ) d θ = p ( x n ∣ θ ) p ( D n − 1 , θ ) ∫ p ( x n ∣ θ ) p ( D n − 1 , θ ) d θ = p ( x n ∣ θ ) p ( θ ∣ D n − 1 ) p ( D n − 1 ) ∫ p ( x n ∣ θ ) p ( θ ∣ D n − 1 ) p ( D n − 1 ) d θ = p ( x n ∣ θ ) p ( θ ∣ D n − 1 ) ∫ p ( x n ∣ θ ) p ( θ ∣ D n − 1 ) d θ p ( θ ∣ D 0 ) = p ( θ ) ∝ p ( x n ∣ θ ) p ( θ ∣ D n − 1 ) \begin{aligned} p(\theta|D^n)&=\frac{p(D^n,\theta)}{\int p(D^n,\theta)d\theta}\\ &=\frac{p(x_n|\theta)p(D^{n-1},\theta)}{\int p(x_n|\theta)p(D^{n-1},\theta)d\theta}\\ &=\frac{p(x_n|\theta)p(\theta|D^{n-1})p(D^{n-1})}{\int p(x_n|\theta)p(\theta|D^{n-1})p(D^{n-1})d\theta}\\ &=\frac{p(x_n|\theta)p(\theta|D^{n-1})}{\int p(x_n|\theta)p(\theta|D^{n-1})d\theta}\qquad p(\theta|D^0)=p(\theta)\\ &\propto p(x_n|\theta)p(\theta|D^{n-1}) \end{aligned} p(θ∣Dn)=∫p(Dn,θ)dθp(Dn,θ)=∫p(xn∣θ)p(Dn−1,θ)dθp(xn∣θ)p(Dn−1,θ)=∫p(xn∣θ)p(θ∣Dn−1)p(Dn−1)dθp(xn∣θ)p(θ∣Dn−1)p(Dn−1)=∫p(xn∣θ)p(θ∣Dn−1)dθp(xn∣θ)p(θ∣Dn−1)p(θ∣D0)=p(θ)∝p(xn∣θ)p(θ∣Dn−1)
3、半参数方法
特征维数问题: 增加特征维数优点:可以使得 样本差异增大,区分性更好;缺点:计算、存储复杂性高、模型泛化性能差。根据二类高斯分布可以得出结论:特征维度越大、均值差越大、方差越小,则错误率越小。
但特征维度越高,需要更多的样本来减小误差。
克服过拟合的方法:
1)特征降维:特征变换、特征选择
2)参数共享/平滑:共享协方差矩阵、收缩。
3.1期望最大化算法(EM)
样本中有隐藏变量或缺失样本,如果高斯混合模型中的权值 π \pi π和参数 μ , Σ \mu,\Sigma μ,Σ等。
E-step:根据已知参数对隐藏变量求期望。
M-step:最大化期望,求得参数的更新值。
1、选择一个初始值 Θ 0 \Theta ^0 Θ0
2、Do
\qquad E-step:求 p ( Z ∣ X , Θ o l d ) p(Z|X,\Theta ^{old}) p(Z∣X,Θold),计算 Q ( Θ , Θ o l d ) = ∑ Z [ l o g p ( X , Z ∣ Θ ) ] p ( Z ∣ X , Θ o l d ) Q(\Theta,\Theta^{old})=\sum_{Z}[log\;p(X,Z|\Theta)]p(Z|X,\Theta^{old}) Q(Θ,Θold)=∑Z[logp(X,Z∣Θ)]p(Z∣X,Θold)
\qquad M-step:更新参数 Θ n e w = a r g m a x Θ Q ( Θ , Θ o l d ) \Theta^{new}=\underset{\Theta}{argmax} Q(\Theta,\Theta^{old}) Θnew=ΘargmaxQ(Θ,Θold)
\qquad 判断条件终止
3、End
3.2隐马尔可夫模型(HMM)
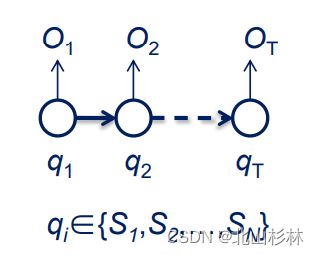
观察序列: O = O 1 O 2 . . . O T \textbf{O}=O_1O_2...O_T O=O1O2...OT, O t ∈ { v 1 , . . . v M } O_t\in \{v_1,...v_M\} Ot∈{v1,...vM},v为观测值。
状态序列: q = q 1 q 2 . . . q T \textbf{q}=q_1q_2...q_T q=q1q2...qT, q t ∈ { S 1 , . . . S N } q_t\in \{S_1,...S_N\} qt∈{S1,...SN},S为状态。
目标: P ( q ∣ O ) P(\textbf{q}|\textbf{O}) P(q∣O)
对于一阶马尔可夫链,有 P ( q 1 q 2 . . . q T ) = P ( q 1 ) P ( q 2 ∣ q 1 ) . . . P ( q T ∣ q T − 1 ) P(q_1q_2...q_T)=P(q_1)P(q_2|q_1)...P(q_T|q_{T-1}) P(q1q2...qT)=P(q1)P(q2∣q1)...P(qT∣qT−1)
转移概率: a i j = P ( q t = S i ∣ q t + 1 = S j ) a_{ij}=P(q_t=S_i|q_{t+1}=S_j) aij=P(qt=Si∣qt+1=Sj)
释放概率: b j ( k ) = P ( O t = v k ∣ q t = S j ) b_j(k)=P(O_t=v_k|q_t=S_j) bj(k)=P(Ot=vk∣qt=Sj),表示在t时刻状态为 S j S_j Sj的条件下,观察值为 v k v_k vk的概率。
初始分布: π = { π i } \pi=\{ \pi_i \} π={πi}, π i = P ( q 1 = S i ) \pi_i=P(q_1=S_i) πi=P(q1=Si)
模型参数集合: λ = ( A , B , π ) \lambda=(A,B,\pi) λ=(A,B,π),分别为转移概率矩阵、释放概率矩阵、初始分布。
一、评估
P ( O ∣ λ ) = ∑ a l l Q P ( O ∣ Q , λ ) P ( Q ∣ λ ) = ∑ q 1 , q 2 . . . q T π q 1 b q 1 ( O 1 ) a q 1 q 2 b q 2 ( O 2 ) . . . a q T − 1 q T b q T ( O T ) \begin{aligned} P(O|\lambda)&=\sum_{all\;Q}P(O|Q,\lambda)P(Q|\lambda)\\ &=\sum_{q_1,q_2...q_T}\pi_{q_1}b_{q_1}(O_1)a_{q_1q_2}b_{q_2}(O_2)...a_{q_{T-1}q_T}b_{q_T}(O_T) \end{aligned} P(O∣λ)=allQ∑P(O∣Q,λ)P(Q∣λ)=q1,q2...qT∑πq1bq1(O1)aq1q2bq2(O2)...aqT−1qTbqT(OT)算法复杂度太高,此时可以利用前向算法或后向算法:
二、解码
维特比算法:
三、训练
BW算法:
4、非参数方法
非参数方法主要是概率密度函数的形式未知。
局部特征空间中一定样本的比率: P = ∫ R p ( x ′ ) d x ′ ≃ p ( x ) V \rm P=\int_R p(x')dx'\simeq p(x)V P=∫Rp(x′)dx′≃p(x)V, p ( x ) = ≃ k / n V \rm p(x)=\simeq\frac{k/n}{V} p(x)=≃Vk/n,其中n为样本总数,V为区域体积,k为区域内样本个数。 P P P为概率, p ( x ) \rm p(x) p(x)为概率密度。
非参数密度估计方法:
1)parzen window:固定区域体积V,k变换。
2)k-nearest neighbor:固定局部样本数k,V变化。
4.1帕森窗
以x为中心,体积为 V n V_n Vn的局部区域内样本数为:( x i x_i xi是否在以x为中心的窗函数内)
k n = ∑ i = 1 n φ ( x − x i h n ) k_n=\sum_{i=1}^n\varphi \left(\frac{x-x_i}{h_n}\right) kn=i=1∑nφ(hnx−xi)概率密度估计
p n ( x ) = 1 n V n ∑ i = 1 n φ ( x − x i h n ) p_n(x)=\frac{1}{nV_n}\sum_{i=1}^n\varphi \left(\frac{x-x_i}{h_n}\right) pn(x)=nVn1i=1∑nφ(hnx−xi)其中窗函数需要满足要求 φ ( x ) ≥ 0 , ∫ φ ( u ) d u = 1 \varphi(x)\ge 0,\quad\int\varphi(u)du=1 φ(x)≥0,∫φ(u)du=1; h n h_n hn决定窗口的宽度。

当窗口宽度过小时,会导致过拟合,当窗口宽度过大时,导致欠拟合 。选取原则:(1)密度越大,窗口越小,如 V n = V 1 / n V_n=V_1/\sqrt n Vn=V1/n;(2)随x变化 h ( x ) h(x) h(x);(3)交叉验证。设置多个候选值进行交叉验证。
4.2K近邻估计
p n ( x ) p_n(x) pn(x)收敛到 p ( x ) p(x) p(x)的条件: lim n → ∞ k n = ∞ a n d lim n → ∞ k n / n = 0 \lim_{n \to \infty} k_n=\infty \;and\;\lim_{n \to \infty}k_n/n=0 limn→∞kn=∞andlimn→∞kn/n=0
一维例子:
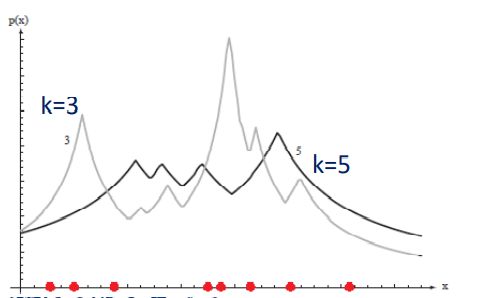
当k和n确定时,窗口越小,概率越大。
KNN分类的后验概率:
设 k = ∑ i = 1 c k i k=\sum_{i=1}^ck_i k=∑i=1cki表示所有c个类别,窗口中每个类别样本个数为 k i k_i ki。
P n ( ω i ∣ x ) = p n ( x , ω i ) ∑ i = 1 c p n ( x , ω i ) = k i k p n ( x , ω i ) = k i / n V P_n(\omega_i|x)=\frac{p_n(x,\omega_i)}{\sum_{i=1}^cp_n(x,\omega_i)}=\frac{k_i}{k}\\ p_n(x,\omega_i)=\frac{k_i/n}{V} Pn(ωi∣x)=∑i=1cpn(x,ωi)pn(x,ωi)=kkipn(x,ωi)=Vki/n当达到收敛条件时,分类错误率趋近于贝叶斯分类器。
最近邻分类器的错误率:
K近邻搜索的三种加速策略:
(1)部分距离:如做最近邻分类时,每个样本为d维,但比较时如果计算到前r维的差的平方和已经大于最小距离则不再进行计算。 D r 2 ( a , b ) = ∑ i = 1 r ( a i − b i ) 2 , ( r < d ) D_r^2(a,b)=\sum_{i=1}^r(a_i-b_i)^2,\quad(r
(2)预结构化:分层搜索的思想,比如对于最近邻分类器,可以先将训练样本进行聚类,取每个聚类中心作为代表点,每次先计算测试样本与代表点之间的距离,找到最小的距离,然后在该聚类中寻找距离最近的训练样本点。这样做有一定风险,因此在实际操作中常常找最小的k个测试样本与代表点距离。
(3)编辑:将周围全是同一类样本的训练样本点去掉,以减小计算量。
(4)branch-and-bound、k-d tree等算法。
K近邻分类器的作用:
(1)做实际分类器
(2)作为参照分类器(当训练样本比较多时,其分类性能很好,但计算量巨大)
4.3距离度量:
距离度量(metric)的性质:非负性、对称性、自反性、满足三角不等式。
Minkowski距离: L k ( a , b ) = ( ∑ i = 1 d ∣ a i = b i ∣ k ) 1 / k L_k(a,b)=\left(\sum_{i=1}^d|a_i=b_i|^k\right)^{1/k} Lk(a,b)=(∑i=1d∣ai=bi∣k)1/k
曼哈顿据距离、欧几里得距离、切比雪夫距离…
二值特征的Tanimoto metric:谷本度量。
D T a n i m o t o ( S 1 , S 2 ) = n 1 + n 2 − 2 n 12 n 1 + n 2 − n 12 D_{Tanimoto}(S_1,S_2)=\frac{n_1+n_2-2n_{12}}{n_1+n_2-n_{12}} DTanimoto(S1,S2)=n1+n2−n12n1+n2−2n12其中 n 1 n_1 n1、 n 2 n_2 n2分别为集合 S 1 S_1 S1、 S 2 S_2 S2的元素个数。 n 12 n_{12} n12是交集元素个数。
切线距离Tangent distance:
度量学习:根据不同的任务自主学习不同的距离度量。有线性变换和非线性变换两种模式。
5、线性判别函数
线性判别函数假定判别函数的参数已知,直接从样本估计判别函数的参数。
模式分类的三种途径:
(1)估计类条件概率密度函数(贝叶斯决策)。
(2)直接估计后验概率(KNN)。
(3)直接计算判别函数(支持向量机)。
5.1线性判别
二分类线性判别函数:
g ( x ) = w T x + w 0 \rm g(x)=w^Tx+w_0 g(x)=wTx+w0 g ( x ) = 0 g(x)=0 g(x)=0为决策面。

x = x p + r w ∣ ∣ w ∣ ∣ g ( x p ) = 0 g ( x ) = w T ( x p + r w ∣ ∣ w ∣ ∣ ) + w o = r ∣ ∣ w ∣ ∣ r = g ( x ) ∣ ∣ w ∣ ∣ \begin {aligned} &x=x_p+r\frac{w}{||w||}\\ &g(x_p)=0\\ &g(x)=w^T(x_p+r\frac{w}{||w||})+w_o=r||w||\\ &r=\frac{g(x)}{||w||} \end{aligned} x=xp+r∣∣w∣∣wg(xp)=0g(x)=wT(xp+r∣∣w∣∣w)+wo=r∣∣w∣∣r=∣∣w∣∣g(x)多分类:
(1)one-vs-all:c个分类器
(2)one-vs-one:从c(c+1)/2个分类器
(3)逐步一对多:类似树形结构
(4)线性机器:上述分类方法会存在不确定性区域,线性机器,对 i ≠ j i\ne j i=j,如果 g i ( x ) > g j ( x ) g_i(x)>g_j(x) gi(x)>gj(x),则分为第i类。
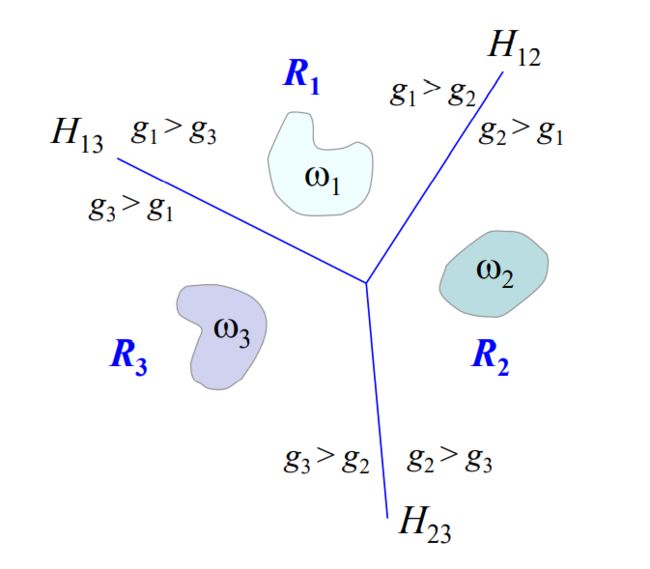
线性决策面的优点:决策区域是凸的,且决策区域是单连通的,便于分析,但不利于复杂数据的分类。
5.2广义线性判别
将样本x通过非线性映射为y,在新的数据空间可以应用线性判别函数。
g ( x ) = ∑ i = 1 d ^ a i y i ( x ) = a T y g(x)=\sum_{i=1}^{\hat d}a_iy_i(x)=\rm a_Ty g(x)=i=1∑d^aiyi(x)=aTy当新空间的维数足够高时, g ( x ) g(x) g(x)可以逼近任意线性判别函数,但会带来维数灾难。
线性判别函数齐次增广表示: g ( x ) = w T x + w o = a T y \rm g(x)=w^Tx+w_o=a^Ty g(x)=wTx+wo=aTy
5.3感知准则函数
线性可分:对于 y ∈ ω 1 y\in \omega_1 y∈ω1,均有 a T y > 0 a^Ty>0 aTy>0;对于 y ∈ ω 2 y\in \omega_2 y∈ω2,均有 a T y < 0 a^Ty<0 aTy<0。
样本规范化:将属于 ω 2 \omega_2 ω2的样本 y y y变为 − y -y −y,则得到 a T y > 0 a^Ty>0 aTy>0。
规范化增广样本:先增广齐次化再规范化。
准则函数:
J p ( a ) = ∑ y ∈ Y ( − a T y ) J_p(a)=\sum_{y\in Y}(-a^Ty) Jp(a)=y∈Y∑(−aTy)其中 Y Y Y为错分样本集合。 J p ( a ) J_p(a) Jp(a)总是大于零。因此优化目标是: m i n a J p ( a ) \underset{a}{min} \;J_p(a) aminJp(a)
∂ J p ( a ) ∂ a = − ∑ y ∈ Y y a k + 1 = a k + η ∑ y ∈ Y y \begin{aligned} \frac{\partial J_p(a)}{\partial a} =-\sum_{y\in Y}y\\ a_{k+1}=a_k+\eta \sum_{y\in Y}y \end{aligned} ∂a∂Jp(a)=−y∈Y∑yak+1=ak+ηy∈Y∑y 其他学习准则:
线性准则:
J p ( a ) = ∑ y ∈ Y ( − a T y ) J_p(a)=\sum_{y\in Y}(-a^Ty) Jp(a)=y∈Y∑(−aTy)平方准则:
J q ( a ) = ∑ y ∈ Y ( a T y ) 2 J_q(a)=\sum_{y\in Y}(a^Ty)^2 Jq(a)=y∈Y∑(aTy)2松弛准则:
J r ( a ) = 1 2 ∑ y ∈ Y ( a T y − b ) 2 ∣ ∣ y ∣ ∣ 2 J_r(a)=\frac{1}{2}\sum_{y\in Y}\frac{(a^Ty-b)^2}{||y||^2} Jr(a)=21y∈Y∑∣∣y∣∣2(aTy−b)2其中 Y Y Y为 a T y < b a^TyaTy<b的集合。线性准则是分段线性。故梯度不连续;平方准则过于光滑,收敛速度慢,且易受到长样本的影响。松弛方法的训练过程为:
∂ J p ( a ) ∂ a = ∑ y ∈ Y a T y − b ∣ ∣ y ∣ ∣ y a k + 1 = a k − η k ∑ y ∈ Y a T y − b ∣ ∣ y ∣ ∣ y \begin{aligned} \frac{\partial J_p(a)}{\partial a} =\sum_{y\in Y}\frac{a^Ty-b}{||y||}y\\ a_{k+1}=a_k-\eta_k \sum_{y\in Y}\frac{a^Ty-b}{||y||}y \end{aligned} ∂a∂Jp(a)=y∈Y∑∣∣y∣∣aTy−byak+1=ak−ηky∈Y∑∣∣y∣∣aTy−by
5.4最小均方误差(MSE)准则函数
将 a T y i > 0 a^Ty_i>0 aTyi>0改写为 a T y i = b i > 0 a^Ty_i=b_i>0 aTyi=bi>0,由此可以得到一个线性方程组: Y a = b \rm Ya=b Ya=b,若 Y \rm Y Y可逆,则 a = Y − 1 b \rm a=Y^{-1}b a=Y−1b,但通常情况 Y Y Y不是方阵,即样本维度与样本个数不相等,因此我们定义误差向量 e = Y a − b \rm e=Ya-b e=Ya−b,则得到平方误差准则函数:
J s ( a ) = ∣ ∣ e ∣ ∣ 2 = ∣ ∣ Y a − b ∣ ∣ 2 = ∑ i = 1 n ( a T y i − b i ) 2 J_s(a)=||e||^2=||Ya-b||^2=\sum_{i=1}^n(a^Ty_i-b_i)^2 Js(a)=∣∣e∣∣2=∣∣Ya−b∣∣2=i=1∑n(aTyi−bi)2训练过程:
∂ J s ( a ) ∂ a = 2 Y T ( Y a − b ) = 0 \frac{\partial J_s(a)}{\partial a}=2Y^T(Ya-b) =0 ∂a∂Js(a)=2YT(Ya−b)=0 a = ( Y T Y ) − 1 Y T b = Y + b a=(Y^TY)^{-1}Y^Tb=Y^+b a=(YTY)−1YTb=Y+b
可以通过上式直接求解,在应用中防止矩阵不可逆加入正则化技术: Y + ≈ ( Y T Y + ε I ) − 1 Y T Y^+\approx (Y^TY+\varepsilon I)^{-1}Y^T Y+≈(YTY+εI)−1YT。或者通过梯度下降的方法求解。
Widrow_Hoff方法:即序列最小平方更新方法 a k + 1 = a k + η ( b k − ( a k ) T y k ) y k a_{k+1}=a_k+\eta(b_k-(a_k)^Ty^k)y^k ak+1=ak+η(bk−(ak)Tyk)yk,只考虑单个样本对误差的贡献。通常情况下迭代会无穷次进行,因为W-H方法寻求更正不相等的情况 ( a k ) T y k ≠ b k (a_k)^Ty^k\ne b_k (ak)Tyk=bk,在实际中几乎不可逆,因此在训练过程中通常会让学习率随迭代次数减小。

如上图,MSE准则函数找到的超平面会有这样的问题,即黑线和红线的样本到超平面的距离平方和相同,从而找到一个错误解。
Ho-Kashyap方法:假设训练样本线性可分,对于所有样本有 a T y i > 0 a^Ty_i>0 aTyi>0,即一定存在一个a和b使得 Y a = b > 0 Ya=b>0 Ya=b>0。但是事先并不知道b,因此将MSE准则函数变为:
J s ( a , b ) = ∣ ∣ Y a − b ∣ ∣ 2 , b > 0 J_s(a,b)=||Ya-b||^2,\;b>0 Js(a,b)=∣∣Ya−b∣∣2,b>0求梯度得:
∂ J s ( a , b ) ∂ a = 2 Y T ( Y a − b ) , ∂ J s ( a , b ) ∂ b = − 2 ( Y a − b ) \frac{\partial J_s(a,b)}{\partial a} =2Y^T(Ya-b),\;\frac{\partial J_s(a,b)}{\partial b} =-2(Ya-b) ∂a∂Js(a,b)=2YT(Ya−b),∂b∂Js(a,b)=−2(Ya−b)由于b需要满足约束条件 b > 0 b>0 b>0,故b得更新公式可以为:
b k + 1 = b k − η k 1 2 ( ∂ J s ( a , b ) ∂ b − ∣ ∂ J s ( a , b ) ∂ b ∣ ) = b k + 2 η k e k + a k = Y + b k \begin{aligned}b_{k+1}&=b_k-\eta_k\frac{1}{2}\left (\frac{\partial J_s(a,b)}{\partial b} -\left | \frac{\partial J_s(a,b)}{\partial b} \right | \right) =b_k+2\eta_ke_k^+\\ a_k&=Y^+b_k \end{aligned} bk+1ak=bk−ηk21(∂b∂Js(a,b)− ∂b∂Js(a,b) )=bk+2ηkek+=Y+bk为了防止b收敛到0,初始化的时候需要让b从一个非负向量开始。
5.5多类线性判别函数
(1)MSE多类扩展: y = W T x + b \rm y=W^Tx+b y=WTx+b,此时不用规范化增广坐标,决策规则为:如果 j = a r g m a x ( W T x + b ) j=arg\;max(W^Tx+b) j=argmax(WTx+b),则 x ∈ ω j x\in \omega_j x∈ωj。 Y Y Y是用one-hot向量组成的矩阵。优化目标为:
m i n W , b ∑ i = 1 n ∥ W T x − b − y i ∥ 2 2 = m i n W ^ ∥ W ^ T X ^ − y ∥ 2 2 \underset{W,b}{min} \sum_{i=1}^{n} \left \| W^Tx-b-y_i \right \|_2^2=\underset{\hat W}{min} \left \| \hat W^T\hat X-y \right \|_2^2 W,bmini=1∑n WTx−b−yi 22=W^min W^TX^−y 22其中:
W ^ = ( W b T ) , x ^ = ( x 1 ) \hat W=\begin{pmatrix} W\\ b^T \end{pmatrix},\quad \hat x=\begin{pmatrix} x \\ 1 \end{pmatrix} W^=(WbT),x^=(x1)解得: W ^ = ( X ^ X T ^ ) − 1 X ^ Y T \hat{W}=(\hat{X}\hat{X^T})^{-1}\hat{X}Y^T W^=(X^XT^)−1X^YT。
(2)感知器准则扩展方法
(3)Kelser构造。
6、人工神经网络
6.1简要介绍
1956年,明斯基、西蒙、麦卡锡等人 首次提出人工智能的概念。
人工神经网络的三次浪潮:
1、1960s:感知机、自适应线性单元
2、1980s:Hopfield网络、Boltzman机、BP算法
3、2000s:深度网络、Deep-CNN、RNN
激活函数: 作用是将可能的无限域变换到指定的有限范围内输出。
要求:非线性、连续可到、单调(否则会产生很多局部极小值点)
软饱和函数:指x趋于无穷时导数为0,如sigmod函数。梯度消失,导致难以训练深层网络。
硬饱和函数:x超过某一阈值时,导数为零,如ReLU函数。会导致网络稀疏性和部分神经元死亡(输出为0),其次ReLU会使得输出具有偏移现象(即输均值恒大于0),会影响到神经网络的收敛性。
深度与宽度问题:
1、隐藏层个数(深度):决定网络的表达能力,深度太深会导致过拟合
2、各层结点数(宽度):结点数太少难以建立复杂分界面,太多则泛化性能较差
神经网络训练的方法:
1、Hebb训练方法:
w i j ( t + 1 ) = w i j t + η y i z j w_{ij}^{(t+1)}=w_{ij}^{t} +\eta y_iz_j wij(t+1)=wijt+ηyizj如果两个相互连接的神经元输出具有相同的符号,则增加他们之间的权重(但需要设置阈值,防止无约束增长)
2、 δ \delta δ训练方法(分析方法):按照差值最小(处理单元所要求的输出与当前实际输出间的差值)准则连续修正连接权重的强度。训练策略为梯度下降法:
Δ w i j = − η ∂ E ∂ w i j \Delta w_{ij}=-\eta \frac{\partial E}{\partial w_{ij}} Δwij=−η∂wij∂E其中 E E E时与训练样本相关的能量。
3、随机训练方法:随机改变一个权重,计算改变后网络的能量,若能量降低则接受改变。模拟退火算法就是一种随机训练算法。
4、Kohonen训练方法:在训练过程中结点参与竞争,具有最大输出的结点获胜,获胜的结点可以抑制其竞争者并激活其邻近结点,即只有获胜者和其邻近结点的权重才可以调节。
6.2前馈神经网络(感知机)
δ \delta δ规则、反向传播。权重的梯度等于连接边起点的输出乘以经终点导数放缩后的误差 Δ w i j = x i f ′ ( n e t j ) ( t j − y j ) \Delta w_{ij}=x_if'(net_j)(t_j-y_j) Δwij=xif′(netj)(tj−yj)。
防止过拟合的技术:
1、权重2范数正则化
2、权重启发式目标函数修正策略
附加冲量项: 尽快逃离饱和区。
w ( t + 1 ) = w ( t ) + ( 1 − α ) Δ b p w ( t ) + α [ w ( t ) − w ( t − 1 ) ] \rm w(t+1)=w(t)+(1-\alpha)\Delta _{bp}w(t)+\alpha [w(t)-w(t-1)] w(t+1)=w(t)+(1−α)Δbpw(t)+α[w(t)−w(t−1)]
BP算法存在的问题:
1、网络麻痹现象:权重修正时,误差 δ \delta δ正比于 f ′ ( n e t ) f'(net) f′(net),当 f ′ ( n e t ) f'(net) f′(net)趋于0时,训练过程便停顿下来。可以优化目标准则函数。
2、梯度消失:多层神经网络,越靠近输入层越容易出现此问题。
3、局部极小:误差曲面非凸,可以引入随机因素。
6.3径向基函数网络
径向基函数(Radial Basis Function)是一类取值仅依赖于距离的函数。如高斯函数 ϕ k ( x ) = e x p ( − ∥ x − x k ∥ 2 σ 2 ) \phi _k(x)=exp\left ( -\frac{\left \| x-x_k \right \| }{2\sigma ^2} \right ) ϕk(x)=exp(−2σ2∥x−xk∥)。
径向基函数神经网络:
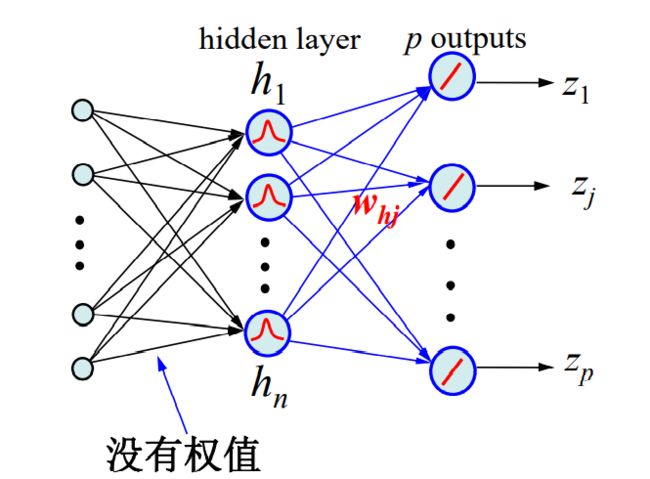
三层网络可以拟合任意函数,径向基函数网络也是三层结构,输入层到隐藏层权重为1,训练时主要改变隐藏层到输出层的权重,隐藏层的激活函数为高斯径向基函数,输出层的激活函数可以为线性函数也可以为其他函数。其隐藏层结点数等于样本个数,结构简化:对于大规模数据,首先做聚类,使隐藏层节点个数等于聚类中心个数,简化网络模型的同时增加网络的泛化能力。
6.4Hopfield网络
Hopfield网络按照动力学方式进行,其工作过程为状态的演化过程,即从初始状态按照能量减小的方向进行演化,直到达到稳定状态。具体介绍见Hopfield神经网络。其有两个主要作用:充当存储器、求解TSP问题。
6.5玻尔兹曼机(BM)
玻尔兹曼机是一种随机的Hopfield网络,是具有隐藏单元的反馈网络。
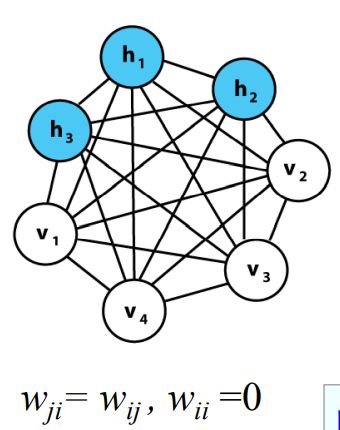
如图,玻尔兹曼机的一部分神经元是可观测的,起到输出输入作用,另一部分不可观测是隐藏结点。
受限玻尔兹曼机(RBM):
两层结构,层内结点互不相连,信息可以在层间流动,包含可视结点层和隐藏层。模型参数为 θ = { w , a , b } \theta=\{w,a,b\} θ={w,a,b},网络的能量函数为:
E ( v , h , θ ) = − ∑ i j w i j v i h j − ∑ i b i v i − ∑ j a j h j E(v,h,\theta)=-\sum_{ij}w_{ij}v_ih_j-\sum_ib_iv_i-\sum_ja_jh_j E(v,h,θ)=−ij∑wijvihj−i∑bivi−j∑ajhj可见状态与隐含状态的联合概率分布:
p θ ( v , h ) = 1 z ( θ ) e x p ( − E ( v , h , θ ) ) p_{\theta}(v,h)=\frac{1}{z(\theta)}exp(-E(v,h,\theta)) pθ(v,h)=z(θ)1exp(−E(v,h,θ))目标是对于N个样本 m a x ∑ i = 1 N l o g p ( v i ) max \sum_{i=1}^Nlog\;p(v_i) max∑i=1Nlogp(vi)。根据联合概率可以计算边缘概率和条件概率。
具体推导细节见RBM受限玻尔兹曼机,训练过程见受限玻尔兹曼机RBM最通俗易懂的教程。
6.6深度信念网络、深度玻尔兹曼机
可以将受限玻尔兹曼机等价为一个无穷层的单向网络
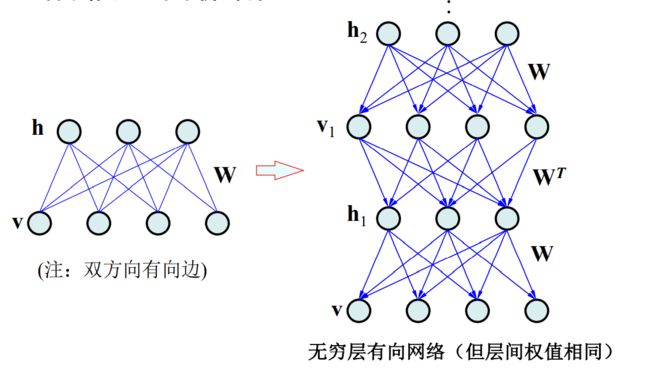
深度信念网络(DBN):其最高层为双向连接。
训练过程:对于特征学习,采用多个RBM进行贪婪训练;对于分类任务,附加一个前向网络,采用有标签的数据进行微调(fine-tuning)。
深度玻尔兹曼机(DBM):每两层之间均为双向连接。
6.7自组织映射(SOM)
主要思想:T.Kohonen认为神经网络中邻近的各个神经元通过侧向交互作用彼此竞争,自适应地发展成检测不同信号的特殊检测器。
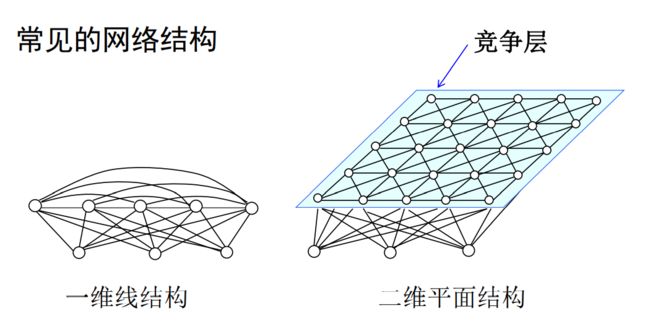
如图,神经网络的输出层各神经元结点之间相互作用。SOM获胜神经元对齐邻近神经元的影响由远及近地由兴奋转变为抑制(窗口可以变化,权重作用的邻域随时间增加而减小)。如下图函数: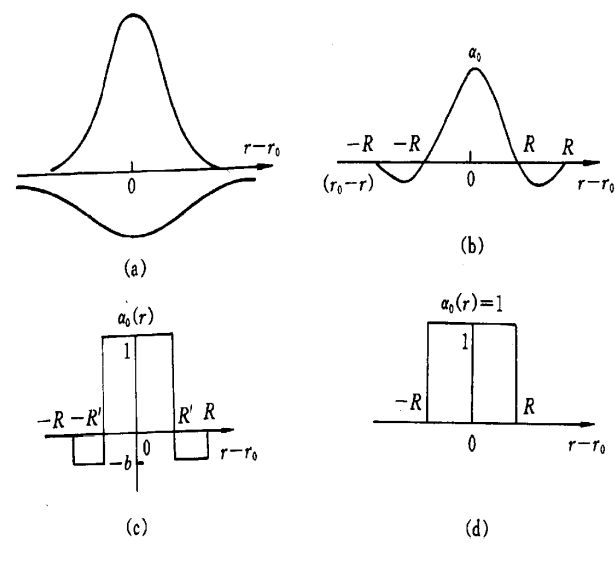
原理:自动寻找样本的内在规律和本质属性,自组织、自适应改变网络参数与结构。通过自组织特征映射算法,能够自动找出输入样本之间的相似度。
相似度准则:输入向量与映射层权重向量的欧式距离 d j = ∑ i = 1 d ( x i − w i j ) 2 d_j=\sqrt {\sum_{i=1}^d(x_i-w_{ij})^2} dj=∑i=1d(xi−wij)2,相似度大者为获胜者,然后在获胜者 j ∗ j^* j∗邻域内 h ( . , j ∗ ) h(.,j^*) h(.,j∗)调整权重值:
Δ w i j = η h ( j , j ∗ ) ( x i − w i j ) w i j ( t + 1 ) = w i j ( t ) + Δ w i j \Delta w_{ij}=\eta h(j,j^*)(x_i-w_{ij})\\ w_{ij}(t+1)=w_{ij}(t)+\Delta w_{ij} Δwij=ηh(j,j∗)(xi−wij)wij(t+1)=wij(t)+Δwij
6.8自编码器(Autoencoder)
遇到而问题:训练时没有标签,设计一种网络使得输入与输出相等,则隐藏层记录了数据的特征,自编码器是一种表示学习方法。
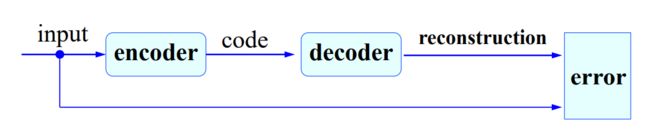
拥有多个encoder层时,采用逐层训练的方法,首先训练第一层(三层感知机),然后固定第一层,将第一层的输出作为第二层的输入训练第二层(三层感知机),以此类推。

应用:降维、降噪、缺失数据恢复。
7、特征提取
特征提取的目的:
1、减少噪声影响
2、提高稳定性
3、提取观测数据的内在特性
特征变换的目的:
1、降低空间维度,便于分析并减小计算量
2、减少特征之间可能存在的相关性
3、有利于分类
特征提取的分类:
1、根据对象:语音、文本、视觉
2、根据方式:局部特征提取(SIFT、LBP等)、全局特征提取(HoG、词袋等)
特征变换的分类:
线性变换:PCA、LDA、ICA等
非线性变换:KPCA、KLDA、Isomap、LLE、HLLE、LSTA等
7.1 语音特征提取
步骤:
1、语音信号预处理
2、分帧、加窗(低通滤波,使帧两端信号平滑过渡到0,同时帧与帧之间有重合,防止丢失信息)
3、对每一帧做数学运算得到低维向量
梅尔倒谱系数(MFCCs):
对分帧后的语音信号做傅里叶变换,丢失相位谱。
根据梅尔刻度,利用频域三角窗对傅里叶幅度谱求和。
对求和之后的值取对数
对取对数后的幅度信号做离散余弦变换得到梅尔倒谱系数特征。
7.2文本特征提取
1、向量空间模型
2、词频-逆文档频率
3、Word2Vec
7.3视觉特征提取
1、局部二值模式(LBP)
2、Gabor特征提取
3、尺度不变特征变换(SIFT)
4、视觉词袋
5、哈尔特征
6、梯度方向直方图(HoG)
8、维数缩减
8.1线性维数缩减
8.1.1 主成分分析(PCA)
8.1.2 线性判别分析(LDA)
这部分见数据降维方法(主成分分析PCA、线性判别分析LDA)。
8.2非线性维数缩减
8.2.1 多维缩放(MDS)
主要目的:将d维空间中的n个样本降维到m维空间。准则是降维之后的样本空间仍保持两两之间的距离
算法步骤:
1、给定数据,构造距离矩阵 D D D
2、构造矩阵 B B B, B = − 1 2 H T D H B=-\frac{1}{2}H^TDH B=−21HTDH
3、对矩阵 B B B进行特征值分解: B = U V T U B=UV^TU B=UVTU
4、求 Z = Λ m 1 / 2 U m T ∈ R m × n Z=\Lambda_m^{1/2}U_m^T\in R^{m\times n} Z=Λm1/2UmT∈Rm×n(选取前m个最大特征值对应的特征向量)
8.2.2流形学习
(1)LLE(局部线性嵌入): 将高维空间中样本的线性重构关系在低维空间继续保持。
在原始维度上通过周围k个样本重构样本 x i x_i xi,根据拉格朗日乘子法求出权重矩阵 W W W,利用该权重矩阵在低维空间重构新样本 y i y_i yi,并最小化重构误差。
(2)Isomap(等距特征映射): 通过K近邻等方式构造一个数据图,计算任意两点之间的测地距离,对于任意两点,期望在低维空间中保持测地距离。(经常与多维缩放一起使用,首先计算各样本之间的测地距离,然后利用MDS降维)。
(3)LE(拉普拉斯特征映射): 通过K近邻方式构造数据图,在每一个局部区域计算点与点之间的亲和度,期望点对亲和度在低维空间保持。
(4)LTSA(局部切空间对齐): 对每一个数据在局部引入一个线性变换,将其临近点映射到低维坐标系中的对应临近点。
9、特征选择
特征选择的方法:子集搜索+子集评价
9.1评价判据
直接判据:分类器的分类错误率
间接判据:不同数据的可分程度、不同类别的概率分布差异性、特征对分类的不确定性程度…
理想的评价准则应该满足:对于独立特征评价准则具有可加性;是一个度量;是特征数目的单调函数(新加入特征不应该较少可分度);与分类错误率具有正相关,反映特征的分类性能。
1、基于距离的准则
可定义类间散度矩阵和类内散度矩阵,使得类间散度矩阵尽可能大,类内散度矩阵尽可能小。
2、基于分布的评价准则(基于类条件概率密度函数)
定义两个分布的距离,此距离非负、能够衡量两个分布之间的重合程度。如KL散度,KL散度不是一个度量,因为不具有对称性。
3、基于熵的评价准则(基于后验概率密度函数)
对于所有类别,后验概率越平均,越不具有区分性,越集中于某一类则越有利于分类。可以用后验概率的信息熵作为评价标准。
9.2子集搜索
子集搜索是组合问题。
搜索策略:
1、穷举法
2、前向搜索策略(每次只加入一个新特征进行评价)
3、后向搜索策略(每次只去掉一个无关特征)
4、双向搜索策略
5、随机搜索策略
最优特征搜索方法:
1、穷举法:计算量巨大。
2、分支定界法
特征选择次优方法: (贪心算法)
1、过滤式特征选择
2、包裹式特征选择
3、嵌入式特征选择
10、模型选择
11、数据聚类
11.1 k-means聚类
循环体内执行两部操作:将样本划分到k各类中心、对类内求均值获得新的类中心。
损失函数:
l ( μ , x n , z n ) = ∑ k = 1 K z n k ∣ ∣ x n − μ k ∣ ∣ 2 l(\mu,x_n,z_n)=\sum_{k=1}^Kz_{nk}||x_n-\mu_k||^2 l(μ,xn,zn)=k=1∑Kznk∣∣xn−μk∣∣2其中是0-1损失,这是非凸函数,对初始化比较敏感,容易掉入局部最优。
第一个问题:
①k怎么选?:交叉验证、专家判断、找到损失函数随k变换最大的点。
②数据维数很高时,欧氏距离不可靠:随机投影之后进行聚类,获得多个结果之后进行集成学习。
③对噪声不鲁棒:将均值改为中值向量,中点对噪声鲁棒性高。即K-Medians算法。
②是一种硬分类方法,使得每个类别区域大小相近
③无法解决非凸数据
增量式更新方法: 竞争学习、对手惩罚竞争学习。每次选择一个样本,将距离该样本较近的聚类点拉向该样本。
mean-shift聚类:滑动窗内算均值,局部区域滑倒高密度区域(窗口半径固定)、最后将重复类中心删除即可。但对噪声不鲁棒。
DBSCAN算法: 计算某样本与周围样本点的距离,小于某个阈值则认为是该样本点的朋友,当朋友个数达到最低要求时即认为这些点时一个类,故对噪声样本比较鲁棒。
11.2 高斯混合模型
p ( x ) = ∑ k = 1 K π k N ( x ∣ μ k , Σ k ) , ∑ k = 1 K π k = 1 p(x)=\sum_{k=1}^K\pi_kN(x|\mu_k,\Sigma_k),\;\sum_{k=1}^K\pi_k=1 p(x)=k=1∑KπkN(x∣μk,Σk),k=1∑Kπk=1 总共三个参数,用EM算法求解,首先固定参数对每个样本进行分类,即求
γ k ( x ) ≡ p ( k ∣ x ) = p ( k ) p ( x ∣ k ) p ( x ) = π k N ( x ∣ μ k , Σ k ) ∑ j = 1 K π j N ( x ∣ μ j , Σ j ) \begin{aligned}\gamma _k(x)\equiv p(k|x)&=\frac{p(k)p(x|k)}{p(x)}\\ &=\frac{\pi_kN(x|\mu_k,\Sigma_k)}{\sum_{j=1}^K\pi_jN(x|\mu_j,\Sigma_j)} \end{aligned} γk(x)≡p(k∣x)=p(x)p(k)p(x∣k)=∑j=1KπjN(x∣μj,Σj)πkN(x∣μk,Σk)表示样本属于第k个高斯成分的概率。然后求似然函数对三个的导数并令导数为零,则可以解出
μ j = ∑ n = 1 N γ j ( x n ) x n ∑ n = 1 N γ j ( x n ) Σ j = ∑ n = 1 N γ j ( x n ) ( x n − μ j ) ( x n − μ j ) T ∑ n = 1 N γ j ( x n ) π j = 1 N ∑ n = 1 N γ j ( x n ) \begin{aligned} \mu_j&=\frac{\sum_{n=1}^N\gamma_j(x_n)x_n}{\sum_{n=1}^N\gamma_j(x_n)}\\ \Sigma_j&=\frac{\sum_{n=1}^N\gamma_j(x_n)(x_n-\mu_j)(x_n-\mu_j)^T}{\sum_{n=1}^N\gamma_j(x_n)}\\ \pi_j&=\frac{1}{N}\sum_{n=1}^N\gamma_j(x_n) \end{aligned} μjΣjπj=∑n=1Nγj(xn)∑n=1Nγj(xn)xn=∑n=1Nγj(xn)∑n=1Nγj(xn)(xn−μj)(xn−μj)T=N1n=1∑Nγj(xn)如此按照这两步进行迭代优化。
一些问题:同样在高斯混合模型中需要面临K值得选择问题,可以借鉴k-means算法。另外防止协方差矩阵奇异,需要对其进行约束,如单位阵(欧氏距离)、对角阵(加权欧氏距离)、共享协方差矩阵等
11.3 分级聚类
是一种启发式算法,没有目标函数。由凝聚式层次聚类(自底向上)和分列式层次聚类(自顶向下)两种方式。
11.4 谱聚类(K-means in spectrum space)
广义上讲,在学习过程中应用到