传感器的一般特性
传感器的输入信号
慢变(稳态)信号:不随时间变化或变化较为缓慢(准静态)的信号
快变信号:随时间变化较快的信号(如周期或顺便信号)
一.传感器静态特性
当输入量(X)为静态(常量)或变化缓慢的信号时(如体温),讨论传感器的静态特性,输入输出关系称静态特性
静态特性可以用函数式表示为
Y = f ( x ) Y=f(x) Y=f(x)
传感器的输出输入关系或多或少地存在非线性。在不考虑迟滞
、蠕变、不稳定性等因素的情况下,其静态特性可用下列多项式
代数方程表示:
Y = a 0 + a 1 X + a 2 X + . . . a n X Y={a}_{0}+{a}_{1}X+{a}_{2}X+...{a}_{n}X Y=a0+a1X+a2X+...anX
静态特性指标
(1)线性度
(2)灵敏度
(3)精确度(精度)
(4)最小检测量和分辨力
(5)迟滞
(6)重复性
(7)稳定性
(8)漂移
1.线性度(Linearit)
在规定的条件下,传感器静态校准曲线(实际曲线)与拟合直线间最大偏差与满量程输出值的百分比称为线性度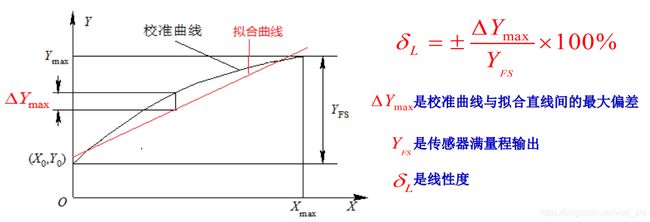
线性度与拟合的理想直线有关
理想直线的选择原则是:既能反映实际曲线的趋势,又能使非线性误差的绝对值最小。另外,还应考虑使用是否方便,计算是否简便。
常用拟合方法:
①端点连线(端基法)拟合;
②最小二乘拟合;
③理论拟合;
④端点连线平移拟合;
⑤过零旋转拟合;
实际中,常配合差动测量法来改善线性度。
差动测量方法:
利用两个性能相同的传感器进行差动输出测量。即一个传感器感受正方向变化,一个感受负方向的变化,差动输出。
设某传感器静态特性为 Y = a 0 + a 1 X + a 2 X + . . . a n X Y={a}_{0}+{a}_{1}X+{a}_{2}X+...{a}_{n}X Y=a0+a1X+a2X+...anX
则正方向传感器: Y = a 0 + a 1 X + a 2 X + a 3 X . . . Y={a}_{0}+{a}_{1}X+{a}_{2}X+{a}_{3}X... Y=a0+a1X+a2X+a3X...
负方向传感器: Y = a 0 − a 1 X + a 2 X − a 3 X . . . Y={a}_{0}-{a}_{1}X+{a}_{2}X-{a}_{3}X... Y=a0−a1X+a2X−a3X...
那么差动输出为: Δ y = a 0 − a 1 X + a 2 X − a 3 X . . . \Delta{y}={a}_{0}-{a}_{1}X+{a}_{2}X-{a}_{3}X... Δy=a0−a1X+a2X−a3X...
其优点:
①消除偶阶次非线性误差;
②灵敏度提高一倍;
③消除了零位输出
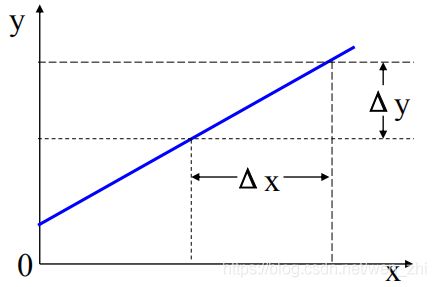
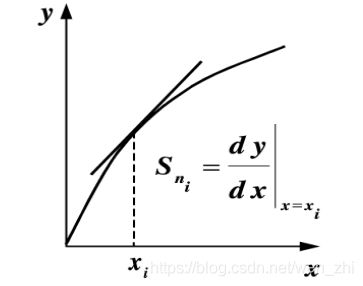
2.灵敏度(Sensitivity)
传感器的灵敏度是指到达稳定工作状态时,输出变化量与引起此变化的输入变化量之比
K = 输 出 变 化 量 输 入 变 化 量 = d y d x = d f ( x ) d x = f ′ ( x ) K= \frac{输出变化量}{输入变化量}=\frac{dy}{dx}=\frac{df(x)}{dx}={f}'(x) K=输入变化量输出变化量=dxdy=dxdf(x)=f′(x)
3.精确度
精密度:说明测量传感器输出值的分散性。精密度是随机误差大小的标志。
准确度:说明传感器输出值与真值的偏离程度。准确度是系统误差大小的标志
精确度:是精密度与准确度两者的综合优良程度。
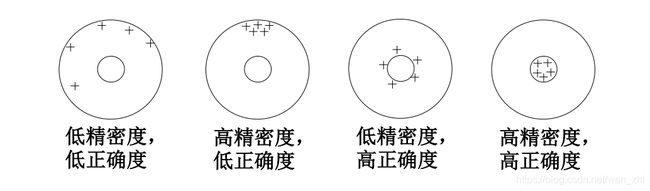

数值越小精确度越高
满量程=最大量程-最小量程
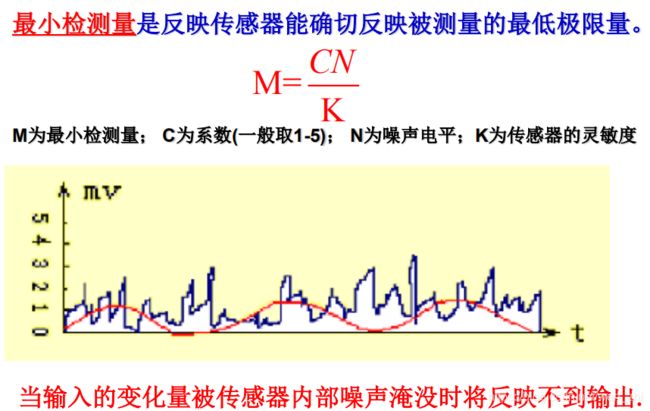
4.分辨力和最小检测量
分辨力是指传感器能检测到的最小的输入增量。有些传感器,当输入量连续变化时,输出量只作阶梯变化,则分辨力就是输出量的每个“阶梯”所代表的输入量的大小
分辨力用绝对值表示,用与满量程的百分数表示时称为分辨率。
5.迟滞
传感器在输入量由小到大(正行程)及输入量由大到小(反行程)变化期间其输入输出特性曲线不重合的现象称迟滞

6.重复性
重复性指的是传感器输入量按同一方向在全测量范围内作多次测量时,输出特性不一致的程度。重复性指标可用标准偏差来计算
7.稳定性(Stability)
稳定性表示传感器在较长时间内保持其性能参数的能力,故又称长期稳定性。
稳定性可用相对误差或绝对误差表示。表示方式如:_ 个月不超
过 %满量程输出。有时也采用给出标定的有效期来表示。
相 对 误 差 = 偏 差 大 小 满 量 程 相对误差= \frac{偏差大小}{满量程} 相对误差=满量程偏差大小
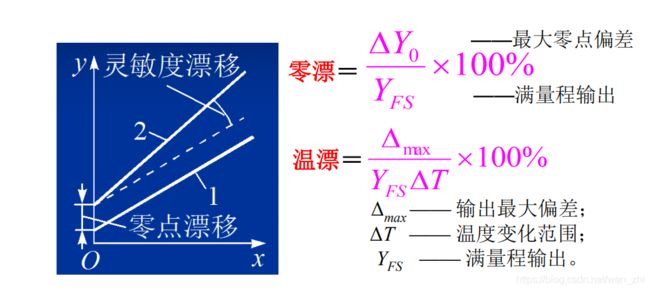
8.漂移
传感器在输入量不变的情况下,输出量随时间变化的现象。
产生原因:
- 传感器自身结构参数老化
- 测试过程中环境发生
漂移包括零点漂移和灵敏度漂移 。零点漂移和灵敏
度漂移又可分为时间漂移和温度漂移:
二.传感器动态特性
1.基本概念
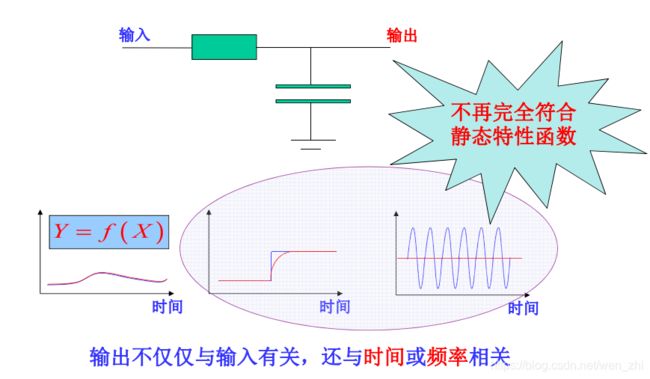
动态特性是指传感器输出对时间变化的输入量的响应特性:
除理想状态,多数传感器的输入信号是随时间变化的,输出信号一定不会与输入信号有相同的时间函数,这种输入输出之间的差异就是动态误差;(可能出现增益或者相位变化)
为什么会有动态特性?
传感器具有惯性和滞后,当被测量随时间变化时,输出量还来不及达到平衡 ,比如,温度测量,温度传感器必须达到热平衡才能测量
传感器输出对时间变化的输入量的响应即反映了传感器的动态特性。被测量是时间的函数,或是频率的函数
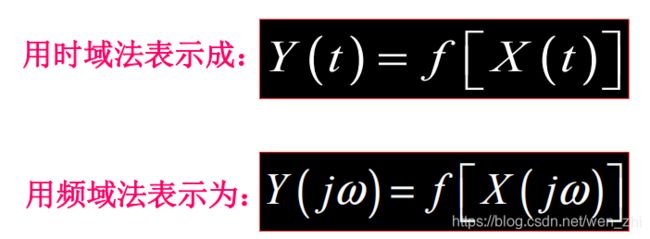
2.一般数学模型
线性系统的数学模型为一常系数线性微分方程。对线性系统动态特性的研究,主要是分析数学模型的输入量x与输出量y之间的关系,通过对微分方程求解,得出动态性能指标
对于线性定常(时间不变)系统,其数学模型为高阶常系数线性微分方程


- 零阶输入系统的输入量无论随时间如何变化,其输出量总是与输入量成确定的比例关系。
- 在时间上也不滞后,幅角等于零。如电位器式传感器。
- 在实际应用中,许多高阶系统在变化缓慢、频率不高时,都可以近似地当作零阶系统处理


3.传递函数
- 传递函数与输入信号无关,只取决系统的结构参数,换句话说它描述,是传感器自身的内部特性.
- 根据传递函数可以分析系统的频率特性
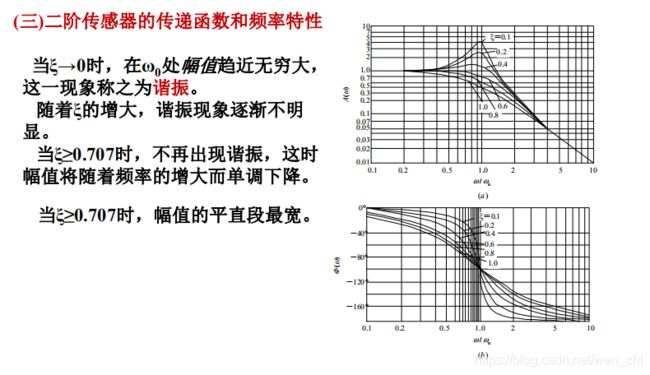
二阶传感器的频率响应特性好坏主要取决于传感器的固有频率ω0和阻尼比ξ。
4.动态响应及动态特性指标
动态特性除了与传感器的固有因素有关之外,还与传感器输入量的变化形式有关。也就是说,我们在研究传感器动特性时, 通常是根据不同输入变化规律来考察传感器的响应的
- 频域响应特性——输入为正弦信号
- 瞬态响应特性——用得较多的标准输入信号有阶跃信号和脉冲信号。
- 单位阶跃输入 f ( n ) = { X = 0 , t<0 X = 1 , t>=0 f(n) = \begin{cases} X=0, & \text{t<0} \\ X=1, & \text{t>=0} \end{cases} f(n)={X=0,X=1,t<0t>=0
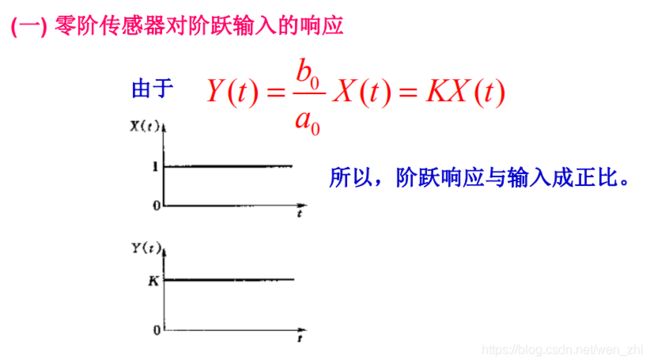

理论上传感器的响应只在t趋于无穷大时才达到稳态值,但通常认为t=(3~4)τ时,如当t=4τ时其输出就可达到稳态值的98.2%,可以认为已达到稳态。
所以, 一阶传感器的时间常数τ越小,响应越快,响应曲线越接近于输入阶跃曲线,即动态误差小。因此,τ值是一阶传感器重要的性能参数。
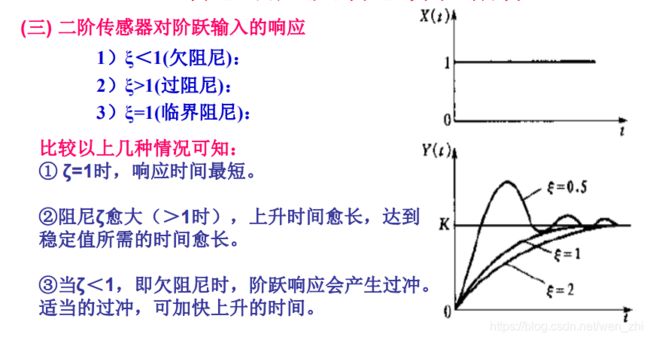
实际中,为了兼顾短的上升时间和小的过冲量,通常取ζ=0.7