Adaboost
基本原理
Adaboost采用迭代的思想,每次迭代只训练一个弱分类器,训练好的弱分类器将参与下一次迭代的使用。也就是说,在第N次迭代中,一共就有N个弱分类器,其中N-1个是以前训练好的,其各种参数都不再改变,本次训练第N个分类器。其中弱分类器的关系是第N个弱分类器更可能分对前N-1个弱分类器没分对的数据,最终分类输出要看这N个分类器的综合效果。
弱分类器(单层决策树)
Adaboost一般使用单层决策树作为其弱分类器,且其输出只有二值(1,-1)。单层决策树是决策树的最简化版本,只有一个决策点,也就是说,如果训练数据有多维特征,单层决策树也只能选择其中一维特征来做决策,并且还有一个关键点,决策的阈值也需要考虑。
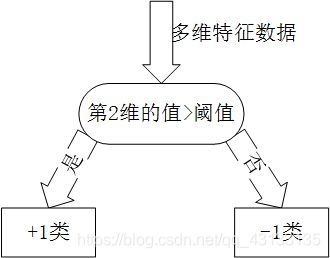
关于单层决策树的决策点,来看几个例子。比如特征只有一个维度时,可以以小于7的分为一类,标记为+1,大于(等于)7的分为另一类,标记为-1。当然也可以以13作为决策点,决策方向是大于13的分为+1类,小于(等于)13的分为-1类。在单层决策树中,一共只有一个决策点,所以下图的两个决策点不能同时选取。

同样的道理,当特征有两个维度时,可以以纵坐标7作为决策点,决策方向是小于7分为+1类,大于(等于)7分类-1类。当然还可以以横坐标13作为决策点,决策方向是大于13的分为+1类,小于13的分为-1类。在单层决策树中,一共只有一个决策点,所以下图的两个决策点不能同时选取。
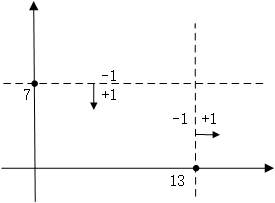
扩展到三维、四维、N维都是一样,在单层决策树中,一共只有一个决策点,所以只能在其中一个维度中选择一个合适的决策阈值作为决策点。
关于Adaboost的两种权重
Adaboost算法中有两种权重,一种是数据的权重,另一种是弱分类器的权重。其中,数据的权重主要用于弱分类器寻找其分类误差最小的决策点,找到之后用这个最小误差计算出该弱分类器的权重(发言权),分类器权重越大说明该弱分类器在最终决策时拥有更大的发言权。
Adaboost数据权重
刚刚已经介绍了单层决策树的原理,这里有一个问题,如果训练数据保持不变,那么在数据的某个特定维度上单层决策树找到的最佳决策点每一次必然都是一样的,为什么呢?因为单层决策树是把所有可能的决策点都找了一遍然后选择了最好的,如果训练数据不变,那么每次找到的最好的点当然都是同一个点了。
所以,这里Adaboost数据权重就派上用场了,所谓“数据的权重主要用于弱分类器寻找其分类误差最小的点”,其实,在单层决策树计算误差时,Adaboost要求其乘上权重,即计算带权重的误差。
举个例子,在以前没有权重时(其实是平局权重时),一共10个点时,对应每个点的权重都是0.1,分错1个,错误率就加0.1;分错3个,错误率就是0.3。现在,每个点的权重不一样了,还是10个点,权重依次是[0.01,0.01,0.01,0.01,0.01,0.01, 0.01,0.01,0.01,0.91],如果分错了第1一个点,那么错误率是0.01,如果分错了第3个点,那么错误率是0.01,要是分错了最后一个点,那么错误率就是0.91。这样,在选择决策点的时候自然是要尽量把权重大的点(本例中是最后一个点)分对才能降低误差率。由此可见,权重分布影响着单层决策树决策点的选择,权重大的点得到更多的关注,权重小的点得到更少的关注。
在Adaboost算法中,每训练完一个弱分类器都就会调整权重,上一轮训练中被误分类的点的权重会增加,在本轮训练中,由于权重影响,本轮的弱分类器将更有可能把上一轮的误分类点分对,如果还是没有分对,那么分错的点的权重将继续增加,下一个弱分类器将更加关注这个点,尽量将其分对。
这样,达到“你分不对的我来分”,下一个分类器主要关注上一个分类器没分对的点,每个分类器都各有侧重。
Adaboost分类器的权重
由于Adaboost中若干个分类器的关系是第N个分类器更可能分对第N-1个分类器没分对的数据,而不能保证以前分对的数据也能同时分对。所以在Adaboost中,每个弱分类器都有各自最关注的点,每个弱分类器都只关注整个数据集的中一部分数据,所以它们必然是共同组合在一起才能发挥出作用。所以最终投票表决时,需要根据弱分类器的权重来进行加权投票,权重大小是根据弱分类器的分类错误率计算得出的,总的规律就是弱分类器错误率越低,其权重就越高。
Adaboost分类器的训练
如图所示的Adaboost分类器的整体结构。从右到左,可见最终的求和与符号函数,再看到左边求和之前,图中的虚线表示不同轮次的迭代效果,第1次迭代时,只有第1行的结构,第2次迭代时,包括第1行与第2行的结构,每次迭代增加一行结构,图下方的“云”表示不断迭代结构的省略。

第 i i i轮迭代要做这么几件事:
- 新增弱分类器 W e a k C l a s s i f i e r i WeakClassifier_i WeakClassifieri与弱分类器权重 a l p h a i alpha_i alphai
- 通过数据集 d a t a data data与数据权重 W i W_i Wi训练弱分类器 W e a k C l a s s i f i e r i WeakClassifier_i WeakClassifieri,并得出其分类错误率,以此计算出其弱分类器权重 a l p h a i alpha_i alphai
- 通过加权投票表决的方法,让所有弱分类器进行加权投票表决的方法得到最终预测输出,计算最终分类错误率,如果最终错误率低于设定阈值(比如5%),那么迭代结束;如果最终错误率高于设定阈值,那么更新数据权重得到 W i + 1 W_{i+1} Wi+1
训练一个强分类器的流程如下
def createBosstingTree(trainDataList, trainLabelList, treeNum = 50):
'''
创建提升树
创建算法依据“8.1.2 AdaBoost算法” 算法8.1
:param trainDataList:训练数据集
:param trainLabelList: 训练数据标签集
:param treeNum: 树的层数
:return: 提升树
'''
#将数据和标签转化为数组形式
trainDataArr = np.array(trainDataList)
trainLabelArr = np.array(trainLabelList)
#预测输出结果列表
finallpredict = [0] * len(trainLabelArr)
#获得训练集数量m 以及 特征个数n
m, n = np.shape(trainDataArr)
#依据算法8.1步骤(1)初始化数据权重D为1/N ,m维数组,都是均值1 / m
D = [1 / m] * m
#初始化提升树列表,每个位置为一层
tree = []
#循环创建提升树
for i in range(treeNum):
#创建当前层的提升树
curTree = createSigleBoostingTree(trainDataArr, trainLabelArr, D)
#计算分类误差率
em=curTree['e']
#根据式8.2计算当前层的alpha
alpha = 1/2 * np.log((1 - em) / em)
curTree['alpha'] = alpha
#获得当前层的预测结果,用于下一步更新D
Gx = curTree['Gx']
#依据式8.4更新D
#考虑到该式每次只更新D中的一个w,要循环进行更新知道所有w更新结束会很复杂(其实
#不是时间上的复杂,只是让人感觉每次单独更新一个很累),所以该式以向量相乘的形式,
#一个式子将所有w全部更新完。
#该式需要线性代数基础,如果不太熟练建议补充相关知识,当然了,单独更新w也一点问题
#没有
#np.multiply(trainLabelArr, Gx):exp中的y*Gm(x),结果是一个行向量,内部为yi*Gm(xi)
#np.exp(-1 * alpha * np.multiply(trainLabelArr, Gx)):上面求出来的行向量内部全体
#成员再乘以-αm,然后取对数,和书上式子一样,只不过书上式子内是一个数,这里是一个向量
#D是一个行向量,取代了式中的wmi,然后D求和为Zm
#书中的式子最后得出来一个数w,所有数w组合形成新的D
#这里是直接得到一个向量,向量内元素是所有的w
#本质上结果是相同的
D = np.multiply(D, np.exp(-1 * alpha * np.multiply(trainLabelArr, Gx))) / sum(D)
#将当前层添加到提升树索引中。
tree.append(curTree)
#-----以下代码用来辅助,可以去掉---------------
#根据8.6式将结果加上当前层乘以α,得到目前的最终输出预测
finallpredict += alpha * Gx
#计算当前最终预测输出与实际标签之间的误差
error = sum([1 for i in range(len(trainDataList)) if np.sign(finallpredict[i]) != trainLabelArr[i]])
#计算当前最终误差率
finallError = error / len(trainDataList)
#如果误差<5%,提前退出即可,因为没有必要再计算算了
if finallError <5%: return tree
#打印一些信息
print('iter:%d:%d, sigle error:%.4f, finall error:%.4f'%(i, treeNum, curTree['e'], finallError ))
#返回整个提升树
return tree
训练一个弱分类器
def createSigleBoostingTree(trainDataArr, trainLabelArr, D):
'''
创建单层提升树
:param trainDataArr:训练数据集数组
:param trainLabelArr: 训练标签集数组
:param D: 算法8.1中的D
:return: 创建的单层提升树
'''
#获得样本数目m 及 特征数量n
m, n = np.shape(trainDataArr)
#单层树的字典,用于存放当前层提升树的参数
#也可以认为该字典代表了一层提升树
sigleBoostTree = {}
#初始化分类误差率,分类误差率在算法8.1步骤(2)(b)有提到
#误差率最高也只能100%,因此初始化为1
sigleBoostTree['e'] = 1
#对每一个特征进行遍历,寻找用于划分的最合适的特征
for i in range(n):
#因为特征已经经过二值化,只能为0和1,因此分切分时分为-0.5, 0.5, 1.5三挡进行切割
for div in [-0.5, 0.5, 1.5]:
#在单个特征内对正反例进行划分时,有两种情况:
#可能是小于某值的为1,大于某值得为-1,也可能小于某值得是-1,反之为1
#因此在寻找最佳提升树的同时对于两种情况也需要遍历运行
#LisOne:Low is one:小于某值得是1
#HisOne:High is one:大于某值得是1
for rule in ['LisOne', 'HisOne']:
#按照第i个特征,以值div进行切割,进行当前设置得到的预测G 和 分类错误率e
Gx, e = calc_e_Gx(trainDataArr, trainLabelArr, i, div, rule, D)
#如果分类错误率e小于当前最小的e,那么将它作为最小的分类错误率保存
if e < sigleBoostTree['e']:
sigleBoostTree['e'] = e
#同时也需要存储最优划分点、划分规则、预测结果、特征索引
#以便进行D更新和后续预测使用
sigleBoostTree['div'] = div
sigleBoostTree['rule'] = rule
sigleBoostTree['Gx'] = Gx
sigleBoostTree['feature'] = i
#返回单层的提升树
return sigleBoostTree
计算预测值与错误率
def predict(x, div, rule, feature):
'''
输出单独层预测结果
:param x: 预测样本
:param div: 划分点
:param rule: 划分规则
:param feature: 进行操作的特征
:return:
'''
#依据划分规则定义小于及大于划分点的标签
if rule == 'LisOne': L = 1; H = -1
else: L = -1; H = 1
#判断预测结果
if x[feature] < div: return L
else: return H
def calc_e_Gx(trainDataArr, trainLabelArr, n, div, rule, D):
'''
计算分类错误率
:param trainDataArr:训练数据集数字
:param trainLabelArr: 训练标签集数组
:param n: 要操作的特征
:param div:划分点
:param rule:正反例标签
:param D:权值分布D
:return:预测结果, 分类误差率
'''
#初始化分类误差率为0
e = 0
#将训练数据矩阵中特征为n的那一列单独剥出来做成数组。因为其他元素我们并不需要,
#直接对庞大的训练集进行操作的话会很慢
x = trainDataArr[:, n]
#同样将标签也转换成数组格式,x和y的转换只是单纯为了提高运行速度
#测试过相对直接操作而言性能提升很大
y = trainLabelArr
predict = []
#依据小于和大于的标签依据实际情况会不同,在这里直接进行设置
if rule == 'LisOne': L = 1; H = -1
else: L = -1; H = 1
#遍历所有样本的特征m
for i in range(trainDataArr.shape[0]):
if x[i] < div:
#如果小于划分点,则预测为L
#如果设置小于div为1,那么L就是1,
#如果设置小于div为-1,L就是-1
predict.append(L)
#如果预测错误,分类错误率要加上该分错的样本的权值(8.1式)
if y[i] != L: e += D[i]
elif x[i] >= div:
#与上面思想一样
predict.append(H)
if y[i] != H: e += D[i]
#返回预测结果和分类错误率e
#预测结果其实是为了后面做准备的,在算法8.1第四步式8.4中exp内部有个Gx,要用在那个地方
#以此来更新新的D
return np.array(predict), e
主流程 训练+测试
def model_test(testDataList, testLabelList, tree):
'''
测试
:param testDataList:测试数据集
:param testLabelList: 测试标签集
:param tree: 提升树
:return: 准确率
'''
#错误率计数值
errorCnt = 0
#遍历每一个测试样本
for i in range(len(testDataList)):
#预测结果值,初始为0
result = 0
#依据算法8.1式8.6
#预测式子是一个求和式,对于每一层的结果都要进行一次累加
#遍历每层的树
for curTree in tree:
#获取该层参数
div = curTree['div']
rule = curTree['rule']
feature = curTree['feature']
alpha = curTree['alpha']
#将当前层结果加入预测中
result += alpha * predict(testDataList[i], div, rule, feature)
#预测结果取sign值,如果大于0 sign为1,反之为0
if np.sign(result) != testLabelList[i]: errorCnt += 1
#返回准确率
return 1 - errorCnt / len(testDataList)
if __name__ == '__main__':
#开始时间
start = time.time()
# 获取训练集
print('start read transSet')
trainDataList, trainLabelList = loadData('../Mnist/mnist_train.csv')
# 获取测试集
print('start read testSet')
testDataList, testLabelList = loadData('../Mnist/mnist_test.csv')
#创建提升树
print('start init train')
tree = createBosstingTree(trainDataList[:10000], trainLabelList[:10000], 40)
#测试
print('start to test')
accuracy = model_test(testDataList[:1000], testLabelList[:1000], tree)
print('the accuracy is:%d' % (accuracy * 100), '%')
#结束时间
end = time.time()
print('time span:', end - start)
参考:
(机器学习)-Adaboost提升树-二分类和多分类(最清晰最易懂)
Adaboost入门教程——最通俗易懂的原理介绍(图文实例)
李航统计学习代码
