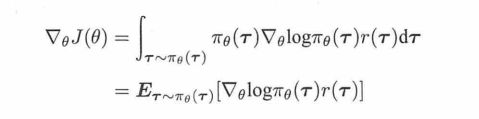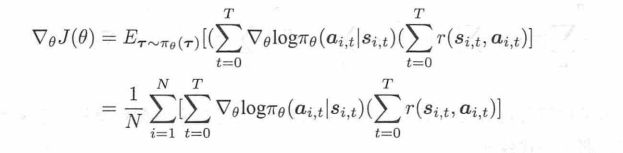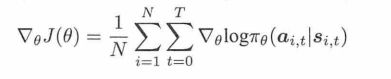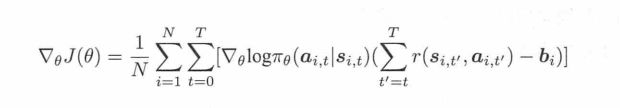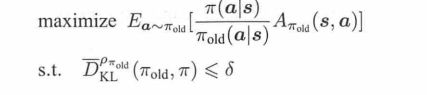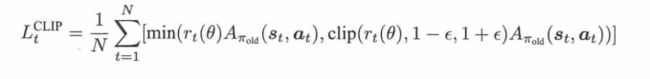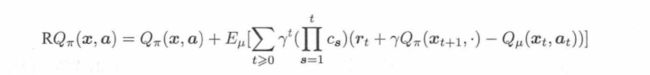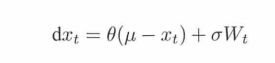深度强化学习复习摘要
离散动作空间
策略迭代:
由于环境转移概率已知,所以先初始化一种策略,以此策略为基础,利用利用贝尔曼方程迭代求解,让V收敛。这个过程叫策略评估。(注意,贝尔曼方程里的pi(a|s)为固定值,因为策略已经更新了)。
然后根据算好的V,P(s|s,a)[r+gamma*V]这样就计算得到了Q(s,a), 然后从中选取让Q最大的a,固定为策略。这个过程叫策略提升。
反复来回,就叫策略迭代。
N轮策略迭代
意思就是,在迭代过程中,不要求策略评估收敛,只让它迭代固定次数。甚至是1都可以。对于是1 的情况,策略在达到最优之前,价值都不会收敛,所以接近价值迭代。
价值迭代:
不涉及策略,在计算的时候,把不同的策略通通算一遍,选出那个最大的Q来,更新为价值V。在最后收敛完成以后,再根据贝尔曼方程,计算选出最大的Q(s,a)的a来,作为策略。
(价值迭代的速度小于1轮策略迭代,但是比策略迭代的速度块)
广义策略迭代:
在优化的前几轮进行策略迭代,然后进行价值迭代。
蒙特卡罗方法:
不知道环境的状态转移概率的时候,那就必须通过采样才可以。说白了就是希望通过大量采样的方式,更新出q(s,a)来。主要就是依赖剩余时刻的累积reward之和的一个期望,通过大数定理希望采样来估计均值。
那么做法就是倒着算,从结尾开始,一路倒着把reward累加,最后保存到对应的q(s,a)这里。不过这只是一轮的结果。下一轮用其他采样序列又倒着算,又算到这里的时候,通过增量平均的形式,这一时刻的均值=上一时刻的均值+1/N(这一时刻的采样值 - 上一时刻的均值),来不断更新q(s,a),使得q越来越接近真实的期望。
分析:如果所有的都被经历过,蒙特卡罗方法就能很好估计。但是,现实可能并不完美,有些就是很难经历到,缺乏数据,导致估计的不够准确。所以要么就从所有的起点出发采样一遍,要么就采取ε-greedy策略,使得采样数据尽可能的均匀一些,有一定机率能去没去过的地方。
然而蒙特卡洛法估计的方差有一点大,例如在一次采样的同一状态,重复的到达,这个q(s,a)就会被一直更新来更新去,也就是every_visit。所以可以换成first_visit,只统计第一次出现的长期回报。这样的做法可以减小方差,但是效果有限。
为了减小方差,就引入里时序差分法,TD法。
蒙特卡洛法是根据reward反向计算,算出某个q(s,a),然后和原来的q(s,a)用增量平均的形式融合到一起去。
时序差分法是利用相邻时刻的去更新,新的q(s,a)就不再是反向求和起来,而是r(s')和之后的状态的q(s',a')求和,然后把这个作为采样值,和保存的q(s,a)的均值进行增量平均,更新均值。
具体在SARSA和Q-learning在这二者的区别上,SARSA在算新的q(s,a)时,之后的状态是s',就用真实的采样数据的a',进行更新。这样方差就相比蒙特卡洛小了,但是误差会大一点。这个就是On-policy。
但是Q-learning,在计算q(s,a)的时候,不是用的真实后续s'时刻采取的动作a',它用的是q(s',a)里面最大的那个a的值。因为认为后续那个状态里最大的a才能代表q(s,a)的真实的值。这个就是Off-policy。不过可能造成“过高估计”,采样到比较少的地方,就无法“过高估计”,导致产生较大的差距。
分析:如何区分Off-policy和On-policy?上面的说法是一种,更准确的评估方法是,看行动和评估策略是否一致。对于SARSA来说,都是ε-greedy策略。而对Q-learning来说,行动是ε-greedy策略,评估却是贪婪策略。
DQN系列
就是用网络(而不是表格) 来拟合Q函数。
2013版本DQN就只有1个网络,2015版DQN就有俩网络,一个是target网络。target用来暂存参数,就是说我们从target网络中选取让q(s',a)最大的那个a',在target中取q(s',a'),用来更新当前网络,一段时间后再赋值给target网络。
Double_dqn的区别在于,在更新时,在当前网络中选取最大的a,然后把这个a送到target网络中得到Q,更新当前网络。 二者都是从target网络中选取q,但是DQN是从target网络中选a,Double_dqn从当前网络中选a。这个目的是缓解过高估计。(过高估计是因为选择最优行动和计算目标价值使用了相同的参数,所以我们把二者分开)
DQN系列细节
replay buffer:缓存数据,满了以后,就新的来了丢掉旧的。
priority replay buffer: 让有价值的样本频繁出现。所以就用TD-error作为衡量指标,TD-error越高,出现的概率越高。但由于随着参数的更新,TD-error也会变的,所以,希望低Td-error的样本也能出现,所以给td-error弄一个指数,让指数小于1,实现衰减:
为了让更新变的无偏,此外还可以准备一个![]() , 从小于1慢慢变到1,给样本填加权重,
, 从小于1慢慢变到1,给样本填加权重,![]() ,顺便除以最大的,进行归一化。这样加在损失函数上,原先是
,顺便除以最大的,进行归一化。这样加在损失函数上,原先是
![\frac{1}{m}\sum _1^{m}[y-Q]^2](http://img.e-com-net.com/image/info8/620847d76dff48ff907dc305a4edee79.gif) ,现在变为
,现在变为![\frac{1}{m}\sum _1^{m}w_j[y-Q]^2](http://img.e-com-net.com/image/info8/df07311c276f4c5996af8b298be71cb5.gif) 。可以发现,被采样的概率越大,这个权重就越小,作用在损失函数上的比例就越小。这样最后随着
。可以发现,被采样的概率越大,这个权重就越小,作用在损失函数上的比例就越小。这样最后随着![]() 的更新,当
的更新,当![]() 为1的时候,就完全抵消掉priority replay buffer的作用了。
为1的时候,就完全抵消掉priority replay buffer的作用了。
总结:相当于,让更新过程先着重采样Td-error大的那些样本,然后在损失函数那里,逐渐让这些样本占的权重变小,最后让更新从有偏慢慢变得无偏。(前期有偏是因为想快速学习)
Dueling DQN:
在网络上给了更新,网络最后显式的分成了两个输出,一个V,一个A,加起来才是q。Q=V+A。作为优势函数,希望它的均值是0,也就是说不同的q,代表同一个s下采取不同的动作,有的好,有的坏,这个好坏程度就是A,是在V的基础上体现出来的。
另外由于同一个q,有很多V和A组合,都可能得到它,这样就体现不出人为希望V和A具有的实际含义。所以加一个限制,对A减去当前状态下所有A的均值或最大值。例如,当前状态很好,怎样走都很好,那么Q就接近于V,A就接近于均值或者最大值。
最后的效果上,A只对行动相关的内容比较敏感。
DQN冷启动问题:
提高初期学习效率。
1.模仿优质采样轨迹,用监督学习预训练。
2.用多个目标函数:DQN目标函数;N步回报法目标函数(类似结合了N步的蒙特卡洛,再加TD-error),监督学习目标函数,L2正则化目标函数(避免过拟合)。
(注:L1是模型各个参数的绝对值之和。L2是模型各个参数的平方和的开方值。
L1会趋向于产生少量的特征,而其他的特征都是0。因为最优的参数值很大概率出现在坐标轴上,这样就会导致某一维的权重为0 ,产生稀疏权重矩阵。
L2会选择更多的特征,这些特征都会接近于0。 最优的参数值很小概率出现在坐标轴上,因此每一维的参数都不会是0。当最小化||w||时,就会使每一项趋近于0。参数更平滑
这样让模型更简单,减少过拟合。)
Distributional DQN:
这个相当于输出的不是q(s,a)的期望值,而是输出一个分布。即通过softmax输出每一个价值采样点的概率,用概率拟合分布。
那么对应的gt值,是通过公式计算的价值点,(但可能是不对齐的)然后根据距离投影,对齐到网络的输出(原始采样点)上,进行Cross entropy Loss更新。
总结:把模型的输出从计算价值期望改成了计算价值分布。
Noisy Network:另外一种增加探索能力的方法,在参数上增加噪声。
Rainbow:混合了各种思路,把各种网络的特性融合在了一起。
基于策略梯度的算法
策略梯度就是希望轨迹的期望回报最大,也就是它最大:
所以要对它求导,一顿化简,它的导数就化简成了这样:
里面的π(r)对θ求导,一番操作以后,去掉无关的,最后结果就是:
所以求解梯度的最终形式就是:
所以说想让累积回报最大,就是求上面的这个梯度,并且更新参数。
和监督学习的关系:
监督学习,用最大似然,然后求解梯度:
可以看出,RL的策略梯度方法,就是和监督学习,差了一个后面的累积回报。相当于最大似然法把累积回报设定为1,而策略梯度法用序列的回报当作样本的加权权重。
回到策略梯度问题上来,对原先的式子减去一个baseline,是因为区分出正负,让好的策略增大,坏的策略减小。所以再减去一个b,把b设置为均值。
那么整体把r-b当成Adv,那么在实际的计算中,就可以用TD-error的形式,把b用v(s),也就是critic网络的值来代替,r就是采样序列中的![]() 反推累加回去来计算。
反推累加回去来计算。
A2C就是每个线程各自仿真收集数据,然后把数据合在一起更新。A3C是各个线程各自完成参数更新,最后进行融合。
另外,上面的公式,是梯度的表达式,算出梯度以后,进行梯度上升,就能使原函数变大,使得期望变大。
那么原损失函数是什么?原函数的log π(a|s)之前不含有导数符号,因为上面的表达式是导数,不是原函数
策略Loss: ![]()
价值Loss:V(s)和累积反推回去的reward的L2损失
熵Loss:对 π(a|s)求交叉熵,再求负,希望交叉熵足够大,这样模型不确定性高,就会有各种可能。(网络要输出log π(a|s),也就是pi,还要输出v)。比如策略loss中,两个相乘就是这俩相乘。
TRPO:
这个很复杂,这个的思路就是希望新旧策略的差距始终是正的,这样就能保证策略单调非递减的慢慢变好。为了方便计算,用旧策略的概率代替新策略的概率,所以要限制两个策略的距离,所以用KL散度约束。然后用Fisher信息矩阵近似代替KL散度的二阶导数,用自然梯度法去求解。(自然梯度法的概念,是把原先“参数的更新量进行限制”替换成“模型的距离(模型效果)进行限制”。而KL散度不好算,所以用fisher矩阵代替。
步骤很复杂,第一步,计算目标函数梯度 (和PPO其实差不多)
第二步以后,用共轭梯度法求解更新方向,步长,步长上限等……
总之,是希望用旧策略的采样代替新策略的分布,但是发现在一定的区间内才可以。相对PPO是在概率的结果上限制比率,TRPO是在参数上限制。把KL的散度的限制加入到了目标函数中。并用共轭梯度法求解,求方向和步长,并且对其进行限定,即所谓“置信区间”。
GAE:
这个看最后的式子,直观上感觉不好理解。这是因为那个式子是经过了推导得到的。相当于统计了多步的td-error,加入了一个参数λ,它为0的时候,等同于计算Td-drror,它为1的时候,变成了蒙特卡洛目标值 和 价值估计的差。用它来折中,计算结果作为优势函数。
蒙特卡罗的问题在于方差大,而偏差低;
Td-error的问题在于方差小,可偏差高。
这个做法使得二者可以通过系数来折中。
在最上面的策略梯度导数的那个公式那里,(也就是一路把reward累加反推,和V相减,得到Adv的那种做法,其实就相当于是蒙特卡洛,λ=1的情况。
所以其实,Critic值就是优化的是Adv,而Actor,Adv是通过参数传入的,优化的是log π(a|s)。
GAE在实现上可以用倒序计算,
PPO:
然而它不好计算,所以想用蒙特卡洛法来近似,结果就是:
其中old相关的东西都不参与梯度回传,在tensorflow里面都是用placeholder传入的。
TRPO的做法是,对每一轮的优化划定置信区域,而PPO就是直接限制二者的比率,加上双保险:第一轮是限制在[1-ε,1+ε]内,第二轮限制是,选min函数,让clip以后的比率乘以A, 和原始的比率乘以A中再选一个小的数字。(相当于用这种方式来确保算法能达到TRPO的效果)
上面减去KL散度,那么如果KL距离大,这个目标函数就会变小。(而目前是希望目标函数max的)。
那么β就是一个系数,如果KL散度小于阈值,β就/2,缩小,放松KL约束限制。否则增强KL散度限制。
注意:之所以有新概率/旧概率,是因为重要性采样。
求期望,原本是
A(x)就是优势函数,这个已经不能变了,是TD-error,p理解为新的模型,q理解为旧的模型。
问题:看样子是想让td-error变大?? 这个不是误差吗,不应该是变小吗?
回顾:本来是希望从新的模型里采样,让累积reward最大。为了落到正负区域,所以减去一个均值,就是A。
A可以采取很多种形式,TD-error是其中一种。
注意,这里不要和Q-learning相关的混淆,在Q-learning相关内容中,Td-error是要最小,因为模型想分析Q函数。所以用时间差分,把td-error作为误差,使得Q网络分析环境尽可能准确。
而在这里,并不是用的时间差分法。Critic本质上就是对当前s状态下,以后累积reward的均值估计。那么实际采集到的reward,和Critic的输出值,相减才作为td-error。
Actor之所以想让td-error尽可能的大,就是因为在critic固定的情况下,希望尽可能的超过期望。有点GAN网络的意思。
复习的时候好好读一下这段话来理解!
那PPO到底是On-policy还是Off-policy的?
对于第一轮参数更新来说,此时两个网络一模一样,数据也是它采集的,也是它更新的,那毫无疑问就是on-policy的。
对于第二轮参数更新来说,网络不再一样了,可以说是off-policy的。但是,新网络并没有直接根据旧网络的数据来更新自己,而是经过了重要性采样,所以,在这种程度上来说的话,它仍然是on-policy的。
SAC:soft actor critic:
概念就是把熵也加入到奖励函数中,让算法有一定的探索性。
Off-policy 策略梯度法
retrace:
它的作用就是扩展td-error到多步的形式,有点类似GAE,另外还能使用旧数据,避免on-policy要丢掉用过的数据。
以上面的公式为例,cs就是新旧策略的比值,当比值为1,t=0的时候(相当于第一轮),RQ就化简成了TD-error:
所以cs那里连乘,是时间维度上连乘,相当于是每一轮迭代,都能把新旧策略的比值保存下来,以后再用(不像PPO那种,其实就一次,之后就全扔了)。
此外,还限制cs不能超过1。这个作用是限定新旧策略比值,减小重要性采样带来的不稳定性。
ACER:
这一章的内容比较复杂,我也没有什么实践,所以记个大概好了。
ACER的目标是解决on-policy算法样本利用效率低的问题 。
也用replay buffer,但是采样是有顺序的。它的目标是:最大化从交互样本的每一状态出发的长期回报。
流程是:先用On-policy的优化,用当前策略和环境交互采集样本;然后采用off-policy的优化,用保存起来的样本训练。所以replay buffer还要额外保存行动的概率值。retrace则是通过这里的概率值,来计算出一个“考虑了重要性采样”的类似“td-error”,用来更新actor网络。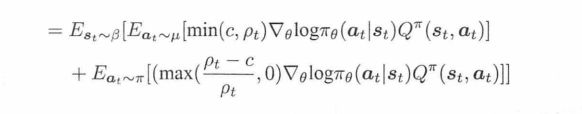
上面这个公式是经过推导得到的,第一项是off-policy的计算,第二项是on-policy部分的计算。第一项是“截断的重要性采样”,限制比率上限,让模型不要太大波动。第二项则是“偏差纠正项”,保证算法是无偏的。作用就是让算法在偏差和方差之间进行了平衡。
c代表着第一项的比率,式子中当C->∞时,相当于使用retrace的off-policy策略梯度更新,当c=0时,相当于Actor-Critic更新,当c不为0的时候相当于介于off-policy和on-policy之间的更新。
这个算法无论理论还是求解过程都比较复杂,应该不会问。
DPG:确定性策略梯度
之前的策略优化可以叫 随机性策略梯度。DPG仍然是对轨迹价值进行求导,但是,它要得到一个确定的行动,而不是PPO那种从概率分布里采样的方式。不采样,但是用ε-greedy方式增加噪声。
DPG就只是这一种思想,化到DDPG上,那就是:先把状态输入到动作网络μ中,然后再把输出的动作和状态一起送入到Q网络中。
这套网络也同样有两个,一个作为target。(每个网络里有两个子网络)
那么动作网络这里涉及到的梯度,就是链式求导,从Q网络的结果那里,求q网络对于输出action的导数,然后action再对输入state的导数,这样来更新μ网络。目标函数则是找到一个好的action,使q大,即目标函数是为了最大化q。
而Q网络则正常使用DQN那种td-error的方法来更新。更新的时候,也是把state输入target网络,输出的结果作为gt值,更新当前网络。
(相当于,DQN那一套,是更新Q网络,输出不同动作的值。在执行的时候,选最大的那个Q。而这里则是把动作和状态一起塞给了Q,借助Q更新的准确,使得动作网络μ也准确,最后可以直接生成一个好的动作。)
另外要注意:
1.更新的时候不是一下子对目标网络赋值,而是很大程度上保留目标网络,只用当前行动网络的参数给它更新一点点。
2.在噪声上,加了一种叫Ornstein-Uhlenbeck噪声。
μ当成网络输出,也作为随机变量的期望。其他的都是参数,W是一个随机函数。真正的采样值,是上一时刻的采样值加上变化量。
其他强化学习算法
稀疏回报的求解方法:
一:层次强化学习:使用元控制器和控制器,由元控制器提供小目标,控制器去努力执行元控制器提供的小目标。例如,在游戏里,元控制器选定小目标区域,使用mask作为单独的通道叠加到图像输入中,再用控制器进行执行。
二:HER,hindsight experience replay,事后诸葛亮。渐进式学习的概念。通过某个操作得到了状态A,那么就保留这个记忆,让模型先学会怎么得到A。相当于逐渐设定可行的目标,让学习难度逐渐平滑。做法就是在replay buffer中,设定一定的概率,将它的目标从原定的目标,换成其他容易实现的目标。
Model-based 方法:
AlphaZero:
在下棋问题上,根据策略计算出有价值的N个招法,相当于裁剪树的宽度;
然后使用价值模型,在深度上进行限制。
MCTS:蒙特卡洛搜索树:
先去选择,根据UCBI(upper confidence bound for tree)的做法,选出价值大或者很少出现的节点(这样来平衡利用和探索)
扩展:根据选择好的节点进行扩展;
模拟:模拟双方招式;
回传:把结果回传给父节点,更新估计值。
所以对于AlphaZero就是三点特征:自我对弈,深层模型,还有一个新旧模型对决(如果新模型下不过旧模型那就不要新模型)
iLQR(iterative linear quadratic regulator)迭代线性二次调节器:这个知识比较老,有点看不懂,大致意思就是通过依时间迭代计算的方式对控制类问题规划求解。
反向强化学习:
如果状态空间有限,最优策略也已经知道,那就无需采样,可以用表格式的方式,直接求解,方式是线性规划。(线性规划的限定里,同时要求某个策略和最优策略接近,但其reward映射还要足够远)
线性规划步骤:
(1)列出约束条件及目标函数
(2)画出约束条件所表示的可行域
(3)在可行域内求目标函数的最优解及最优值
总结就是,先选出和最优策略差距最小的策略,然后使得这两个很相似的策略,在reward上差距变大。
如果状态空间无限大,最优策略知道,那么不能用表格式的方式,就需要通过一个映射函数,把状态映射到低维空间。然后用线性的方式,把状态映射到reward。
为什么要用线性方式映射?是为了后续可以把值函数V也通过线性的方式结合起来,继续用线性规划的方式求解。
如果最优策略不知道,只有最优策略的样本:这种情况就没有次优策略了,让一个随机策略出发采样得到行动轨迹,用之前的做法,计算reward,再用reward进行训练提升策略,迭代进行。
最大熵模型:要求策略的轨迹特征积累量的期望和专家的相等,但又要让熵足够大,从而区别不同的策略。
指数家族,可以把各种指数的分布映射到一个固定的格式。这个的做法让概率分布的期望和方差有了另一种,可能会更简便的计算方法。
GAIL:
其实就是在GAN网络的基础上加上了模仿学习,让评判模型来区分策略模型是专家做法还是自身做法,策略模型就用TRPO算法进行提升,把评判模型的输出作为奖励值。(那么这种做法就不需要学习reward)
其他:例如,在样本选取中,有一定概率选取专家的样本,这也是一种模仿学习,或者示教学习。
纳什均衡是博弈论中一种解的概念,它是指满足下面性质的策略组合:任何一位玩家在此策略组合下单方面改变自己的策略(其他玩家策略不变)都不会提高自身的收益。
V-trace和Retrace类似,只不过Retrace估计的是Q函数,这里估计的是V函数,因此叫V-trace。
IMPALA:Importances Weighted Actor-Learner Architectures,相比于A3C和batched A2C,具有更好的高性能计算性能。Actor和Learner各干各的,谁都不要等谁。Actor们(不只一个)不断地将采到的样本放到Replay Buffer里,并周期性地从Learner那拿到最新的参数。Learner不断地从Replay Buffer里拿样本过来训练自己的参数。要达到这样的目的,也只有off-policy的方法可以这么干了。而如果是on-policy的方法就要遵循:Actor放样本到buffer->Learner取样本训练参数->Actor取最新的参数->Actor执行动作收集样本->Actor放样本到buffer,这个过程按顺序来的,无法并行。