线段树从入门到入土

线段树入门

引题

有一个包含$N$个数的序列($N\le 1e6$)，给$Q(\le 1e6)$个操作，每个操作是下面两种中的一种：

• 区间加：给定$l,r,x$，将序列$N$下标$\in [l,r]$的数加上$x$
• 区间求和：给定$l,r$，询问下标$\in [l,r]$的数的和

一种很暴力的想法是对每个操作都一遍循环进行修改、求和，显然会超时；看到区间求和很容易就能想到前缀和，这样可以把区间求和降到常数复杂度，然而区间加还是$O(N)$；区间加想到差分，然而求和会超时；这时就需要线段树登场了

介绍

线段树是一种实用的数据结构，它可以快速地处理区间操作，维护区间信息。线段树是一棵二叉树，它的每一个节点存储的是一个区间的信息(如区间和, 左右端点等)，如下图所示

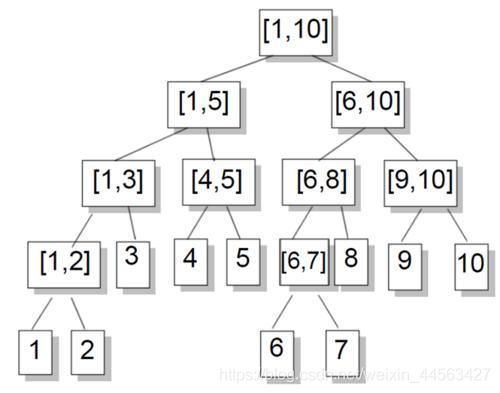
笔者个人比较习惯用结构体来定义每一个节点，如果只开$2N$个节点，有一些情况是不够的，索性开到$4N$，并从上到下，从左向右进行编号，根节点编号为1，其左儿子是2，右儿子是3，一次类推：

#define ls (k << 1) // 左儿子
#define rs (ls | 1) // 右儿子

struct Node {
    int l, r, sum, lazy; // l为左端点，r为端点，sum是区间和, lazy是懒标记下文会讲
    Node() {}
    Node(int _l, int _r, int _sum, int _lazy=0) : l(_l), r(_r), sum(_sum), lazy(_lazy) {}
    inline int length() {return r - l + 1; } // 返回区间长度
    inline ll mi() { return (l + r) >> 1; } // 返回中间点
} node[N << 2];

维护区间信息

每次更新了较低一层的区间信息时，需要维护其父节点的信息，比如区间信息为区间和$sum$时，维护时父节点的$sum$值等于其左右儿子的$sum$值的和

inline update(int k) {
    node[k].sum = node[ls].sum + node[rs].sum;
}

建树

建树从最上一层节点开始向下，一旦遇到叶子节点(区间长度为1的点)，说明到最底层了，则返回，再递归地更新其父节点的区间信息

void build(int l, int r, int k) { // k是编号
    if(l == r) { // 叶子节点，输入它的值并返回
        int a;
        scanf("%d", &a);
        node[k] = Node(l, r, a);
        return ;
    }
    node[k].l = l; node[k].r = r;
    int mid = node[k].mi();
    build(l, mid, ls);
    build(mid + 1, r, rs);
    update(k);
}

区间加

(注意区分等待加的区间$[l,r]$和节点$k$上的区间$[node[k].l,node[k].r]$!!)在区间$[l,r]$上加$addnum$：从根节点开始，如果我们所在的节点的区间$[node[k].l,node[k].r]\subseteq [l,r]$，那么说明这个节点区间的每个值都需要被加$addnum$；否则，说明节点上的区间没有被完全包含在$[l,r]$中，如果$r>mid(mid是节点的区间中值)$，说明区间$[mid+1,r]$这个区间还需要加上$addnum$，所以进入右儿子节点；如果$l<=mid$，说明区间$[l,mid]$这个区间还需要加上$addnum$，所以进入右儿子节点。需要注意的是，后两种情况完全有可能同时满足。我们再仔细考虑区间加，为了维护线段树使其满足左右儿子的$sum$之和等于父节点的$sum$，将父节点的$sum$更新之后应该要把它的所有子节点都更新，再用一下上面的图，比如说我们让$[6,10]$加10，那为了维护线段树，$[6,10]$的子节点们都需要加10，总共需要9次加操作，这造成了一个很严重的问题：这样的区间加甚至比暴力还要慢！一个原本是$O(N)$的操作被我们改进成了$O(NlogN)$，这时，一个重要的思想出现：懒标记。它的思想是先仅维护最上一层的区间信息，而延迟对其子节点的更新，这样做的好处在于可以把区间加累积起来，等有需要时将懒标记下传一次性更新子节点，从而有效降低复杂度

inline void push(int k) { // 懒标记下传
    node[ls].lazy = node[rs].lazy = node[k].lazy;
    node[ls].sum += node[ls].length() * node[k].lazy;
    node[rs].sum += node[rs].length() * node[k].lazy;
    node[k].lazy = 0;
}

inline void add(int k) {
    if(node[k].l >= l && node[k].r <= r) { // 完全包含
        node[k].sum += node[k].length() * addnum;
        node[k].lazy += addnum; // 懒标记
        return ;
    }
    if(node[k].lazy) push(k); // 下传
    if(r > node[k].mid) add(rs);
    if(l <= node[k].mid) add(ls); // 不能是else if
    update(k);
}

区间求和

区间求和的步骤基本和区间加一样，代码也是十分类似

inline ll query(int k) {
    if(node[k].l >= l && node[k].r <= r)
        return node[k].sum;
    ll ans = 0L;
    if(node[k].lazy) push(k);
    if(r > node[k].mi()) ans += query(rs);
    if(l <= node[k].mi()) ans += query(ls);
    return ans;
}

板子

玩整版，开了long long，主要是因为很多题区间一求和就容易爆int

#include 
#include 
#include 
#define mid ((l + r) >> 1)
#define ls (k << 1)
#define rs (k << 1 | 1)
typedef long long ll;
const int N = 1e6+5;

struct Node {
    ll l, r, sum, lazy;
    Node() {}
    Node(ll _l, ll _r, ll _sum, ll _lazy = 0L) : l(_l), r(_r), sum(_sum), lazy(_lazy) {}
    inline ll length() { return r - l + 1; }
    inline ll mi() { return (l + r) >> 1; }
}node[N << 2];

ll n, m, l, r, addnum;

inline ll read() { // 快读
    ll x = 0;
    char ch = getchar();
    while(ch < '0' || ch > '9')
        ch = getchar();
    while(ch >= '0' && ch <= '9') {
        x = (x << 3) + (x << 1) + (ch ^ 48);
        ch = getchar();
    }
    return x;
}

inline void update(int k) {
    node[k].sum = node[ls].sum + node[rs].sum;
}

inline void push(int k) {
    node[ls].lazy += node[k].lazy;
    node[rs].lazy += node[k].lazy;
    node[ls].sum += node[k].lazy * node[ls].length();
    node[rs].sum += node[k].lazy * node[rs].length();
    node[k].lazy = 0L;
}

void build(int l, int r, int k) {
    if(l == r) {
        ll a = read();
        node[k] = Node(l, r, a);
        return ;
    }
    node[k].l = l; node[k].r = r;
    build(l, mid, ls);
    build(mid + 1, r, rs);
    update(k);
}

inline void add(int k) {
    if(node[k].l >= l && node[k].r <= r) {
        node[k].sum += node[k].length() * addnum;
        node[k].lazy += addnum;
        return ;
    }
    if(node[k].lazy) push(k);
    if(r > node[k].mi()) add(rs);
    if(l <= node[k].mi()) add(ls);
    update(k);
}

inline ll query(int k) {
    if(node[k].l >= l && node[k].r <= r)
        return node[k].sum;
    ll ans = 0L;
    if(node[k].lazy) push(k);
    if(r > node[k].mi()) ans += query(rs);
    if(l <= node[k].mi()) ans += query(ls);
    return ans;
}

int main() {
    n = read(), m = read();
    build(1L, n, 1L);
    while(m--) {
        ll type;
        type = read(); l = read(), r = read();
        if(type == 2L) // 区间查询
            printf("%lld\n", query(1L));
        else if(type == 1L) { // 区间加
            addnum = read();
            add(1L);
        }
    }
    return 0;
}

各种类型

最基础的几种

• 区间加 + 区间求和，这是最基本的线段树，板子题luogu 3372

• 区间乘 + 区间求和，其实像维护加法懒标记一样，再维护一个乘法的懒标记就可以了，再稍微改改懒标记下传，板子题luogu 3373

• 区间修改 + 区间求最值，如果没有区间修改，那打个ST就行了(不知道ST的话可以百度一下，很多博客都讲得很清楚)，常数还小，有修改就用线段树就行，维护也很简单，取个max就行了

区间加 + 区间求平方之和(或者立方之和)

$$\begin{gathered} (a_i+x{)}^2=a_i^2+2x\ast a_i+x^2 \\ \sum _{i=l}^r((a_i+x{)}^2)=\sum _{i=l}^r{a}_i^2+2x\ast \sum _{i=l}^r{a}_i+(l-r+1)\ast x^2 \end{gathered}$$

可以按照上面的公式维护$\sum a_i$和$\sum a_i^2$，立方类似，题目HDU 4578 Transformation

区间开根号(向下取整) + 区间求和

开根号操作会让区间里的值变得更加接近，那只要维护区间$max$，如果$max\ne 1$，就暴力地把这个区间上的数都开方，且因为一个数$n$最多被开方$logn$次就会变成1，所以每个数暴力其实最多$O(logn)$，不会超时

• HDU 4027 Can you answer these queries?

例题

然而线段树的很多题都结合了各种技巧，如下面这道：

• POJ 2528 Mayor’s posters

  思路：离散化+线段树

• HDU 2795 Billboard

  思路：我们把高度那一维当做线段树的区间进行建树，然后维护区间最大值，询问时先判断能不能贴上，即根节点的最大值和$width$比较，然后优先向左儿子走，如果左儿子的最大值大于等于$width$，就进左儿子；否就进右儿子，到叶子节点就输出。可是，$h$的数据范围是$1e9$，如果直接这样存线段树绝对爆空间，而我们发现其实$n$的数据量只有$2e5$，而$h$超过$n$是没有必要的，我们只需要最靠上的广告位，所以如果$h>n$，就让$h=n$，这样就完成了这题