中文分词:隐马尔可夫-维特比算法(HMM-Viterbi)附源码
目录
0、先验知识
1、什么是中文分词
2、数据集的构造
3、训练及预测过程简述
4、训练阶段:统计隐马尔可夫模型的参数
5、预测阶段:应用 Viterbi 算法
6、完整的 Python 实现代码
0、先验知识
有关隐马尔科夫模型(HMM)可以查看:
马尔可夫链 以及 隐马尔可夫模型(HMM)_Flag_ing的博客-CSDN博客![]() https://blog.csdn.net/Flag_ing/article/details/123123575?spm=1001.2014.3001.5502有关 维特比(Viterbi)算法可以查看:
https://blog.csdn.net/Flag_ing/article/details/123123575?spm=1001.2014.3001.5502有关 维特比(Viterbi)算法可以查看:
Viterbi算法(维特比算法)_Flag_ing的博客-CSDN博客![]() https://blog.csdn.net/Flag_ing/article/details/123123660?spm=1001.2014.3001.5502中文分词数据集下载链接:icwb2-data中文分词数据集 - 数据集下载 - 超神经 (hyper.ai)
https://blog.csdn.net/Flag_ing/article/details/123123660?spm=1001.2014.3001.5502中文分词数据集下载链接:icwb2-data中文分词数据集 - 数据集下载 - 超神经 (hyper.ai)
1、什么是中文分词
与英文句子这样天生就是用空格隔开的构造不同,中文语句是连贯的,中文分词就是把连贯的中文语句拆分成分离的词语。要想让机器理解中文句子的关键信息,很多情况下需要对句子做分词处理。
比如对中文语句“很高兴遇到你。”这句话进行分词的结果就是“很_高兴_遇到_你_。”,一般来说,中文分词的结果不是唯一的,因为有些字可以认为独立成词,也可以与别的字连贯成词。
2、数据集的构造
中文分词数据集一般都是人工标注的,如下图所示。每行都是一句话,相应的词语已经用空格隔开。
有了这些原始数据集,我们需要给他们打上标签(对应 HMM 中的隐藏状态),相当于做一个映射。可以根据个人喜好给每个词语打上标签,举个例子:
个词语开头的字可以用数字“0”代替,中间的字统统用数字“1”代替,结尾的字用数字“2”代替,如果是一个字或者标点等单独成词的话就用数字“3”代替。比如词“满怀信心”的标签就是“0112”,对于单独成词的“我”的标签就是“3”。由已分好的词可以得到相应的状态链,反过来由一条语句的状态链可以得到这条语句的分词结果。
3、训练及预测过程简述
数据集的训练过程就是得到 HMM 的转移矩阵 A、观测概率矩阵 B、初始状态概率矩阵 ![]() 的过程,如下图所示。
的过程,如下图所示。
模型的预测过程就是输入观测向量 O(观测序列)得到状态序列 I(分词结果)的过程,如下图所示。
以下分别介绍相关矩阵的获取。
4、训练阶段:统计隐马尔可夫模型的参数
在训练阶段,三个矩阵的获取都较为简单
- 初始状态概率矩阵

该矩阵就是统计所有语句的开始第一个字的状态分布,根据前述,一共只能有两种可能的状态,即一个词的开始状态“0”或单独成词状态“3”,统计出所有训练集中的开始字的根部状态概率即可,结果为一个 ![]() 的向量[p,0,0,1-p]。
的向量[p,0,0,1-p]。
- 状态转移概率矩阵 A
统计训练集中每条语句每个词语的状态转移情况,最终归一化为概率,结果是一个 ![]() 的矩阵。注意该矩阵每行的概率和为1,以及确定转移概率为 0 的位置,可用来检查训练结果。
的矩阵。注意该矩阵每行的概率和为1,以及确定转移概率为 0 的位置,可用来检查训练结果。
- 观测概率矩阵 B
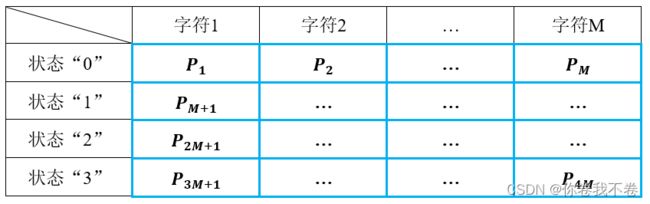
统计四种状态中每个汉字及标点在每种状态下出现的次数,最终以行为单位进行归一化。假设汉字和标点共有 M 个,最终结果是一个 ![]() 的矩阵
的矩阵
得到上述三个矩阵后训练阶段就完成了,可以看出,训练阶段其实就是对训练集数据做一个简单的统计。
接下来讲解如何使用训练出来的三个矩阵并利用Viterbi算法进行语句分词的预测。
5、预测阶段:应用 Viterbi 算法
以输入一条语句“很高兴遇到你”为例,用 HMM 图形化表示如下图:
图中状态序列就是理想输出结果,观测序列就是我们的输入语句,根据马尔可夫模型![]() 预测的状态序列即可得出最终的分词结果。这个过程称作解码。
预测的状态序列即可得出最终的分词结果。这个过程称作解码。
在使用维特比算法解码过程中需要计算两个矩阵,下面分别介绍。
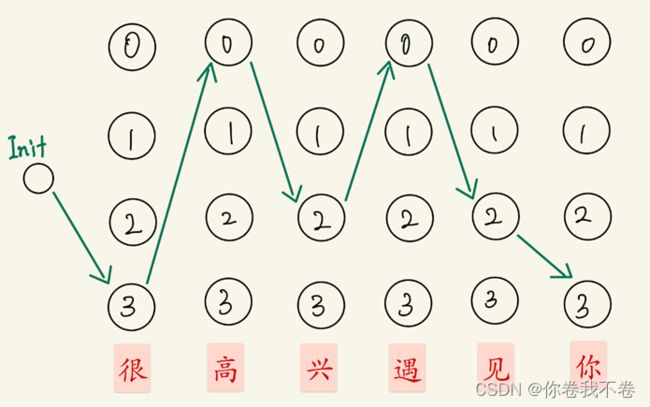
首先画出“很高兴遇到你”的状态转移图如下,图中已画出最优的状态连接。
计算图示路线概率的方法如下
由前述维特比算法的过程可知,图中最终会留下4条候选路径。如果想存储 状态转移图 中的信息,则需要两个矩阵:
1、一个![]() 矩阵D存储路线的连接方式
矩阵D存储路线的连接方式
2、一个 ![]() 的矩阵P存储矩阵 D 中对应路线的概率。
的矩阵P存储矩阵 D 中对应路线的概率。
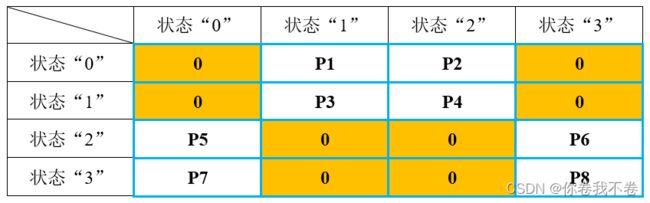
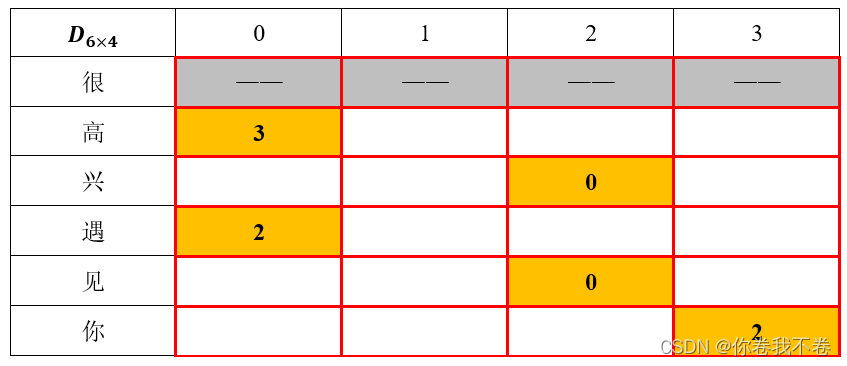
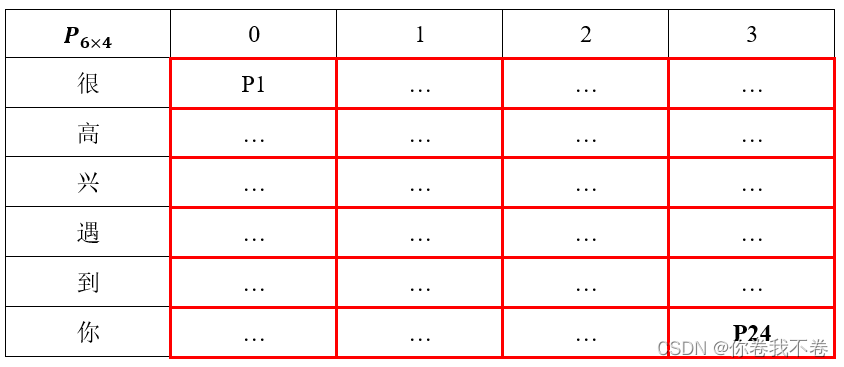
第一个矩阵 ![]() 存储候选路径的连接方向。状态转移图 的示例线路的存储方式见下表,如何理解这个矩阵呢?把上述 状态转移图 顺时针旋转90度就是了。
存储候选路径的连接方向。状态转移图 的示例线路的存储方式见下表,如何理解这个矩阵呢?把上述 状态转移图 顺时针旋转90度就是了。
例如。P[1,0]=3代表字符“高”的状态“0”最有可能是字符“很”的状态“3”转移来的,对应着 状态转移图 中字符“很”的状态“3”连接字符“高”的状态“0”。
另一个矩阵 ![]() 存储候选路线的概率。每行代表依次输入语句中的一个字符,每列代表该字符所处的状态。这里的概率对应矩阵 D 相应连线上的概率。第一行的概率由初始状态 Π 与观测矩阵 B 计算得来,接下来的每一行由上一行通过转移矩阵 A 与观测矩阵 B 计算得来。
存储候选路线的概率。每行代表依次输入语句中的一个字符,每列代表该字符所处的状态。这里的概率对应矩阵 D 相应连线上的概率。第一行的概率由初始状态 Π 与观测矩阵 B 计算得来,接下来的每一行由上一行通过转移矩阵 A 与观测矩阵 B 计算得来。
例如,P[1,0]位置代表字符“很”的状态“3”连接到字符“高”的状态“0”的概率,而这个概率正是由字符“很”的4个状态与字符“高”的状态“0”的四种连接方式中挑出来的最高的那个。
有了上述两个矩阵就可以通过回溯来找出最优路径了:首先找出矩阵 P 最后一行的最大值,这个最大值就是最优路径的概率,该最大值的索引位置就是最后一个字符“你”的状态位,然后再矩阵 D 中找出相应位置的状态,这个 D 中的状态就是字符“你”所连接的上一个字符“到”的状态,此时矩阵 P 就结束了使命,接下来继续在矩阵 D 中向前回溯即可得到最终的最优状态链,根据该状态链就可以的出相应的分词结果。
有了上述 HMM—Viterbi 实现中文分词的原理及过程,就可以通过编程实现了。
6、完整的 Python 实现代码
使用时注意修改相应的 文件路径
import numpy as np
## 将原始文字信息转换为状态信息,并返回
def text_to_state(line):
# 状态列表
state = []
# 除去首尾的空格,并以空格分割出各个词语
words = line.strip().split()
for word in words:
# 获取词语长度
word_len = len(word)
if word_len:
if word_len == 1: # 单独成词
state.append(3)
elif word_len == 2:
state.append(0)
state.append(2)
else:
state.append(0)
for i in range(word_len-2):
state.append(1)
state.append(2)
temp = []
for s in words:
for c in s:
temp.append(c)
words = temp
return words, state
# 定义隐马尔科夫模型
class HMM(object):
def __init__(self, train_text_file='train_data\\pku_training.txt'):
# 训练集文件路径
self.train_file_path = train_text_file
# 定义转移概率矩阵
self.A = np.zeros((4, 4))
# 定义观测概率矩阵
self.B = np.zeros((4, 65536))
# 定义初始化矩阵
self.pi = np.zeros(4)
# 根据训练集训练A、B、pi矩阵
self.count_A_B_pi()
self.A_B_pi_normalized()
def count_A_B_pi(self):
# 逐行读取文件
for line in open(self.train_file_path, encoding='utf-8').readlines():
# 提取汉字及对应的状态信息
words, state = text_to_state(line)
for i in range(len(words)):
# 统计 pi
if i == 0:
self.pi[state[0]] += 1
# 统计 A
if i <= len(words) - 2:
self.A[state[i], state[i+1]] += 1
# 统计 B
self.B[state[i], ord(words[i])] += 1
# 加 1e-6 为了避免后面出现 log0 的情况
self.A += 1e-6
self.B += 1e-6
self.pi += 1e-6
def A_B_pi_normalized(self):
# 由于概率一般会很小,这里将最后结果都取对数,对应后面的概率乘积变为加和
# pi 归一化
self.pi = np.log10(self.pi / np.sum(self.pi))
# A 归一化
for i in range(len(self.A)):
self.A[i, :] = np.log10(self.A[i, :] / np.sum(self.A[i, :]))
# B 归一化
for i in range(len(self.B)):
self.B[i, :] = np.log10(self.B[i, :] / np.sum(self.B[i, :]))
print(self.B)
def viterbi(A, B, pi, sentence):
N = len(sentence)
# 定义路径概率矩阵 P,存储候选路线的概率,大小为 (N, 4),N为句子中的字符数。
# 比如,P[1,0] 位置上的值代表 句子中第0个字符 的 四种状态中 最有可能连接到 句子中第1个字符 的 状态“0” 的(最大)概率,
# 而这个概率正是由 句子中第0个字符 的4个状态与 句子中第1个字符 的状态“0”的四种连接方式中挑出来的最高的那个。
P = np.zeros((N, 4))
# 定义路径连接矩阵 D,存储候选路径的连接方向,大小为 (N, 4),N为句子中的字符数。
# 若 P[1,0]=3 ,代表 句子中第1个字符 的状态“0”最有可能是 句子中第0个字符 的状态“3”转移来的,对应着 句子中第0个字符 的状态“3”连接 句子中第1个字符 的状态“0”
D = np.zeros((N, 4))
# 由初始概率矩阵 pi 及 观测概率矩阵 B 计算 P[0, :],即句子开头的字属于四种状态的概率
for i in range(4):
P[0, i] = pi[i] + B[i, ord(sentence[0])]
# 由 概率转移矩阵 A 及 观测概率矩阵 B 计算 矩阵 D 及矩阵 P 剩下的部分
for n in range(N - 1):
# 存储后一个字符的某个状态与前一个字符的所有状态的四种连接概率
prob_temp = np.zeros(4)
for i in range(4):
for j in range(4):
# (第 n 个字的状态 j) 转移到 (第 n+1 个字的状态 i) 的概率。
# 计算方式:(第 n 个字状态 j 的概率) 乘以 (状态 j 转移到状态 i 的概率) 乘以 (状态 i 下是第 n+1 个字的概率)。
prob_temp[j] = P[n, j] + A[j, i] + B[i, ord(sentence[n+1])]
# 计算 prob_temp 的最大值及最大值的索引
max_prob, index = np.max(prob_temp), np.argmax(prob_temp)
# print (max_prob)
# print (index)
# D 赋值: (第n+1 个字的第 i 个状态) 连接到 (第 n 个字的 第 index 个状态)
D[n+1, i] = index
# P 赋值: (第n+1 个字的第 i 个状态) 连接到 (第 n 个字的 第 index 个状态) 的概率
P[n+1, i] = max_prob
# print(P)
# print(D)
# 回溯
path = []
to_next = np.argmax(P[-1, :])
path.append(to_next)
for i in range(N-1, 0, -1): # N-1 ~ 1
to_next = D[i, int(to_next)]
# print(to_next)
path.append(int(to_next))
path.reverse()
# 返回分词结果
return path
if __name__ == "__main__":
# 读取训练文件,并初始化(训练) HMM 参数
hmm = HMM('train_data\\pku_training.txt')
# 测试用例
sentence = "怎么是北京大学的数据集呢?你猜猜,我不告诉你,哈哈哈"
# 应用 viterbi 算法
state_chain = viterbi(hmm.A, hmm.B, hmm.pi, sentence)
print(state_chain)
# 根据状态链进行分词
out = ''
for i in range(len(state_chain)):
if i == 0:
out = out + sentence[i]
if state_chain[0] == 3:
out += ' '
elif state_chain[i] == 0 or state_chain[i] == 1:
out += sentence[i]
elif state_chain[i] == 2 or state_chain[i] == 3:
out += sentence[i]
out += ' '
# 打印结果
print(out)
# 保存结果为 txt 文件
outfile = open("out.txt", 'w', encoding='utf-8')
outfile.write(out)
# 关闭文件
outfile.close()