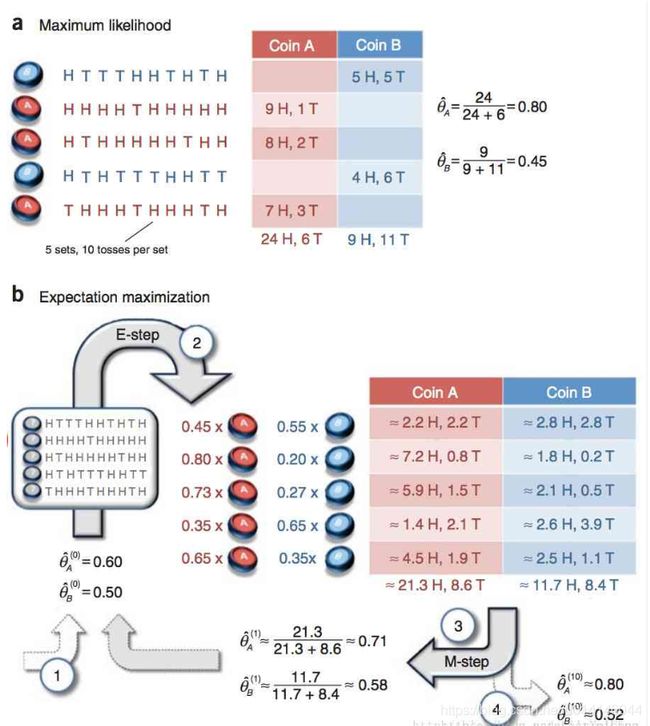
EM算法实现双硬币模型(python实现)
EM(Expectation-Maximization)算法可以对结果进行预测参数的信息,在一些含有隐变量的参数中使用它可以对模型参数进行一定的估计,并且它在机器学习的很多领域都会运用,这里我用python实现双硬币模型。
import numpy as np
import math
mp = math.pow
class EM:
def __init__(self, theta):
self.theta_ap,self.theta_bp = theta
self.theta_an = 1 - self.theta_ap
self.theta_bn = 1 - self.theta_bp
info_array = np.array([[1,0,0,0,1,1,0,1,0,1],
[1,1,1,1,0,1,1,1,1,1],
[1,0,1,1,1,1,1,0,1,1],
[1,0,1,0,0,0,1,1,0,0],
[0,1,1,1,0,1,1,1,0,1]]) #硬币正反的信息
#计算时为了方便加入的算子
self.assist_array = np.ones(10)
self.add_array = np.ones(5)
self.help_array = np.array([10,-1]) #计算向下硬币的矩阵算子
self.mul = np.array([0.1]) #向上或向下的概率矩阵算子
self.up_array=np.matmul(info_array,self.assist_array.T) #向上的硬币个数矩阵
self.calc_array = np.column_stack((self.add_array,self.up_array))
self.down_array = np.inner(self.calc_array,self.help_array) #向下的硬币个数矩阵
self.probility_array_a = np.zeros(5) #属于A的概率
self.probility_array_b = np.zeros(5) #属于B的概率
self.pa = np.zeros(5) #P(z = A|y1,theta_a)
self.pb = np.zeros(5) #P(z = B|y1,theta_a)
self.proportion_up = np.zeros(5) #向上的硬币占比
self.proportion_down = np.zeros(5) #向下的硬币占比
self.upgrade_array = np.zeros((2,2)) #概率更新矩阵
self.proportion_up = self.up_array.T*self.mul #向上的硬币占比
self.proportion_down = self.down_array.T*self.mul #向下的硬币占比
def e_step(self):
for i in range(5):
self.pa[i]=mp(self.theta_ap,self.up_array[i])*mp(self.theta_an,self.down_array[i])
self.pb[i]=mp(self.theta_bp,self.up_array[i])*mp(self.theta_bn,self.down_array[i])
for i in range(5):
self.probility_array_a[i] = self.pa[i]/(self.pa[i]+self.pb[i])
self.probility_array_b[i] = 1 - self.probility_array_a[i]
mul_unit = np.row_stack((self.proportion_up,self.proportion_down))
probility_unit = np.column_stack((self.probility_array_a,self.probility_array_b))
self.upgrade_array = np.dot(mul_unit,probility_unit) #更新概率矩阵
def m_step(self):
self.theta_ap = self.upgrade_array[0,0]/(self.upgrade_array[0,0]+ self.upgrade_array[1,0]) #更新theta_a
self.theta_an = 1 - self.theta_ap
self.theta_bp = self.upgrade_array[0,1]/(self.upgrade_array[0,1]+ self.upgrade_array[1,1]) #更新theta_b
self.theta_bn = 1 - self.theta_bp
#进行下一轮迭代
print(self.upgrade_array)
print(self.theta_ap)
print(self.theta_bp)
def em_algo(self):
for i in range(20):
self.e_step()
self.m_step()
def main():
f = EM(theta=[0.6,0.5])
f.em_algo()
if __name__ == "__main__":
main()
这里尽量使用矩阵运算来代替循环,因此涉及到矩阵运算,而且矩阵运算可以利用GPU进行加速,在大型项目中使用较多。
结果为:
[[2.12974819 1.17025181]
[0.85722466 0.84277534]]
0.7130122354005162
0.5813393083136625
[[1.92093824 1.37906176]
[0.65649201 1.04350799]]
0.7452920360819947
0.5692557501718727
[[1.94102768 1.35897232]
[0.5860269 1.1139731 ]]
0.7680988343673211
0.5495359141383477
[[1.97538329 1.32461671]
[0.54692598 1.15307402]]
0.7831645842999735
0.5346174541475203
[[1.99753285 1.30246715]
[0.52761677 1.17238323]]
0.7910552458637526
0.5262811670299319
[[2.00879016 1.29120984]
[0.51947654 1.18052346]]
0.7945325379936993
0.5223904375178747
[[2.01398202 1.28601798]
[0.5163729 1.1836271 ]]
0.7959286672497985
0.5207298780860258
[[2.01628374 1.28371626]
[0.51525515 1.18474485]]
0.7964656379225264
0.5200471890029876
[[2.0172865 1.2827135 ]
[0.51486707 1.18513293]]
0.7966683078984393
0.5197703896938074
[[2.01771917 1.28228083]
[0.51473641 1.18526359]]
0.7967441494752115
0.5196586622041123
最终结果为A向上的概率为0.79,B向上的概率为0.52.