最小-最大搜索
Bruce Moreland / 文
从浅显的地方开始
在国际象棋里，双方棋手都知道每个棋子在哪里，他们轮流走并且可以走任何合理的着法。下棋的目的就是将死对方，或者避免被将死，或者有时争取和棋是最好的选择。 国际象棋程序通过使用“搜索”函数来寻找着法。搜索函数获得棋局信息，然后寻找对于程序一方来说最好的着法。 一个浅显的搜索函数用“树状搜索”(Tree-Searching)来实现。一个国际象棋棋局通常可以看作一个很大的n叉树(“n叉树”意思是树的每个结点有任意多个分枝通向其他结点)，棋盘上目前的局面就是“根局面”(Root Position)或“根结点”(Root Node)。从根局面走一步棋，局面就到达根局面的“分枝”(Branch)，这些局面称为“后续局面”(Successor Position)或“后续结点”(Successor Nodes)。每个后续局面后面还有一系列分枝，每个分枝就是这个局面的一个合理的着法。 国际象棋的树非常庞大(通常每个局面有35个分枝)，又非常深。 每盘棋局都是一棵巨大的n叉树，如果能通过树状搜索找到棋局中对双方来说都最好的着法就好了。这个浅显的算法在这里称为“最小-最大搜索”(Min-max Search)。 用最小-最大搜索来解诸如井字棋的简单棋局是可行的(即完全了解每一种变化)。井字棋的博弈树既不烦琐也不深，所以整个树可以遍历，棋局的所有变化都可以知道，任何局面都可以保证找到一步最佳着法。 数学上用这种方法处理国际象棋也是可以的，但是目前和不久的将来用计算机去实现，却是不可行的。即便如此，我们仍然可以用基于最小-最大搜索的程序来下国际象棋。相比最小-最大地搜索整个树，在一个给定的局面下搜索前几步则是可能的。由于叶子结点的局面没能搜索出杀棋或和棋，所以要用一个称为“评价”(Evaluate)的启发函数给这些局面赋值。尽管程序设计师希望这些值能够通过知识来得到，但它们确实都是猜的。 基于最小-最大的评价函数 我不打算在这里谈很多关于评价函数的细节。这里我只说明它是怎样确定的，在以后的章节中会详细展开。评价函数首先应该返回局面的准确值，在没办法得到准确值的情况下，如果可能的话启发值也可以。它可以由两种方法来决定： (1) 如果黑方被将死了，那么评价函数返回一个充分大的正数；如果白方被将死了，那么返回一个充分大的负数；如果棋局是和棋(例如某一方逼和，或者双方都只有王)，那么返回一个常数，通常是零或接近零。如果不是棋局结束局面，那么它返回一个启发值。我将不详细介绍这个启发值是如何确定的，但是我有把握说子力平衡是首先要考虑的(如果白方盘面上多子的话，这个值就大)，而其他位置上的考虑(兵型、王的安全性、重要的子力等等)也需要加上。如果白方是赢棋或者很有希望赢，那么启发函数通常会返回正数；如果黑方是赢棋或者很有希望赢，那么返回负数；如果棋局是均势或者是和棋，那么返回在零左右的数值。 (2) 这个函数的工作原理跟第一个一样，只是如果当前局面要走子的一方优势，那么它返回正数，反之是负数。 最小-最大搜索是如何运作的 最小-最大搜索是一对几乎一样的函数，或者说两个逻辑上重复的函数。我写了很少的代码，用一个更好的函数来完成同一件事，但是写出来时却收到一些意见，因此我首先写出纯粹的(不完美的)最小-最大函数，代码如下：
int MinMax(int depth) {
if (SideToMove() == WHITE) { // 白方是“最大”者
return Max(depth);
} else { // 黑方是“最小”者
return Min(depth);
}
}
int Max(int depth) {
int best = -INFINITY;
if (depth <= 0) {
return Evaluate();
}
GenerateLegalMoves();
while (MovesLeft()) {
MakeNextMove();
val = Min(depth - 1);
UnmakeMove();
if (val > best) {
best = val;
}
}
return best;
}
int Min(int depth) {
int best = INFINITY; // 注意这里不同于“最大”算法
if (depth <= 0) {
return Evaluate();
}
GenerateLegalMoves();
while (MovesLeft()) {
MakeNextMove();
val = Max(depth - 1);
UnmakeMove();
if (val < best) { // 注意这里不同于“最大”算法
best = val;
}
}
return best;
}
上面的代码可以这样调用：
val = MinMax(5);
这样可以返回当前局面的评价，它是向前看5步的结果。 这里的“评价”函数用的是我上面所说第一种定义，它总是返回对于白方来说的局面。 我简要描述一下这个函数是如何运作的。假设根局面(棋盘上当前局面)是白方走，那么调用的是“Max”函数，它产生白方所有合理着法。在每个后续局面中，调用的是“Min”函数，它对局面作出评价并返回。由于现在是白走，因此白方需要让评价尽可能地大，能得到最大值的那个着法被认为是最好的，因此返回这个着法的评价。 “Min”函数正好相反，当黑方走时调用“Min”函数，而黑方需要尽可能地小，因此选择能得到最小值的那个着法。 这两个函数是互相递归的，即它们互相调用，直到达到所需要的深度为止。当函数到达最底层时，它们就返回“Evaluate”函数的值。 如果在深度为1时调用“MinMax”函数，那么“Evaluate”函数在走完每个合理着法之后就调用，选择一个能达到最佳值的那个着法导致的局面。如果层数大于1，那么另一方有权选择局面，并找一个最好的。 以上内容应该不难理解，但是代码很长，下面有个更好的办法。 负值最大函数 负值最大只是对最小-最大的优化，“评价”函数返回我所说的第二种定义，对于当前结点上要走的一方，占优的情况返回正值，其他结点也是对于要走的一方而言的。这个值返回后要加上负号，因为返回以后就是对另一方而言了。代码如下：
int NegaMax(int depth) {
int best = -INFINITY;
if (depth <= 0) {
return Evaluate();
}
GenerateLegalMoves();
while (MovesLeft()) {
MakeNextMove();
val = -NegaMax(depth - 1); // 注意这里有个负号。
UnmakeMove();
if (val > best) {
best = val;
}
}
return best;
}
在这个函数里，当走子一方改变时就要对返回值取负值，以反映当前局面评价的更改。就根结点是白先走的情况，如果没有剩下的层数，那么“评价”返回的值是就白方而言的，如果有剩下的层数，就产生后续局面，函数对这些局面逐一做递归，每个次递归都得到就黑方而言的评价，黑方走得越好值就越大。当评价值返回时，它们被取负数，变成就白方而言的评价。 该函数在遍历时结点的顺序同“最小-最大”搜索的函数是一样的，产生的返回值也一样。它的代码更短，同时减少了移植代码时出错的可能，代码维护起来也比较方便。 原文：http://www.seanet.com/~brucemo/topics/minmax.htm 译者：象棋百科全书网 ([email protected])
类型：全译
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
Alpha-Beta搜索
Bruce Moreland / 文
最小-最大的问题 Alpha-Beta 同“最小-最大”非常相似，事实上只多了一条额外的语句。最小最大运行时要检查整个博弈树，然后尽可能选择最好的线路。这是非常好理解的，但效率非常低。每次搜索更深一层时，树的大小就呈指数式增长。 通常一个国际象棋局面都有35个左右的合理着法，所以用最小-最大搜索来搜索一层深度，就有35个局面要检查，如果用这个函数来搜索两层，就有352个局面要搜索。这就已经上千了，看上去还不怎样，但是数字增长得非常迅速，例如六层的搜索就接近是二十亿，而十层的搜索就超过两千万亿了。 要想通过检查搜索树的前面几层，并且在叶子结点上用启发式的评价，那么做尽可能深的搜索是很重要的。最小-最大搜索无法做到很深的搜索，因为有效的分枝因子实在太大了。 口袋的例子 幸运的是我们有办法来减小分枝因子，这个办法非常可靠，实际上这样做绝对没有坏处，纯粹是个有益的办法。这个方法是建立在一个思想上的，如果你已经有一个不太坏的选择了，那么当你要作别的选择并知道它不会更好时，你没有必要确切地知道它有多坏。有了最好的选择，任何不比它更好的选择就是足够坏的，因此你可以撇开它而不需要完全了解它。只要你能证明它不比最好的选择更好，你就可以完全抛弃它。 你可能仍旧不明白，那么我就举个例子。比如你的死敌面前有很多口袋，他和你打赌赌输了，因此他必须从中给你一样东西，而挑选规则却非常奇怪： 每个口袋里有几件物品，你能取其中的一件，你来挑这件物品所在的口袋，而他来挑这个口袋里的物品。你要赶紧挑出口袋并离开，因为你不愿意一直做在那里翻口袋而让你的死敌盯着你。 假设你一次只能找一只口袋，在找口袋时一次只能从里面摸出一样东西。 很显然，当你挑出口袋时，你的死敌会把口袋里最糟糕的物品给你，因此你的目标是挑出“诸多最糟的物品当中是最好的”那个口袋。 你很容易把最小-最大原理运用到这个问题上。你是最大一方棋手，你将挑出最好的口袋。而你的死敌是最小一方棋手，他将挑出最好的口袋里尽可能差的物品。运用最小-最大原理，你需要做的就是挑一个有“最好的最差的”物品的口袋。 假设你可以估计口袋里每个物品的准确价值的话，最小-最大原理可以让你作出正确的选择。我们讨论的话题中，准确评价并不重要，因为它同最小-最大或Alpha-Beta的工作原理没有关系。现在我们假设你可以正确地评价物品。 最小-最大原理刚才讨论过，它的问题是效率太低。你必须看每个口袋里的每件物品，这就需要花很多时间。 那么怎样才能做得比最小-最大更高效呢？ 我们从第一个口袋开始，看每一件物品，并对口袋作出评价。比方说口袋里有一只花生黄油三明治和一辆新汽车的钥匙。你知道三明治更糟，因此如果你挑了这只口袋就会得到三明治。事实上只要我们假设对手也会跟我们一样正确评价物品，那么口袋里的汽车钥匙就是无关紧要的了。 现在你开始翻第二个口袋，这次你采取的方案就和最小-最大方案不同了。你每次看一件物品，并跟你能得到的最好的那件物品(三明治)去比较。只要物品比三明治更好，那么你就按照最小-最大方案来办——去找最糟的，或许最糟的要比三明治更好，那么你就可以挑这个口袋，它比装有三明治的那个口袋好。 比方这个口袋里的第一件物品是一张20美元的钞票，它比三明治好。如果包里其他东西都没比这个更糟了，那么如果你选了这个口袋，它就是对手必须给你的物品，这个口袋就成了你的选择。 这个口袋里的下一件物品是六合装的流行唱片。你认为它比三明治好，但比20美元差，那么这个口袋仍旧可以选择。再下一件物品是一条烂鱼，这回比三明治差了。于是你就说“不谢了”，把口袋放回去，不再考虑它了。 无论口袋里还有什么东西，或许还有另一辆汽车的钥匙，也没有用了，因为你会得到那条烂鱼。或许还有比烂鱼更糟的东西(那么你看着办吧)。无论如何烂鱼已经够糟的了，而你知道挑那个有三明治的口袋肯定会更好。 算法 Alpha-Beta就是这么工作的，并且只能用递归来实现。稍后我们再来谈最小一方的策略，我希望这样可以更明白些。 这个思想是在搜索中传递两个值，第一个值是Alpha，即搜索到的最好值，任何比它更小的值就没用了，因为策略就是知道Alpha的值，任何小于或等于Alpha的值都不会有所提高。 第二个值是Beta，即对于对手来说最坏的值。这是对手所能承受的最坏的结果，因为我们知道在对手看来，他总是会找到一个对策不比Beta更坏的。如果搜索过程中返回Beta或比Beta更好的值，那就够好的了，走棋的一方就没有机会使用这种策略了。 在搜索着法时，每个搜索过的着法都返回跟Alpha和Beta有关的值，它们之间的关系非常重要，或许意味着搜索可以停止并返回。 如果某个着法的结果小于或等于Alpha，那么它就是很差的着法，因此可以抛弃。因为我前面说过，在这个策略中，局面对走棋的一方来说是以Alpha为评价的。 如果某个着法的结果大于或等于Beta，那么整个结点就作废了，因为对手不希望走到这个局面，而它有别的着法可以避免到达这个局面。因此如果我们找到的评价大于或等于Beta，就证明了这个结点是不会发生的，因此剩下的合理着法没有必要再搜索。 如果某个着法的结果大于Alpha但小于Beta，那么这个着法就是走棋一方可以考虑走的，除非以后有所变化。因此Alpha会不断增加以反映新的情况。有时候可能一个合理着法也不超过Alpha，这在实战中是经常发生的，此时这种局面是不予考虑的，因此为了避免这样的局面，我们必须在博弈树的上一个层局面选择另外一个着法。 在第二个口袋里找到烂鱼就相当于超过了Beta，如果口袋里没有烂鱼，那么考虑六盒装流行唱片的口袋会比三明治的口袋好，这就相当于超过了Alpha(在上一层)。算法如下，醒目的部分是在最小-最大算法上改过的：
int AlphaBeta(int depth, int alpha, int beta) {
if (depth == 0) {
return Evaluate();
}
GenerateLegalMoves();
while (MovesLeft()) {
MakeNextMove();
val = -AlphaBeta(depth - 1, -beta, -alpha);
UnmakeMove();
if (val >= beta) {
return beta;
}
if (val > alpha) {
alpha = val;
}
}
return alpha;
}
把醒目的部分去掉，剩下的就是最小-最大函数。可以看出现在的算法没有太多的改变。 这个函数需要传递的参数有：需要搜索的深度，负无穷大即Alpha，以及正无穷大即Beta：
val = AlphaBeta(5, -INFINITY, INFINITY);
这样就完成了5层的搜索。我在写最小-最大函数时，用了一个诀窍来避免用了“Min”还用“Max”函数。在那个算法中，我从递归中返回时简单地对返回值取了负数。这样就使函数值在每一次递归中改变评价的角度，以反映双方棋手的交替着子，并且它们的目标是对立的。 在Alpha-Beta函数中我们做了同样的处理。唯一使算法感到复杂的是，Alpha和Beta是不断互换的。当函数递归时，Alpha和Beta不但取负数而且位置交换了，这就使得情况比口袋的例子复杂，但是可以证明它只是比最小-最大算法更好而已。 最终出现的情况是，在搜索树的很多地方，Beta是很容易超过的，因此很多工作都免去了。 可能的弱点 这个算法严重依赖于着法的寻找顺序。如果你总是先去搜索最坏的着法，那么Beta截断就不会发生，因此该算法就如同最小-最大一样，效率非常低。该算法最终会找遍整个博弈树，就像最小-最大算法一样。 如果程序总是能挑最好的着法来首先搜索，那么数学上有效分枝因子就接近于实际分枝因子的平方根。这是Alpha-Beta算法可能达到的最好的情况。 由于国际象棋的分枝因子在35左右，这就意味着Alpha-Beta算法能使国际象棋搜索树的分枝因子变成6。 这是很大的改进，在搜索结点数一样的情况下，可以使你的搜索深度达到原来的两倍。这就是为什么使用Alpha-Beta搜索时，着法顺序至关重要的原因。 原文：http://www.seanet.com/~brucemo/topics/alphabeta.htm 译者：象棋百科全书网 ([email protected]) 类型：全译
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
Alpha-Beta搜索
David Eppstein */文
* 加州爱尔文大学(UC Irvine)信息与计算机科学系
浅的裁剪 假设你用最小-最大搜索(前面讲到的)来搜索下面的树：
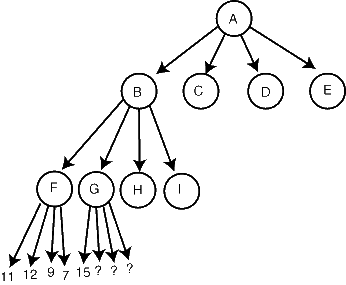你搜索到F，发现子结点的评价分别是11、12、7和9，在这层是棋手甲走，我们希望他选择最好的值，即12。所以，F的最小-最大值是12。 现在你开始搜索G，并且第一个子结点就返回15。一旦如此，你就知道G的值至少是15，可能更高(如果另一个子结点比G更好)。这就意味着我们不指望棋手乙走G这步了，因为就棋手乙看来，F的评价12要比G的15(或更高)好，因此我们知道G不在主要变例上。我们可以裁剪(Prune)结点G下面的其他子结点，而不要对它们作出评价，并且立即从G返回，因为对G作更好的评价只是浪费时间。 一般来说，像G一样只要有一个子结点返回比G的兄弟结点更好的值(对于结点G要走棋的一方而言)，就可以进行裁剪。 深的裁剪 我们来讨论更复杂的可能裁剪的情况。例如在同一棵搜索树中，我们评价的G、H和I都比12好，因此12就是结点B的评价。现在我们来搜索结点C，在下面两层我们找到了评价为10的结点N：
我们能用更为复杂的路线来作裁剪。我们知道N会返回10或更小(轮到棋手乙走棋，需要挑最小的)。我们不知道J能否返回10或更小，也不知道J的哪个子结点会更好。如果从J返回到C的是10或者更小的值，那么我们可以在结点C上作裁剪，因为它有更好的兄弟结点B。因此在这种情况下，继续找N的子结点就毫无意义。考虑其他情况，J的其他子结点返回比10更好的值，此时搜索N也是毫无意义的。所以我们只要看到10，就可以放心地从N返回。 Alpha-Beta的伪代码 一般来说，如果返回值比偶数层的兄弟结点好，我们就可以立即返回。如果我们在搜索过程中，把这些兄弟结点的最小值Beta作为参数来传递，我们就可以进行非常有效的裁剪。我们还用另一个参数Alpha来保存奇数层的结点。用这两个参数来进行裁剪是非常有效的，代码就写在下边。像上次一样，我们用负值最大(Negamax)的形式，即搜索树的层数改变时取负值。
double alphabeta(int depth, double alpha, double beta) {
if (depth <= 0 || 棋局结束) {
return evaluation();
}
就当前局面，生成并排序一系列着法;
for (每个着法 m) {
执行着法 m;
double val = -alphabeta(depth - 1, -beta, -alpha);
撤消着法 m;
if (val >= beta) {
return val;
}
if (val > alpha) {
alpha = val;
}
}
return alpha;
}
下次我们会解释为什么排序这一步是很重要的。 期望搜索 在根结点上我们如何为Alpha和Beta设定初值？ Alpha和Beta定义了一个评价的实数区间(Alpha, Beta)，这个区间是我们“感兴趣的”。如果某值比Beta大我们就会做裁剪并立即返回，因为我们知道它不是主要变例的一部分，我们对它的准确值不感兴趣，只需要知道它比Beta大。如果某值比Alpha小，我们不作裁剪，但是仍然对它不感兴趣，因为我们知道搜索树里肯定有一个着法会更好。 但是在搜索树的根结点，我们不知道感兴趣的评价是在哪个范围内，如果我们要保证不会因为意外而裁剪掉重要的部分，我们就设Alpha = -Infinity，Beta = Infinity(无穷大)。 但是，如果我们使用迭代加深，就可能有办法知道主要变例是怎么样的。假设我们猜其值为x(例如x就是前一次搜索到D -1深度时的值)，并设Epsilon为一个很小的值，它代表从D -1深度到D深度搜索评价的期望变化范围。我们可以尝试调用alphabeta(D, x - Epsilon, x + Epsilon)，那么可能发生三种情况： (1) 搜索的返回值会落在区间(x - Epsilon, x + Epsilon)内。这种情况下，我们知道它返回的是正确值，我们就能放心地选择这个着法，在搜索树中这个着法指向具有返回值的那个结点。 (2) 搜索会返回一个值v > x + Epsilon。这种情况下，我们知道搜索结果也至少是 x + Epsilon，但是我们不知道它到底是几(正确的主要变例可能被裁剪掉了，因为我们看到有别的着法的值大于Beta)。我们必须把我们所猜的值x调整得更高，然后再试一次(可能还要用更大的Epsilon)。这种情况称为“高出边界”(Fail High)。 (3) 搜索会返回一个值v < x - Epsilon。这种情况下，我们知道搜索结果也最多是 x + Epsilon，但是我们不知道它到底是几。我们必须把我们所猜的值x调整得更低，然后再试一次(可能还要用更大的Epsilon)。这种情况称为“低出边界”(Fail Low)。 即便有两种可能失败的情况，使用期望搜索(用一个比(-Infinity, Infinity)更小的区间(Alpha, Beta))总体来说效率会有所提高，因为它作了更多的裁剪。 分析 让我们对Alpha-Beta搜索作一下分析，来知道它为什么是个很有用的算法。跟普通的算法不同，我们采用“Beta情况的分析”，即假设任何可能的情况下都会发生Alpha-Beta裁剪。下一次我们会知道如何让Alpha-Beta搜索接近我们的所分析的情况。在这里我只考虑浅的裁剪，因为它会让分析变得更加简单。 在最好的情况下，除了主要变例上的结点不会裁剪外(如果这个结点也被裁剪了，那么整个算法会高出边界或低出边界，这当然不是最好的情况)，在裁剪前，深D -1层的每个结点只会搜索一个深D层的子结点。 但是在深D -2层时，谁也没有被裁剪，因为所有的子结点都返回大于或等于Beta的值，而D -2层是要取负数，因此它们都小于或等于Alpha。 继续朝树根走，D -3层的每个结点(除了主要变例外)都被裁剪，而D -4层谁也没被裁剪，等等。 因此，如果搜索树的分枝因子是B，那么在搜索树一半的深度上，结点以因子B作增长，而在另一半的深度上则保持不变(我们忽略了主要变例)。所以这个搜索树所有要搜索的结点数，粗略地写成BD/2 = sqrt(B)D。因此Alpha-Beta搜索最终可以将分枝因子减少为原来的平方根那么多，因此它可以让我们搜索原来两倍的深度。正因为这个原因，它是所有基于最小-最大策略的棋类对弈程序的最重要的算法。 【译注：原作者一开始提到的“浅的裁剪”和“深的裁剪”这两个概念，实际上包含了Alpha-Beta搜索的两个层次，前者只是用过传递参数Beta对搜索树作了部分裁剪，可以称为Beta搜索，而后者增加一个传递参数Alpha，使得裁剪更加充分，这就形成了Alpha-Beta搜索。 Beta搜索的伪代码是：
double alphabeta(int depth, double beta) {
if (depth <= 0 || 棋局结束) {
return evaluation();
}
就当前局面，生成并排序一系列着法;
double alpha = -infty;
for (每个着法 m) {
执行着法 m;
double val = -alphabeta(depth - 1, -alpha);
撤消着法 m;
if (val >= beta) {
return val;
}
if (val > alpha) {
alpha = val;
}
}
return alpha;
}
对红色部分加一些改进，就变成Alpha-Beta搜索的伪代码了。】 原文：http://www.ics.uci.edu/~eppstein/180a/970422.html 译者：象棋百科全书网 ([email protected])
类型：全译加译注
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
Alpha-Beta剪枝算法(Alpha Beta Pruning)
[说明] 本文基于<>，文中的图片均来源于此笔记。
Alpha-Beta剪枝用于裁剪搜索树中没有意义的不需要搜索的树枝，以提高运算速度。
假设α为下界，β为上界，对于α ≤ N ≤ β:
若 α ≤ β 则N有解。
若 α > β 则N无解。
下面通过一个例子来说明Alpha-Beta剪枝算法。
上图为整颗搜索树。这里使用极小极大算法配合Alpha-Beta剪枝算法，正方形为自己（A），圆为对手（B）。
初始设置α为负无穷大，β为正无穷大。
对于B(第四层)而已，尽量使得A获利最小，因此当遇到使得A获利更小的情况，则需要修改β。这里3小于正无穷大，所以β修改为3。
(第四层)这里17大于3，不用修改β。
对于A(第三层)而言，自己获利越大越好，因此遇到利益值大于α的时候，需要α进行修改，这里3大于负无穷大，所以α修改为3
B(第四层)拥有一个方案使得A获利只有2，α=3, β=2, α > β, 说明A(第三层)只要选择第二个方案, 则B必然可以使得A的获利少于A(第三层)的第一个方案,这样就不再需要考虑B(第四层)的其他候选方案了,因为A(第三层)根本不会选取第二个方案,多考虑也是浪费.
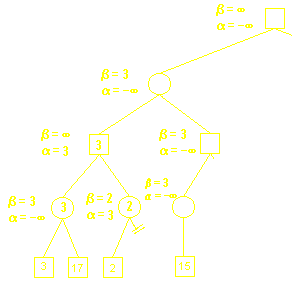
B(第二层)要使得A利益最小,则B(第二层)的第二个方案不能使得A的获利大于β, 也就是3. 但是若B(第二层)选择第二个方案, A(第三层)可以选择第一个方案使得A获利为15, α=15, β=3, α > β, 故不需要再考虑A(第三层)的第二个方案, 因为B(第二层)不会选择第二个方案.
A(第一层)使自己利益最大,也就是A(第一层)的第二个方案不能差于第一个方案, 但是A(第三层)的一个方案会导致利益为2, 小于3, 所以A(第三层)不会选择第一个方案, 因此B(第四层)也不用考虑第二个方案.
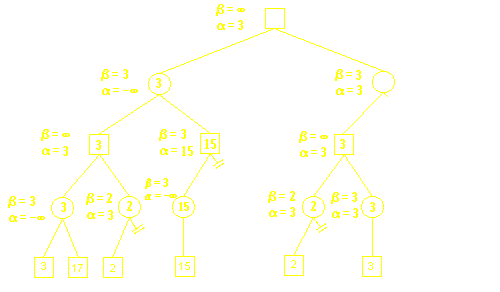
当A(第三层)考虑第二个方案时,发现获得利益为3,和A(第一层)使用第一个方案利益一样.如果根据上面的分析A(第一层)优先选择了第一个方案,那么B不再需要考虑第二种方案,如果A(第一层)还想进一步评估两个方案的优劣的话, B(第二层)则还需要考虑第二个方案,若B(第二层)的第二个方案使得A获利小于3,则A(第一层)只能选择第一个方案,若B(第二层)的第二个方案使得A获利大于3,则A(第一层)还需要根据其他因素来考虑最终选取哪种方案.
