2022年第十三届蓝桥杯大赛C/C++语言B组省赛题解

首先说明：以下题解为本人当时参赛时的解答，请自行检查运行结果的正误
废话不多说，直接上题

试题A：九进制转十进制

这题没说的，直接简单的“鸭皮”

十进制：2022=2×10³+0×10²+2×10¹+2同样得到：
九进制：2×9³+0×9²+2×9¹+2×9⁰=（结果）

试题B：顺子日期

这题出的有点问题，题目中说的123算顺子，但是0到底包不包括在内，题目也没有给出解答，所以，这题如果算0就是14，不算0就是4，最后好像都给算对了。还是有争议的一道题。当时我也没有考虑0，就直接写了个4
答案：4||14

试题C：刷题统计

这题也没什么好说的，只要给定足够的空间就能拿满分，如果没有考虑到也没关系，部分数据还是能通过，可以拿到一点分数的（比如我……）请自觉将下述代码中的int换成long long

#include 
int main()
{
	int a=0,b=0,n=0,day=0,sum=0;
	scanf("%d%d%d",&a,&b,&n);
	
	while(n){
		day++;
		if(day%6==0||day%7==0){
			sum+=b;
		}
		else{
			sum+=a;
		}
		if(sum>=n){
			break;
		}	
	}
	printf("%d",day);
	return 0;
}

试题D：修剪灌木

这个题虽然说从左到右修建，但是她修建完一圈，从右向左时一样的道理，而树木白天到晚上还会长高，所以用加减法来实现上述问题。晚上做减法，白天长高做加法。再分别讨论是奇数和偶数两种情况，将每次循环的最大值记录下来就可以了。

#include 
#define N 10000
int main()
{
	int x=0,a[N]={0,0,0,0,0,0,0,0,0,0},i,j,k,h,sum=0;
	scanf("%d",&x);
	int b[N]={}; 
	
	for(h=1;h<10;h++){    //外层循环10次 
	
	if(h%2==0){  //超出范围 
			for(j=x-1;j>=0;j--){
				for(i=0;i<x;i++)
		a[i]++;           //实现白天加法 
	    
	    for(k=0;k<x;k++)
	    	if(a[k]>b[k])
	    		b[k]=a[k];
	    		
	    a[j]=0;      //夜晚减法
		
	}				 
	}

//******************************************************************	
	else if(h%2!=0){
		for(j=0;j<x;j++){
		    for(i=0;i<x;i++)
		        a[i]++;           //实现白天加法 
		
		for(k=0;k<x;k++)
	    	if(a[k]>b[k])
	    	   b[k]=a[k];
	    	   
	    a[j]=0;      //夜晚减法 	 
	}
	
	}
}

	for(i=0;i<x;i++)
		printf("%d\n",b[i]-1);      //输出最大值 

	return 0;
	 
}

试题E：X进制减法

最经典的海伦-秦九韶算法，具体的算法和思想注释在了代码里，能看懂的同学最好了，看不懂没关系，这个题目稍微有点难度。

#include
#include
#include
using namespace std;
 
typedef long long LL;
 
LL mod=1000000007;
int n,a,b;
int an[100010],bn[100010];
 
int main()
{
	cin>>n;
	cin>>a;
	for(int i=a;i>=1;i--) cin>>an[i];//这里我们需要的是低位对齐进行减法，高位不用管 
	cin>>b;
	for(int i=b;i>=1;i--) cin>>bn[i];//依然是从低位在0处 
	
	LL ans=0;
	for(int i=a;i>=1;i--)//这里不需要取a与b的最高位啊，因为a是严格大于b的，如果位数a
	{                    //所以a的长度只能大于等于b 
		ans=(ans*max({2,an[i]+1,bn[i]+1})+an[i]-bn[i])%mod//秦九韶算法，这里算的是差值，所以要加上an[i]-bn[i] 
	}//ans({})这样可以计算多个数的最大值，我们最低为2，最高为最大值加一 
	cout<<ans<<endl;//直接输出即可； 
	
}

试题F：统计子矩阵

这个题我在考试时候也是最后做出来的，只要思路能清晰，这道题运用普通的暴力求解是可以做出来的。

#include 
int main()
{
	int n,m,i,k,j,r,h,c,b,sum=0,ans=0;
	scanf("%d%d%d",&n,&m,&k);
	
	int a[n][m];
	
	for(i=0;i<n;i++){
		for(j=0;j<m;j++){
			scanf("%d",&a[i][j]);   //输入 
		}
	}
	
	for(i=1;i<=n;i++){   //行       
		for(j=1;j<=m;j++){   //纵    //定义行和列 
		
			for(r=0;r<n;r++){ 
				for(h=0;h<m;h++){   //遍历 
					
					if(r+i<=n&&j+h<=m){
						sum=0;
						for(c=r;c<r+i;c++){
							for(b=h;b<h+j;b++){
								sum+=a[c][b];     //求和 
					
							}
						}
						if(sum<=k) ans++;
					}
					
				}
			}
		}
	}
	
	printf("%d",ans);
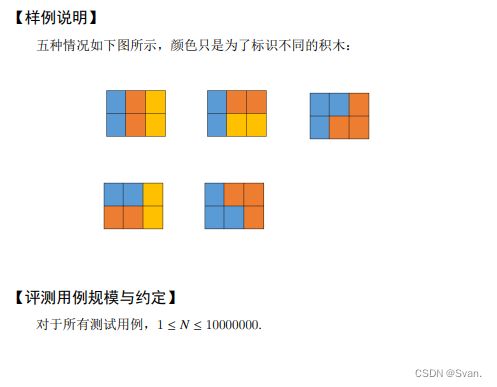
	return 0; 
}

试题G：积木画

此题目是洛谷的类似题目（覆盖墙面），不是很简单。

#include
#include
#include
#include
using namespace std;
int n;
int mod=1000000007;
int f[1000010][2];
int main(){
    scanf("%d",&n);
    f[0][0]=1;f[1][0]=1;
    for(int i=2;i<=n;i++){
        f[i][0]=(f[i-1][1]+f[i-1][0]+f[i-2][0])%mod;
        f[i][1]=(f[i-1][1]+2*f[i-2][0])%mod;
    }
    cout<<f[n][0];
}

至此，如果上述题目你都做的差不多，省一是稳了
下面的题目就供大家自行学习了，本人在考试时候也做的很垃圾。

这题我没做出来！！！！

这题的数据应该只能跑起来一部分……

#include 

using namespace std;

long long cnt=0;

int mod=1000000007;

int  n,m,c=2;

void dfs(int x,int y,int c){
	if(x<0||y<0) return ;
	if(x==0&&y==1&&c==1){
		cnt++;
		cnt=cnt%mod;
		return;
	}
	if(x>0) dfs(x-1,y,c*2);
	if(y>0) dfs(x,y-1,c-1);
}

int main(){
	int m,n;
	cin>>n>>m;
	dfs(n,m,c);
	cout<<cnt<<endl;
}

#include
#include
#include
#include
using namespace std;
 
typedef long long LL;
const int M=200010,N=10;
LL arr[M][N];
int main()
{
	int n;
	cin>>n;
	
	LL sta[10],top=0,mx=0,cnt=0;
	for(int i=0;i<n;i++)
	{
		top=0;
		LL p;
		cin>>p;
		while(p>1) sta[top++]=p,p=sqrt(p/2+1);//把这个数分解存储 
		mx=max(mx,top);//我们要找到最高的那个位置 
		cnt+=top;//一次剪一下，最大修剪次数 
		for(int j=0,k=top-1;k>=0;j++,k--)
		    arr[i][j]=sta[k];//把数的分解结果逆序存储进去 
	}
	for(int i=0;i<mx;i++)
	{
		for(int j=1;j<n;j++)
		{
			if(arr[j][i]==arr[j-1][i]&&arr[j-1][i])//只要他和前面相同，代表可以一起修剪，最大修建次数减减 
			cnt--;
		}
	}
	cout<<cnt<<endl;//直接输出结果即可 
 } 

省赛考完我直接睡了一下午，冷的一批。希望正在准备2023年蓝桥杯的你一定要加油努力，是金子总会发光的！！！！！