（深度学习快速入门）第三章第三节1：深度学习必备组件之数据集处理和参数初始化

从前文中可以看出，一个深度学习项目涉及“组件”非常多，例如损失函数、优化器、数据集处理等等，这些都需要我们去仔细研究，所以本节对这些深度学习中的重要组件进行详细叙述

一：数据集的处理

（1）数据集划分

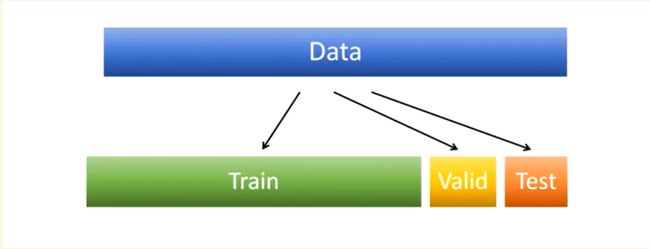
数据集划分：对于一个数据集，我们一般会将其划分为如下三个部分

• Train_set（训练集）：占用70%，用于训练模型
• Val_set（验证集）：占用20%，用于验证模型性能，并以此调节参数、选择最佳模型
• Test_set（测试集）：占用10%，用于检验模型是否能够很好的预测输出，是否具有泛化能力

在划分数据集时注意

• 这三个子集尽量保持同分布（随机）
• 三个子集内的数据绝对不能重合，或者说污染
• 在数据量较少，验证集和测试集可以合并为测试集，此时七三分即可

之所以需要验证集是因为

（2）数据集验证

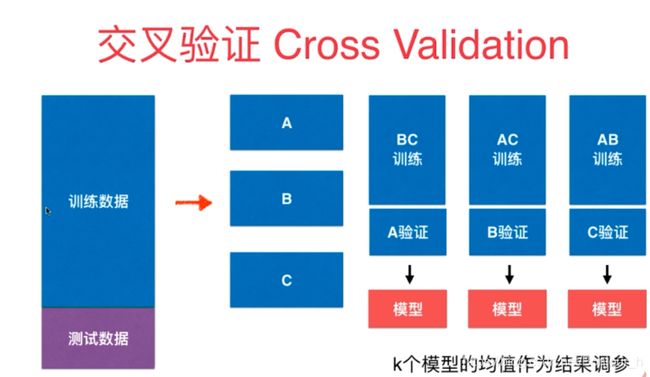
因此，我们的模型不能通过测试集来评判，这样做反而会使模型过拟合测试数据，其参数只会针对测试数据有效，所以模型的验证应该要在验证集上。对于数据集的验证我们最常用的方法便是k-折交叉验证，它是指随机地将数据集切分为 k 个互不相交的大小相同的子集，然后将 k-1 个子集当成训练集训练模型，剩下的一个子集当测试集测试模型；将上一步对可能的 k 种选择重复进行 (每次挑一个不同的子集做测试集)；这样就训练了 k 个模型，每个模型都在相应的测试集上计算测试误差，得到了 k 个测试误差，对这 k 次的测试误差取平均便得到一个交叉验证误差

如下图，k=3时就称之为3折交叉验证

（3）标准化和归一化

归一化（Standardization）：将数据映射到[0, 1]或[-1, 1]之间，以此消除量纲

$$\frac{x_i-min(x_i)}{max(x_i)-min(x_i)}$$

标准化(Normalization)：将数据变换为均值为0，标准差为1的分布

$$\frac{x_i-u}{\sigma }$$

二：模型参数的初始化

（1）梯度消失和梯度爆炸

反向传播算法本质就是链式法则，而链式法则是一个连乘的形式，当层数越深的时候，梯度将以指数形式传播，所以梯度消失和梯度爆炸就是随着网络层数的增加，而最终使梯度值为接近0或非常大，继而无法继续训练的现象

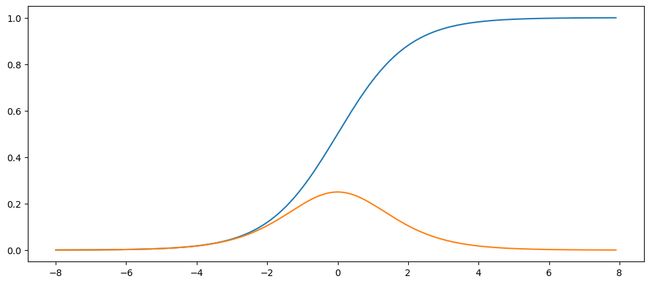
梯度消失：sigmoid函数在早期是非常流行的，因为早期的人工神经网络受到生物神经网络的启发，神经元要么完全激活要么完全不激活（就像生物神经元）的想法很有吸引力。然而，它却是导致梯度消失问题的⼀个常见的原因。如下图当sigmoid函数输入过小或过大时梯度都会消失

import torch
from matplotlib import pyplot as plt

x = torch.arange(-8.0, 8.0, 0.1, requires_grad=True)
y = torch.sigmoid(x)
y.backward(torch.ones_like(x))
plt.figure(figsize=(12, 5))
plt.plot(x.detach(), y.detach())
plt.plot(x.detach(), x.grad.numpy())

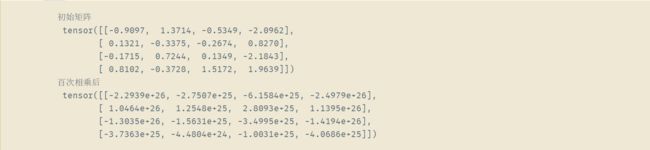
梯度爆炸：梯度爆炸往往可能是由于不良初始化导致，没有机会让优化器收敛。如下图，生成100个高斯随机矩阵，并将它们与某个初始矩阵相乘，由于我们选择的尺度（${\sigma }^2=1$），导致矩阵乘积发生爆炸

M = torch.normal(0, 1, size=(4, 4))
print("初始矩阵\n", M)
for i in range(100):
    M = torch.mm(M, torch.normal(0, 1, size=(4, 4)))
print("百次相乘后\n", M)

（2）模型参数初始化方法

①：Xavier初始化

Xavier初始化：基本思想是为了使得网络中信息更好的流动，每一层输出的方差应该尽量相等，Xavier初始化的实现就是下面的均匀分布

$$w\sim U(-a,a)$$

其中$a=gain\ast \sqrt{\frac{6}{fa{n}_{in}+fa{n}_{out}}}$，$gain$是指争议，可以通过不同的激活函数算出

②：Kaiming方法

Kaiming方法：ReLU激活函数属于非饱和类激活函数，并不会出现类似Sigmoid和tanh激活函数使用过程中可能存在的梯度消失或梯度爆炸问题，反而因为ReLU激活函数的不饱和特性，ReLU激活函数的叠加极有可能出现神经元活性消失的问题，很明显，该类问题无法通过Xavier初始化解决。目前通用的针对ReLU激活函数的初始化参数方法，是由何凯明所提出的HE初始化方法，也被称为Kaiming方法

$$w\sim U(-bound,bound)$$

其中$bound=gain\ast \sqrt{\frac{6}{(1+a^2)+fanin}}$，$a$是激活函数leaky_relu的负半轴斜率

---

from torch import nn
model = nn.Linear(in_features=16, out_features=128)
print("Xavier方法")
print(model.weight)
nn.init.xavier_uniform_(model.weight, gain=nn.init.calculate_gain('tanh'))
print(model.weight)
print("Kaiming方法")
nn.init.kaiming_uniform_(model.weight, a=1, mode='fan_in', nonlinearity='leaky_relu')
print(model.weight)