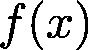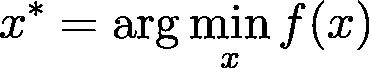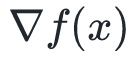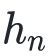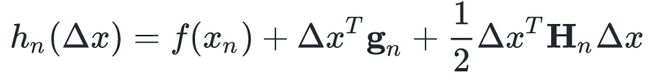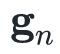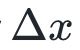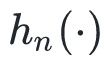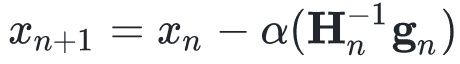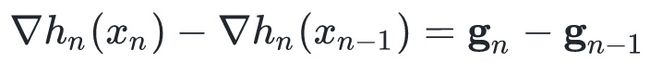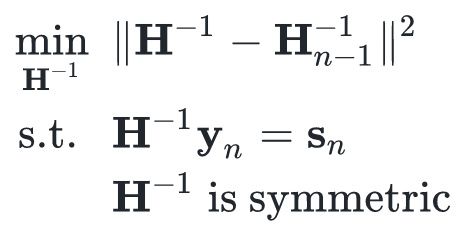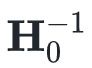l bfgs算法java代码_数值优化：理解L-BFGS算法

译自《Numerical Optimization: Understanding L-BFGS》，本来只想作为学习CRF的补充材料，读完后发现收获很多，把许多以前零散的知识点都串起来了。对我而言，的确比零散地看论文要轻松得多。原文并没有太多关注实现，对实现感兴趣的话推荐原作者的golang实现。

数值优化是许多机器学习算法的核心。一旦你确定用什么模型，并且准备好了数据集，剩下的工作就是训练了。估计模型的参数(训练模型)通常归结为最小化一个多元函数

，其中输入

是一个高维向量，也就是模型参数。换句话说，如果你求解出：

那么

*就是最佳的模型参数(当然跟你选择了什么目标函数有关系)。

在这篇文章中，我将重点放在讲解L-BFGS算法的无约束最小化上，该算法在一些能用上批处理优化的ML问题中特别受欢迎。对于更大的数据集，则常用SGD方法，因为SGD只需要很少的迭代次数就能达到收敛。在以后的文章中，我可能会涉及这些技术，包括我个人最喜欢的AdaDelta 。

注 ： 在整个文章中，我会假设你记得多元微积分。所以，如果你不记得什么是梯度或海森矩阵，你得先复习一下。

牛顿法

大多数数值优化算法都是迭代式的，它们产生一个序列，该序列最终收敛于

，使得

达到全局最小化。假设，我们有一个估计

，我们希望我们的下一个估计

有这种属性：

。

牛顿的方法是在点

附近使用二次函数近似

。假设

是二次可微的，我们可以用

在点

的泰勒展开来近似

。

其中，

和

分别为目标函数

在点

处的梯度和Hessian矩阵。当

时，上面的近似展开式是成立的。你可能记得微积分中一维泰勒多项式展开，这是其推广。

为了简化符号，将上述二次近似记为

，我们把生成

这样的二次近似的迭代算法中的一些概念简记如下：

不失一般性，我们可以记

，那么上式可以写作：

其中

和

分别表示目标函数在点

处的梯度和Hessian矩阵。

我们想找一个

，使得

在

的二次近似最小。上式对

求导：

任何使得

的

都是

的局部极值点，如果我们假设

是凸函数，则

是正定的，那么局部极值点就是全局极值点(凸二次规划)。

解出

：

这就得到了一个很好的搜索方向，在实际应用中，我们一般选择一个步长α，即按照下式更新

：

使得

相比

的减小量最大化。

迭代算法伪码：

步长α的确定可以采用任何line search算法，其中最简单的一种是backtracking line search。该算法简单地选取越来越小的步长α，直到

的值小到满意为止。关于line search算法的详情请参考

Line Search Methods.pdf或

Lecture 5- Gradient Descent.pdf。

在软件工程上，我们可以将牛顿法视作实现了下列Java接口的一个黑盒子：

public interface TwiceDifferentiableFunction

{

// compute f(x)

double valueAt(double[] x);

// compute grad f(x)

double[] gradientAt(double[] x);

// compute inverse hessian H^-1

double[][] inverseHessian(double[] x);

}

如果你有兴趣，你还可以通过一些枯燥无味的数学公式，证明对任意一个凸函数，上述算法一定可以收敛到一个唯一的最小值

，且不受初值

的影响。对于非凸函数，上述算法仍然有效，但只能保证收敛到一个局部极小值。在上述算法于非凸函数的实际应用中，用户需要注意初值的选取以及其他算法细节。

巨大的海森矩阵

牛顿法最大的问题在于我们必须计算海森矩阵的逆。注意在机器学习应用中，

的输入的维度常常与模型参数对应。十万维度的参数并不少见(SVM中文文本分类取词做特征的话，就在十万这个量级)，在一些图像识别的场景中，参数可能上十亿。所以，计算海森矩阵或其逆并不现实。对许多函数而言，海森矩阵可能根本无法计算，更不用说表示出来求逆了。

所以，在实际应用中牛顿法很少用于大型的优化问题。但幸运的是，即便我们不求出

在

的精确

，而使用一个近似的替代值，上述算法依然有效。

拟牛顿法

如果不求解

在

的精确

，我们要使用什么样的近似呢？我们使用一种叫QuasiUpdate的策略来生成

的近似，先不管QuasiUpdate具体是怎么做的，有了这个策略，牛顿法进化为如下的拟牛顿法：

跟牛顿法相比，只是把

的计算交给了QuasiUpdate。为了辅助QuasiUpdate，计算了几个中间变量。QuasiUpdate只需要上个迭代的

、输入和梯度的变化量(

和

)。如果QuasiUpdate能够返回精确的

的逆，则拟牛顿法等价于牛顿法。

在软件工程上，我们又可以写一个黑盒子接口，该接口不再需要计算海森矩阵的逆，只需要在内部更新它，再提供一个矩阵乘法的接口即可。事实上，内部如何处理，外部根本无需关心。用Java表示如下：

public interface DifferentiableFunction

{

// compute f(x)

double valueAt(double[] x);

// compute grad f(x)

double[] gradientAt(double[] x);

}

public interface QuasiNewtonApproximation

{

// update the H^{-1} estimate (using x_{n+1}-x_n and grad_{n+1}-grad_n)

void update(double[] deltaX, double[] deltaGrad);

// H^{-1} (direction) using the current H^{-1} estimate

double[] inverseHessianMultiply(double[] direction);

}

注意我们唯一用到海森矩阵的逆的地方就是求它与梯度的乘积，所以我们根本不需要在内存中将其显式地、完全地表示出来。这对接下来要阐述的L-BFGS特别有用。如果你对实现细节感兴趣，可以看看作者的golang实现。

近似海森矩阵

QuasiUpdate到底要如何近似海森矩阵呢？如果我们让QuasiUpdate忽略输入参数，直接返回单位矩阵，那么拟牛顿法就退化成了梯度下降法了，因为函数减小的方向永远是梯度

。梯度下降法依然能保证凸函数

收敛到全局最优对应的

，但直觉告诉我们，梯度下降法没有利用到

的二阶导数信息，收敛速度肯定更慢了。

我们先把

的二次近似写在下面，从这里找些灵感。

Secant Condition

的一个性质是，它的梯度与

在

处的梯度一致(近似函数的梯度与原函数的梯度一致，这才叫近似嘛)。也就是说我们希望保证：

我们做个减法：

由中值定理，我们有：

这个式子就是所谓的Secant Condition，该条件保证

至少对

而言是近似海森矩阵的。

等式两边同时乘以

，并且由于我们定义过：

于是我们得到：

对称性

由定义知海森矩阵是函数的二阶偏导数矩阵，即

，所以海森矩阵一定是对称的。

BFGS更新

形式化地讲，我们希望

至少满足上述两个条件：

对

和

而言满足Secant Condition

满足对称性

给定上述两个条件，我们还希望

相较于

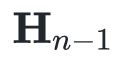的变化量最小。这类似“ MIRA 更新”，我们有许多满足条件的选项，但我们只选那个变化最小的。这种约束形式化地表述如下：

式中

。我不知道如何推导它，推导的话需要用很多符号，并且费时费力。

这种更新算法就是著名的Broyden–Fletcher–Goldfarb–Shanno (BFGS)算法，该算法是取发明者名字的首字母命名的。

关于BFGS，有一些需要注意的点：

只要

是正定的，

就一定是正定的。所以我们只需要选择一个正定的

即可，甚至可以选择单位矩阵。

和

还存在简单的算术关系，给定

和

和

，我们就能倒推出

。

把这些知识放到一起，我们就得出了BFGS更新的算法，给定方向d，该算法可以计算出

，却不需要求

矩阵，只需要按照上述表达式不断地递推即可：

由于

的唯一作用就是计算

，我们只需用该更新算法就能实现拟牛顿法。

L-BFGS：省内存的BFGS

BFGS拟牛顿近似算法虽然免去了计算海森矩阵的烦恼，但是我们仍然需要保存每次迭代的

和

的历史值。这依然没有减轻内存负担，要知道我们选用拟牛顿法的初衷就是减小内存占用。

L-BFGS是limited BFGS的缩写，简单地只使用最近的m个

和

记录值。也就是只储存

和

，用它们去近似计算

。初值

依然可以选取任意对称的正定矩阵。

L-BFGS改进算法

在实际应用中有许多L-BFGS的改进算法。对不可微分的函数，可以用othant-wise 的L-BFGS改进算法来训练

正则损失函数。

不在大型数据集上使用L-BFGS的原因之一是，在线算法可能收敛得更快。这里甚至有一个L-BFGS的在线学习算法，但据我所知，在大型数据集上它们都不如一些SGD的改进算法(包括 AdaGrad 或 AdaDelta)的表现好。

Reference