【阅读笔记】低照度图像增强-《Fast efficient algorithm for enhancement of low lighting video》
本文介绍的是一种比较实用的低照度图像增强效果很好的方法,Xuan Dong论文《Fast efficient algorithm for enhancement of low lighting video》
概述
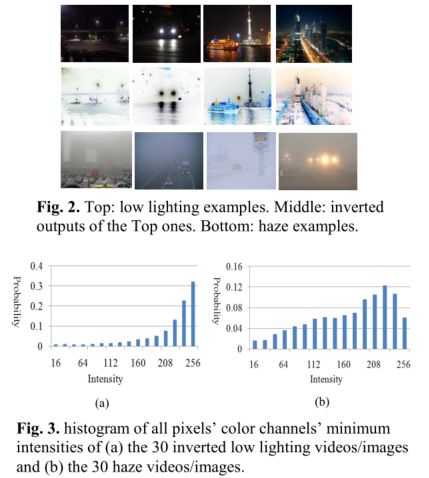
低光照图像取反(255 - 低光照图像),和有雾图像存在一些共性,比如在天空或者遥远的背景这些地方,亮度值都是很高的,但在近景的 RGB 三通道中至少有一个亮度值很低。作者提出直接用去雾算法对低光照图像的反转图像处理,去雾结果再取反得到低照度增强结果。
低照度图像增强算法
大气散射模型
大多透雾算法基于大气散射模型,模型如下:
I ( x ) = J ( x ) t ( x ) + A ( 1 − t ( x ) ) I (x) = J (x)t(x) + A(1 − t(x)) I(x)=J(x)t(x)+A(1−t(x))
其中, I ( x ) I(x) I(x)表示含雾图, J ( x ) J(x) J(x)表示无雾图, A A A表示大气光模型, t ( x ) = e − β d ( x ) t(x)=e^{- \beta d(x)} t(x)=e−βd(x)表示传输率矩阵, β \beta β 表示大气散射系数, d ( x ) d(x) d(x)表示图像区域的景深。雾越浓,到达相机的物体反射的光越少,即传输率越小。
上式可以改写为:
J ( x ) = I ( x ) − A t ( x ) + A J (x) = \frac{I (x) - A}{t(x)}+A J(x)=t(x)I(x)−A+A
为了得到 J ( x ) J(x) J(x),重点在估计 A A A和 t ( x ) t(x) t(x)。
暗通道先验知识:
在大部分无雾图像的无天空区域,像素中至少存在一个颜色通道存在很低非常低的亮度值。这个最低的亮度值几乎等同于0。因此,对于一个观测图像J,其暗通道趋近于0,即
J d a r k ( X ) = m i n y ∈ Ω ( x ) ( m i n c ∈ r , g , b J c ( y ) ) → 0 J^{dark}(X) = min_{y \in \Omega (x)}(min_{c \in {r,g,b }} J^{c}(y)) \to 0 Jdark(X)=miny∈Ω(x)(minc∈r,g,bJc(y))→0
其中, J c J^{c} Jc表示彩色图像每个通道, Ω ( x ) \Omega(x) Ω(x)表示以 x x x为中心的窗口
透雾算法
基于大气散射模型,透雾模型的方法步骤如下:
1、从雾图I (x) 估计传输率矩阵t(x)
2、估计大气光值A
3、通过公式估计无雾图J(x)
首先求出每个像素RGB分量中的最小值,存入一副和原始图像大小相同的灰度图中,然后再对这幅灰度图进行最小值滤波,滤波的半径由窗口大小决定,一般有 W i n d o w S i z e = 2 ∗ R a d i u s + 1 WindowSize = 2 * Radius + 1 WindowSize=2∗Radius+1
将雾模型
I ( x ) = J ( x ) t ( x ) + A ( 1 − t ( x ) ) I (x) = J (x)t(x) + A(1 − t(x)) I(x)=J(x)t(x)+A(1−t(x))
处理为:
I c ( x ) A c = J c ( x ) A c t ( x ) + 1 − t ( x ) \frac{I^{c} (x)}{A^{c}} = \frac{J^{c} (x)}{A^{c}}t(x) + 1 − t(x) AcIc(x)=AcJc(x)t(x)+1−t(x)
假设在窗口内透射率$ t(x) 为常数,定义为 为常数,定义为 为常数,定义为\tilde t(x) , , ,A$值已知。对上式求两次最小值运算,得到
m i n y ∈ Ω ( x ) ( m i n c I c ( y ) A c ) = t ~ ( x ) m i n y ∈ Ω ( x ) ( m i n c J c ( y ) A c ) + 1 − t ~ ( x ) \underset {y \in \Omega (x)}{min}(\underset{c}{min} \frac{I^{c} (y)}{A^{c}}) = \tilde t(x) \underset {y \in \Omega (x)}{min}(\underset{c}{min} \frac{J^{c} (y)}{A^{c}})+ 1 − \tilde t(x) y∈Ω(x)min(cminAcIc(y))=t~(x)y∈Ω(x)min(cminAcJc(y))+1−t~(x)
根据暗原色先验理论
J d a r k ( x ) = m i n y ∈ Ω ( x ) ( m i n c J c ( y ) ) = 0 J^{dark}(x) = \underset {y \in \Omega (x)}{min}(\underset{c }{min} J^{c}(y)) = 0 Jdark(x)=y∈Ω(x)min(cminJc(y))=0
推导出
m i n y ∈ Ω ( x ) ( m i n c J c ( y ) A c ) = 0 \underset {y \in \Omega (x)}{min}(\underset{c }{min} \frac{J^{c}(y)}{A^{c}}) = 0 y∈Ω(x)min(cminAcJc(y))=0
带入透射率为常数的公式,得到透射率预估值
t ~ ( x ) = 1 − m i n y ∈ Ω ( x ) ( m i n c I c ( y ) A c ) \tilde t(x) = 1-\underset {y \in \Omega (x)}{min}(\underset{c }{min} \frac{I^{c}(y)}{A^{c}}) t~(x)=1−y∈Ω(x)min(cminAcIc(y))
上式添加一个限制系数,得到 t ~ ( x ) \tilde t(x) t~(x):
t ~ ( x ) = 1 − ω m i n y ∈ Ω ( x ) ( m i n c I c ( y ) A c ) \tilde t(x) = 1-\omega\underset {y \in \Omega (x)}{min}(\underset{c }{min} \frac{I^{c}(y)}{A^{c}}) t~(x)=1−ωy∈Ω(x)min(cminAcIc(y))
ω \omega ω取值0.95
以上假设全球达气光A值时已知的,在实际中,我们可以借助于暗通道图来从有雾图像中获取该值。具体步骤如下:
1)从暗通道图中按照亮度的大小取前0.1%的像素。
2)在这些位置中,在原始有雾图像I中寻找对应的具有最高亮度的点的值,作为 A A A值。
算法参数优化
文中自适应调节 t ( x ) t(x) t(x),如下式
t ′ ( x ) = { 2 ∗ t ( x ) , 0 < t ( x ) < 0.5 1 , 0.5 < t ( x ) < 1 t'(x) = \begin{cases} 2*t(x),0
优化 t ( x ) t(x) t(x)如下,增强暗区提亮,亮区微处理,效果更好
t ′ ( x ) = { t ( x ) 2 ∗ 2 , 0 < t ( x ) < 0.5 t ( x ) , 0.5 < t ( x ) < 1 t'(x) = \begin{cases} t(x)^2*2,0
效果对比









算法实现参考
https://github.com/AomanHao/ISP_Low_Light_Image_Enhancement