数字图像处理(第三版,Rafeal C. Gonzalez, Richard E. Woods)--灰度变换与空间滤波
它的与众不同之处在于,是透过光线看阴影还是透过阴影看亮度。 ----大卫·林赛
- 灰度变换(映射)
-
- 直方图均衡(直方图线性变换)
- 直方图匹配(规定化)
- 局部直方图处理
- 空间滤波
-
- 平滑空间滤波器
- 锐化空间滤波器
- 混合空间增强法
- 模糊技术的应用
本章是在工作域的空间域技术 g ( x , y ) = T [ f ( x , y ) ] g(x,y)=T[f(x,y)] g(x,y)=T[f(x,y)]
图像增强使处理的图像比原图更适合特定的应用
空间滤波器(空间掩膜,核,模板,窗口) = 邻域 + 预定义操作
邻域size=[1,1]时称 点处理技术
灰度变换(映射)
| 变换 | 原理 | 功能 |
|---|---|---|
| 图像反转 | s = L − 1 − r s=L-1-r s=L−1−r | 视觉上增强细节 |
| 对数变换 | s = c log ( 1 + r ) s=c\log{(1+r)} s=clog(1+r) | 扩展暗像素对比度 |
| 指数(反对数变换) | c ( 2 r − 1 ) c(2^r-1) c(2r−1) | 扩展亮像素 |
| 幂律(伽马)变换 | s = c r γ s=cr^\gamma s=crγ | 显示设备校正,对比度增强 |
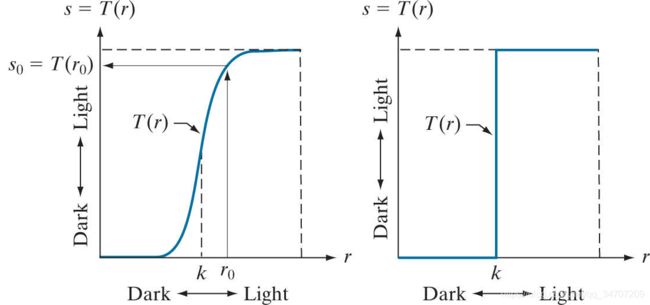
| 分段线性变换(对比度拉伸) | 上右图 | 扩展图像灰度级动态范围 |
| 分段线性变换(灰度级分层) | 增强AOI特征 | |
| 分段线性变换(比特平面分层) | 高阶比特面包含主要数据 输出{0,1}二值图像 |
压缩图片 |
直方图均衡(直方图线性变换)
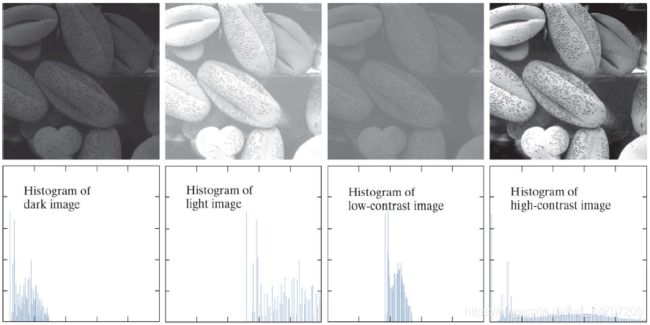
高对比度=灰度级宽+均匀分布 ⇒ 对比度拉伸
灰度映射 s = T ( r ) s=T(r) s=T(r):
(a) T ( r ) 在 [ 0 , L − 1 ] 上 单 调 递 增 T(r)在[0,L-1]上单调递增 T(r)在[0,L−1]上单调递增
(b) T ( r ) ∈ [ 0 , L − 1 ] T(r)\in[0,L-1] T(r)∈[0,L−1]
反映射 r = T − 1 ( s ) r=T^{-1}(s) r=T−1(s):
(a) ⇒ (a’) T ( r ) T(r) T(r)在 [ 0 , L − 1 ] [0,L-1] [0,L−1]上严格单调递增(保证一一映射)
∫ 0 s p s ( s ) d s = ∫ 0 r p s ( T ( r ) ) d T ( r ) d r d r = ∫ 0 r p r ( r ) d r \int_0^{s}p_s(s)ds=\int_0^{r}p_s(T(r))\frac{dT(r)}{dr}dr=\int_0^r p_r(r)dr ∫0sps(s)ds=∫0rps(T(r))drdT(r)dr=∫0rpr(r)dr 同 时 对 r 求 导 得 p s ( s ) ⇓ 同时对r求导得 p_s(s)\Downarrow 同时对r求导得ps(s)⇓ p s ( s ) = p r ( r ) d r d s \color{red}p_s(s)=p_r(r)\frac{dr}{ds} ps(s)=pr(r)dsdr 几何意义:ds对应的dr越大, p s ( s ) p_s(s) ps(s)就越大,大小由变换函数决定
eg:积累分布函数(CDF,comulative distribution function), p r ( r ) p_r(r) pr(r)的区间积分面积不变, p r ( r ) p_r(r) pr(r)越大 T ( r ) T(r) T(r)拉的越开,自动化均衡 s = T ( r ) = ( L − 1 ) ∫ 0 r p r ( w ) d w = 离 散 化 ⇒ s k = L − 1 M N ∑ j = 0 k n j p s ( s ) = p r ( r ) ∣ d r d s ∣ = p r ( r ) [ d T ( r ) d r ] − 1 = 1 L − 1 s=T(r)=(L-1)\int_0^rp_r(w)dw=离散化\Rightarrow s_k=\frac{L-1}{MN}\sum^k\limits_{j=0}n_j\\ p_s(s)=p_r(r)\begin{vmatrix}\frac{dr}{ds}\end{vmatrix}=p_r(r)[\frac{dT(r)}{dr}]^{-1}=\frac{1}{L-1} s=T(r)=(L−1)∫0rpr(w)dw=离散化⇒sk=MNL−1j=0∑knjps(s)=pr(r)∣∣dsdr∣∣=pr(r)[drdT(r)]−1=L−11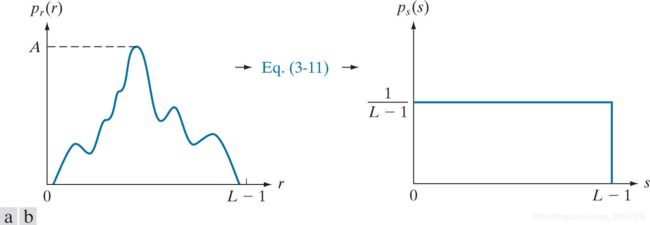
直方图匹配(规定化)
产生具有定形状的直方图进行增强
1.均衡输入图像 : s = T ( r ) = ( L − 1 ) ∫ 0 r p r ( w ) d w s=T(r)=(L-1)\int_0^rp_r(w)dw s=T(r)=(L−1)∫0rpr(w)dw
2.均衡输出图像 : z = G ( r ) = ( L − 1 ) ∫ 0 z p z ( t ) d t z=G(r)=(L-1)\int_0^zp_z(t)dt z=G(r)=(L−1)∫0zpz(t)dt 离散情况下建立映射表
3.均衡结果相等: G ( z ) = T ( r ) G(z)=T(r) G(z)=T(r) 离散情况下建立映射表
4.反变换映射: z = G − 1 ( s ) z=G^{-1}(s) z=G−1(s) 离散情况下查映射表, G − 1 ( s ) G^{-1}(s) G−1(s)有多个z时取最小的z(更亮)
离散化时只能得到近似结果,但大大简化了求解过程
G − 1 G^{-1} G−1意味着 G ( z ) G(z) G(z)必须严格单调, p z ( z i ) p_z(z_i) pz(zi)不能为0,在离散情况下查映射表可以解决

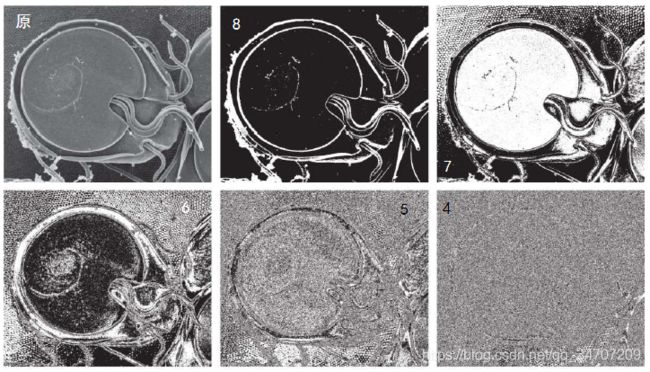
局部直方图处理
局部处理⇒隐藏细节,以上全局变换并不保证局部增强,细节被忽略,取n*n邻域内进行均衡或归一化得到被掩盖的细节
二阶矩即灰度方差,概率分母取 (MN-1) 参考无偏差估计,这里取 MN μ 2 ( r ) = σ 2 = ∑ i = 0 L − 1 [ r i − ∑ i = 0 L − 1 r i p ( r i ) ] 2 p ( r i ) \mu_2(r)=\sigma^2=\sum\limits_{i=0}^{L-1}[r_i-\sum\limits_{i=0}^{L-1}r_ip(r_i)]^2p(r_i) μ2(r)=σ2=i=0∑L−1[ri−i=0∑L−1rip(ri)]2p(ri)均值和方差总是有用的,尤其是在局部增强时,灵活!
eg:增强暗背景中的细节
1.根据灰度均值 m s x y ≤ k × m G m_{s_{xy}}\leq k\times m_G msxy≤k×mG 或 灰度方差 k 1 × σ G ≤ k 2 × σ s x y ≤ k 2 × σ G k_1\times\sigma_G\leq k_2\times \sigma_{s_{xy}}\leq k_2 \times\sigma_G k1×σG≤k2×σsxy≤k2×σG 选为待处理点, k 1 k_1 k1确定低阈值避免“增强”恒定区噪声
2.选定像素增强 g ( x , y ) = E ∙ f ( x , y ) g(x,y)=E \bullet f(x,y) g(x,y)=E∙f(x,y), E E E要调试,不能破坏视觉平衡
3.扫描,模板不宜过大,避免过大的计算量

空间滤波
相关(correlation):正向乘积求和
g ( x , y ) = ∑ s = − a a ∑ t = − b b w ( s , t ) f ( x + s , y + t ) = w ( x , y ) ⋆ f ( x , y ) g(x,y)=\sum\limits_{s=-a}^a\sum\limits_{t=-b}^bw(s,t)f(x+s,y+t)=w(x,y) \star f(x,y) g(x,y)=s=−a∑at=−b∑bw(s,t)f(x+s,y+t)=w(x,y)⋆f(x,y)
卷积(convolution):提前翻转180°乘积求和
g ( x , y ) = ∑ s = − a a ∑ t = − b b w ( s , t ) f ( x − s , y − t ) = w ( x , y ) ⭐ f ( x , y ) g(x,y)=\sum\limits_{s=-a}^a\sum\limits_{t=-b}^bw(s,t)f(x\color{red}-\color{black}s,y\color{red}-\color{black}t)=w(x,y) ⭐ f(x,y) g(x,y)=s=−a∑at=−b∑bw(s,t)f(x−s,y−t)=w(x,y)⭐f(x,y)
卷积滤波器、卷积模板、卷积核等模板与图像滑动乘积求和的术语并不一定真的卷积
n × n n \times n n×n大小的滤波器 = n 2 n^2 n2维向量 w ⃗ \vec w w,每个点和其邻域 = n 2 n^2 n2维向量 z ⃗ \vec z z,则相关或卷积矩阵形式: R = w 1 z 1 + . . . w n z n = ∑ k = 1 n 2 w k z k = w ⃗ T z ⃗ R=w_1z_1+...w_nz_n=\sum\limits_{k=1}^{n^2}w_kz_k=\vec w^T\vec z R=w1z1+...wnzn=k=1∑n2wkzk=wTz
如平滑滤波器 R = 1 n 2 ∑ i = 1 n 2 z i R=\frac{1}{n^2}\sum\limits_{i=1}^{n^2}z_i R=n21i=1∑n2zi,高斯滤波器 R = ∑ a = − n n ∑ b = − n n e − a 2 + b 2 2 σ 2 f ( x + a , y + b ) R=\sum\limits_{a=-n}^n\sum\limits_{b=-n}^ne^{-\frac{a^2+b^2}{2\sigma^2}}f(x+a,y+b) R=a=−n∑nb=−n∑ne−2σ2a2+b2f(x+a,y+b)
平滑空间滤波器
用法:模糊处理(桥接线段,去除细节),降低噪声
平滑线性滤波器(均值滤波器) g ( x , y ) = ∑ s = − a a ∑ t = − b b w ( s , t ) f ( x + s , y + t ) ∑ s = − a a ∑ t = − b b w ( s , t ) g(x,y)=\frac{\sum\limits_{s=-a}^{a}\sum\limits_{t=-b}^{b}w(s,t)f(x+s,y+t)}{\sum\limits_{s=-a}^{a}\sum\limits_{t=-b}^{b}w(s,t)} g(x,y)=s=−a∑at=−b∑bw(s,t)s=−a∑at=−b∑bw(s,t)f(x+s,y+t)其中 1 ∑ s = − a a ∑ t = − b b w ( s , t ) \frac{1}{\sum\limits_{s=-a}^{a}\sum\limits_{t=-b}^{b}w(s,t)} s=−a∑at=−b∑bw(s,t)1称作归一化常数, w ( x , y ) w(x,y) w(x,y)全部相等时称为盒状滤波器。
模板的大小取决于需要 平滑 或 融入背景 的对象尺寸决定
eg 提取目标对象的粗略图步骤:均值滤波 ⇒ 二值化(阈值=最高亮度的x%)

各向异性扩散平滑
较高斯模糊保留了边缘: I t + 1 ( x , y ) = I t ( x , y ) + λ ( c N ∇ N I t + c S ∇ S I t + c W ∇ W I t + c E ∇ E I t ) I_{t+1}(x,y)=I_t(x,y)+\lambda(c_N\nabla_N I_t+c_S\nabla_S I_t+c_W\nabla_W I_t+c_E\nabla_E I_t) It+1(x,y)=It(x,y)+λ(cN∇NIt+cS∇SIt+cW∇WIt+cE∇EIt)其中拉普拉斯算子是对各方向的导数: 北 向 导 数 ∇ N = I t ( x , y − 1 ) − I t ( x , y ) 南 向 导 数 ∇ S = I t ( x , y + 1 ) − I t ( x , y ) 西 向 导 数 ∇ W = I t ( x − 1 , y ) − I t ( x , y ) 东 向 导 数 ∇ E = I t ( x + 1 , y ) − I t ( x , y ) 北向导数\nabla_N=I_t(x,y-1)-I_t(x,y)\\ 南向导数\nabla_S=I_t(x,y+1)-I_t(x,y)\\ 西向导数\nabla_W=I_t(x-1,y)-I_t(x,y)\\ 东向导数\nabla_E=I_t(x+1,y)-I_t(x,y) 北向导数∇N=It(x,y−1)−It(x,y)南向导数∇S=It(x,y+1)−It(x,y)西向导数∇W=It(x−1,y)−It(x,y)东向导数∇E=It(x+1,y)−It(x,y)各向导数的权值,变化越大的方向权值越小: c N = e − ∇ N 2 k 2 c S = e − ∇ S 2 k 2 c W = e − ∇ W 2 k 2 c E = e − ∇ E 2 k 2 c_N=e^{-\frac{\nabla_N^2}{k^2}}\\c_S=e^{-\frac{\nabla_S^2}{k^2}}\\c_W=e^{-\frac{\nabla_W^2}{k^2}}\\c_E=e^{-\frac{\nabla_E^2}{k^2}} cN=e−k2∇N2cS=e−k2∇S2cW=e−k2∇W2cE=e−k2∇E2重复迭代指定的T次,后得到的结果能够保留倒数较大的边缘,而只模糊区域内的部分

统计排序(非线性)滤波器
| 统计方法 | 效果 |
|---|---|
| 中值滤波 | 去除较其邻域更亮或更暗,小于 m 2 2 \frac{m^2}{2} 2m2尺寸的区域 对脉冲噪声(椒盐噪声:叠加的黑白点)十分有效,模糊程度低 |
| 最大值滤波 | 搜寻图像中的最亮点 |
| 最小值滤波 | 搜寻图像中的最暗点 |
锐化空间滤波器
突出灰度的过渡部分,微分算子的响应强度 与 当前点突变程度 成正比(增强边缘和噪声)
一 阶 微 分 { 灰 度 恒 定 区 域 = 0 灰 度 变 化 处 非 0 变 化 中 非 0 ∂ f x = f ( x + 1 ) − f ( x ) 二 阶 微 分 { 灰 度 恒 定 区 域 = 0 灰 度 变 化 起 点 处 非 0 等 差 变 化 中 = 0 ∂ 2 f x 2 = f ( x + 1 ) + f ( x − 1 ) − 2 f ( x ) 一阶微分\begin{cases} 灰度恒定区域=0&\\ 灰度变化处非0&\\ 变化中非0 \end{cases} \frac{\partial f}{x}=f(x+1)-f(x)\\ 二阶微分 \begin{cases} 灰度恒定区域=0&\\ 灰度变化\color{red}起点\color{black}处非0&\\ \color{red}等差变化\color{black}中=0 \end{cases} \frac{\partial^2 f}{x^2}=f(x+1)+f(x-1)-2f(x) 一阶微分⎩⎪⎨⎪⎧灰度恒定区域=0灰度变化处非0变化中非0x∂f=f(x+1)−f(x)二阶微分⎩⎪⎨⎪⎧灰度恒定区域=0灰度变化起点处非0等差变化中=0x2∂2f=f(x+1)+f(x−1)−2f(x)
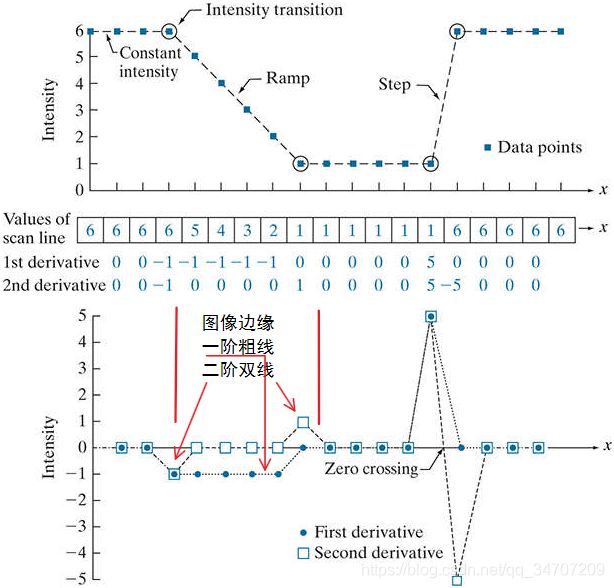
零交叉点(Zero-crossing)对边缘定位十分有效,二阶微分更适合锐化(增强细节)
各向同性二阶微分(拉普拉斯算子)
响应与图像的突变方向无关,旋转不变,如拉普拉斯算子: ∇ 2 f = ∂ 2 f ∂ x 2 + ∂ 2 f ∂ y 2 \nabla^2f=\frac{\partial^2 f}{\partial x^2}+\frac{\partial^2f}{\partial y^2} ∇2f=∂x2∂2f+∂y2∂2f离散形式: ∇ 2 f ( x , y ) = f ( x + 1 , y ) + f ( x − 1 , y ) + f ( x , y + 1 ) + f ( x , y − 1 ) − 4 f ( x , y ) \nabla^2f(x,y)=f(x+1,y)+f(x-1,y)+f(x,y+1)+f(x,y-1)-4f(x,y) ∇2f(x,y)=f(x+1,y)+f(x−1,y)+f(x,y+1)+f(x,y−1)−4f(x,y)滤波后的图像通常与其他图像相加减,注意符号!!
参考上图 f ( 2 ) > 0 , f ′ ′ ( 2 ) < 0 f(2)>0,f''(2)<0 f(2)>0,f′′(2)<0
为了使 + + +值更加 + + +, − - −更 − - −,锐化形式为 g ( 2 ) = f ( 2 ) − f ′ ′ ( 2 ) g(2)=f(2)-f''(2) g(2)=f(2)−f′′(2)
因此锐化操作意义是边界上强的更强,弱的更弱: g ( x , y ) = f ( x , y ) − ∇ ′ ′ f ( x , y ) g(x,y)=f(x,y)-\nabla''f(x,y) g(x,y)=f(x,y)−∇′′f(x,y)拉普拉斯运算 ⇒ 拉普拉斯结果 f − f m i n f-f_{min} f−fmin负值矫正 ⇒ 灰度范围拉伸“满” [ 0 , L − 1 ] [0,L-1] [0,L−1] ⇒ 标定后效果
⇓ \Downarrow ⇓
负值赋0 ⇒ 原图 + 拉普拉斯结果 ⇒ 完成锐化(如下)

unsharp masking 和 highboost filtering
模糊原始图像 ⇒ 模板=原图像-模糊图像 ⇒ 最终结果=原图像+模板 g ( x , y ) = f ( x , y ) + k ∗ g m a s k ( x , y ) = f ( x , y ) + k ∗ [ f ( x , y ) − f ‾ ( x , y ) ] g(x,y)=f(x,y)+k*g_{mask}(x,y)=f(x,y)+k*[f(x,y)-\overline f(x,y)] g(x,y)=f(x,y)+k∗gmask(x,y)=f(x,y)+k∗[f(x,y)−f(x,y)]k=1时称为 unsharp masking
k>1时称为 highboost filtering
这里我并不想将"unsharp masking"和"highboost filtering"翻译为“非锐化屏蔽"和”高提升滤波“,感觉并没有翻译出它们的“本意”。我认为,unsharp是说没有像先前那样求一二阶导,而是靠模糊图像这样的“反锐化操作”得到锐化操作所需要的掩膜,从而“减出”边缘,但本质还是对原图像进行了“锐化”(或者highboost filtering“加强锐化”),参见原文:
“Our objective is to sharpen this image using unsharp masking and highboost filtering.” -Example 3.21
k过大会导致<0,在图像上表现为暗晕轮,产生不好的结果

最终结果对模糊所用的低通滤波器要求并不高,只要主要特征别模糊到看不清就行

一阶微分(梯度)非线性图像锐化
梯度,既给出了变化最快的方向,也给出了变化的赋值,计算线性 ∇ f ≡ g r a n d ( f ) ≡ [ g x g y ] ≡ [ ∂ f ∂ x ∂ f ∂ y ] \nabla f \equiv grand(f) \equiv \begin{bmatrix}g_x\\g_y\end{bmatrix} \equiv \begin{bmatrix} \frac{\partial f}{\partial x}\\\frac{\partial f}{\partial y}\end{bmatrix} ∇f≡grand(f)≡[gxgy]≡[∂x∂f∂y∂f]这里先关注由幅值组成的梯度图像 M ( x , y ) = m a g ( ∇ f ) = g x 2 + g y 2 M(x,y)=mag(\nabla f)=\sqrt{g_x^2+g_y^2} M(x,y)=mag(∇f)=gx2+gy2
由于是几何平均数,所以非线性,幅值旋转不变
计算中使用绝对值近似也是可以的: M ( x , y ) ≈ ∣ g x ∣ + ∣ g y ∣ M(x,y)\approx |g_x|+|g_y| M(x,y)≈∣gx∣+∣gy∣
非线性,当且仅当 n × 90 ° n \times 90° n×90° 增量时是各向同性的
Roberts[1965]提出罗伯特交叉梯度算子,形式如下:
M ( x , y ) = [ f ( x + 1 , y + 1 ) − f ( x , y ) ] 2 + [ f ( x , y + 1 ) − f ( x + 1 , y ) ] 2 M(x,y)=\sqrt{[f(x+1,y+1)-f(x,y)]^2+[f(x,y+1)-f(x+1,y)]^2} M(x,y)=[f(x+1,y+1)−f(x,y)]2+[f(x,y+1)−f(x+1,y)]2 或 M ( x , y ) ≈ ∣ f ( x + 1 , y + 1 ) − f ( x , y ) ∣ + ∣ f ( x , y + 1 ) − f ( x + 1 , y ) ∣ M(x,y)\approx|f(x+1,y+1)-f(x,y)|+|f(x,y+1)-f(x+1,y)| M(x,y)≈∣f(x+1,y+1)−f(x,y)∣+∣f(x,y+1)−f(x+1,y)∣
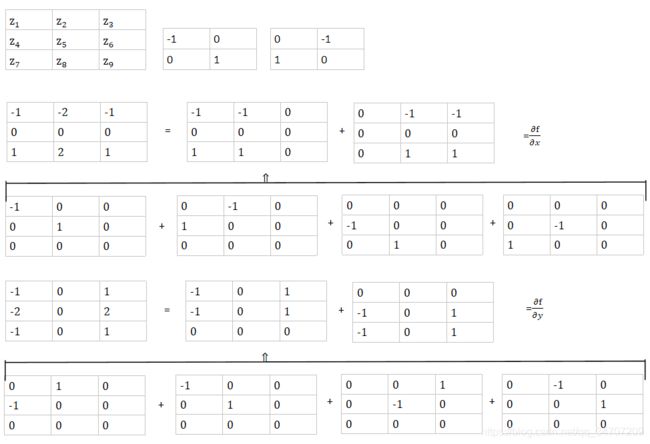
3*3大小的模板各项权值如图,称为soble算子,总权值=0符合离散微分定义灰度恒定区=0
低通,高通,带阻和带通滤波器
混合空间增强法
动态窄 高噪声 很难直接增强,方法:
Laplacian正比于变化的频率和幅度,突出(较小的)细节(和噪声) ⇒
梯度突出边缘(边缘通常较大,噪声和小细节较小,响应低) ⇒
梯度平滑去(掉平缓区域内)噪声,保留边缘 ⇒
梯度 ∗ * ∗Laplacian = 掩蔽 ⇒
增大动态范围(幂律变换、对数变换等)
模糊技术的应用
模糊集合在解决那些以不精确概描述的问题时,提供了一个基于人类知识的框架