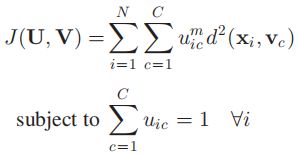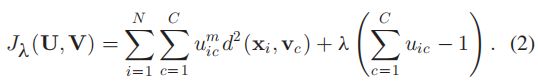FCM算法

FCM算法

一、FCM简述

FCM算法是基于对目标函数的优化基础上的一种数据聚类方法。聚类结果是每一个数据点对聚类中心的隶属程度，该隶属程度用一个数值来表示。该算法允许同一数据属于多个不同的类。
FCM算法是一种无监督的模糊聚类方法，在算法实现过程中不需要人为的干预。
这种算法的不足之处:首先，算法中需要设定一些参数，若参数的初始化选取的不合适，可能影响聚类结果的正确性;其次，当数据样本集合较大并且特征数目较多时，算法的实时性不太好。
K-means也叫硬C均值聚类（HCM），而FCM是模糊C均值聚类，它是HCM的延伸与拓展，HCM与FCM最大的区别在于隶属函数（划分矩阵）的取值不同，HCM的隶属函数只取两个值：0和1，而FCM的隶属函数可以取[0,1]之间的任何数。K-means和FCM都需要事先给定聚类的类别数，而FCM还需要选取恰当的加权指数α，α的选取对结果有一定的影响，α属于[0,+∞)。

二、算法描述

1、目标函数

2、算法优化

对于FCM算法采用拉格朗日乘子法进行优化：
迭代公式：

3、算法流程

4、Matlab实现

FCM1.m代码：

clear all;
close all;
ClustringMethod = 'FCM_test';
DataSet = input('input dataset:','s');
%% 读入不同的数据集
%% iris
% data=importdata([DataSet,'iris_data.txt']);
% id=importdata([DataSet,'iris_id.txt']);
% [data_num,data_dim]=size(data);
% id_label=min(id):max(id);
% center_num=max(id)-min(id)+1;
DataFile = ['D:\matlab_text\Data\',DataSet,'iris_data.txt'];
data = load(DataFile);%data
IdFile = ['D:\matlab_text\Data\',DataSet,'iris_id.txt'];
id = load(IdFile);%id
DataSet_name = 'iris';

% 读取数据信息
id_label = min(id):max(id);
[data_num,data_dim] = size(data);
center_num = max(id)-min(id)+1;
%% 参数设置
alpha=2;
threshold=1e-6;
loopnum = 100;
%% 输出文件
ResultDirection=['Result\',DataSet,'\',ClustringMethod,'\',DataSet_name];
if ~exist(ResultDirection,'dir')
    mkdir(ResultDirection);
end
Resultfile = [ResultDirection,'\alpha',num2str(alpha),'_',DataSet_name,'.txt'];
fp_result = fopen(Resultfile,'wt');
%% 将数据归一化到[0,1],采用min_max方法
data = (data-(ones(data_num,1)*min(data)))./(ones(data_num,1)*(max(data)-min(data)));
% ***************************************************************************************
% 避免陷入局部最优，重复计算100次
% ***************************************************************************************
for loop = 1:loopnum
    U = zeros(data_num,center_num);
    C = zeros(center_num,data_dim);
    % 初始化聚类中心--根据类中心初始化
    for i = 1:center_num
        temp = find(id==id_label(i));
        C(i,:) = data(temp(ceil(rand(1,1)*length(temp))),:);
    end
    iteration = 0;
    objfunc_old=0;
    %% Start----------FCM
    while(1)
        % 根据初始化的C计算隶属度U
        % 计算数据到聚类中心的距离
        distance_C = zeros(center_num,data_num);
        for i = 1:center_num
            distance_C(i,:) = ((bsxfun(@minus,C(i,:),data)).^2)*ones(1,data_dim)';
        end
        U = 1./(bsxfun(@times,(distance_C').^(1/(alpha-1)),sum((distance_C').^(-1/(alpha-1)),2)));
        U(distance_C'==0)=1;
        % 计算目标函数
        objfunc=sum(sum((U.^alpha).*(distance_C')));
        % 判断迭代终止条件
        if (abs(objfunc-objfunc_old)<threshold)
            break;
        end
        objfunc_old = objfunc;
        iteration = iteration + 1;
        % 更新聚类中心C
        Um = U.^alpha;
        C = bsxfun(@times,(Um')*data,((sum(Um))').^(-1));
    end
    %% End----------FCM
    % 将输出的隶属度U转换成id形式
    [~,id_U] = max(U,[],2);
    id_U = id_U - 1;
    % Compute the ACC
    [ACC,id_U_result] = Function_ACC( center_num,data_num,id_U,id_label,id );
    % Compute the NMI
    NMI = Function_NMI( id_U_result,id );
    % Output the ITE
    ITE = iteration;
    % Calculate the average value of evaluation indexes
    ACC_max = max(ACC,ACC_max);
    ACC_average = ACC_average + ACC/loopnum;
    NMI_average = NMI_average + NMI/loopnum;
    ITE_average = ITE_average + ITE/loopnum;
end
%% Output final results to .txt
fprintf(fp_result,'DataSet = %s\t',DataSet_name);
fprintf(fp_result,'ACC_max = %f\t',ACC_max);
fprintf(fp_result,'ACC_average = %f\t',ACC_average);
fprintf(fp_result,'NMI_average = %f\t',NMI_average);
fprintf(fp_result,'ITE_average = %f\n',ITE_average);
%% Output final results to terminal
fprintf('DataSet=%s\t ACC_max=%d\t ACC_average=%f\t NMI_average=%f\t ITE_average=%f\n',DataSet_name,ACC_max,ACC_average,NMI_average,ITE_average);

Function_ACC代码：

function [ accuracy_max,id_U_result ] = Function_ACC( center_num,data_num,id_U,id_label,id )
accuracy_max = 0;
% function_ACC 计算评价指标----准确率
% 全排列
id_permutation = perms(id_label);
id_temp = zeros(data_num,factorial(center_num));
for i = 1:factorial(center_num)
    for k = 1:center_num
        for j = 1:data_num
            if(id_U(j) == id_permutation(i,k))
                id_temp(j,i)=id_label(k);
            end
        end
    end
end
%分别计算每一种排列组合下的准确率
error = zeros(data_num,factorial(center_num));
for i = 1:data_num
    error(i,:) = (abs(id_temp(i,:)-id(i))>0)*1;%错误数
end
accuracy = max((data_num-sum(error))/data_num);
%得到准确率最高时的分类结果
id_U_result = id_temp(:,find((data_num-sum(error))/data_num==accuracy));
accuracy_max = max(accuracy,accuracy_max);
end

Function_NMI代码：

function [ NMI ] = Function_NMI( id_new,id_real )
% Function_NMI:hard clustering measure: normalized mutual information
% [data_num,center_num]=size(U);
data_num = length(id_real);
center_num = max(id_real(:))-min(id_real(:))+1;
id_label=min(id_real(:)):max(id_real(:));
%% compute the number of each cluster
Pn_id_new = zeros(1,center_num);
Pn_id_real = zeros(1,center_num);
P_id_new = zeros(1,center_num);
P_id_real = zeros(1,center_num);
for i = 1:center_num
    Pn_id_new(i) = length(find(id_new(:)==id_label(i)));
    Pn_id_real(i) = length(find(id_real(:)==id_label(i)));
    P_id_new(i) = length(find(id_new(:)==id_label(i)))/data_num;
    P_id_real(i) = length(find(id_real(:)==id_label(i)))/data_num;
end
%% compute entropy
H_new = 0;
H_real = 0;
for i = 1:center_num
    H_new = H_new - P_id_new(i)*log2(P_id_new(i));
    H_real = H_real-P_id_real(i)*log2(P_id_real(i));    
end
%% compute the number of mutual information
count_new_real=zeros(center_num,center_num);%同时隶属于Ri与Qj的数据点的个数
for i = 1:center_num
    for j = 1:center_num
        for n = 1:data_num
            if ((id_new(n) == id_label(i)) && (id_real(n) == id_label(j)))
                count_new_real(i,j) = count_new_real(i,j) + 1;
            end
        end
    end
end
P_new_real=count_new_real/data_num;
NMI=0;
for i=1:center_num
    for j=1:center_num
        if(P_new_real(i,j) ~= 0)
            NMI = NMI + P_new_real(i,j)*log2(P_new_real(i,j)/(P_id_new(i)*P_id_real(j)));
        end
    end
end
NMI = NMI/sqrt(H_new*H_real);
end

结果：

数据：
iris

三、参考文献

1.认识FCM算法
2.FCM算法的matlab程序
3.FCM理论详解