《基于网络的军用体系结构组合优化方法》阅读笔记
A Network-Based Portfolio Optimization Approach for Military System of Systems Architecting
摘要系统体系(System of Systems,SOS)架构是将系统整合为网络结构以实现特定目标的过程,这些目标具有独特的功能以及通过它们的互操作性实现的累积功能。如何在网络中交付能力对于基于能力的任务规划至关重要。为了通过将不同类型的系统架构成一个网络来满足不同的能力需求,我们用网络理论作为一个多目标优化模型来描述和分析SOS架构问题。更具体地说,我们从局部和全局的角度构建了一个三步能力交付模型来描述系统交互所造成的积极和消极后果。提出了一种具有可行性概念的三级响应模型,作为能力值的转换,以满足不同规模的作战需求,平衡新旧武器的部署。然后,结合所提出的模型设计了一些智能优化算法,分别逼近三个响应水平的帕累托前沿。一组数值研究的结果表明,节点较少的高效结构的性能优于全集结构,系统的部署应该综合考虑其整体结构影响,而不是单个系统的性能。此外,还定义和计算了四个体系级别属性作为补充,以使解决方案体系结构的价值更加全面。
本文的主要创新:结合能力交付模型和多目标优化方法提出了基于网络的能力价值生成和武器组合选择的方法
问题描述:
武器体系结构可以描述为武器 W W W和接口 I I I组合形成的图 G G G,从静态的角度看,场景下网络 G G G的值为 V ( S , G ) V(S,G) V(S,G),可以看作是三个响应水平下能力 C C C和性能 P P P的可行性。从动态的角度来看,武器网络是为完成作战任务而设计的。因此,任务调度理论、杀伤链理论、仿真方法等可以应用于 G G G的任务效能的制定,并将在以后的研究中加以研究。
G = { W , I } V ( S , G ) = { F ( C ( S , G ) , P ( S , G ) ) M ( S , G ) G=\left\{W,I\right\} \\ V(S,G)= \begin{cases} F(C(S,G),P(S,G)) \\ M(S,G) \end{cases} G={W,I}V(S,G)={F(C(S,G),P(S,G))M(S,G)
3 单一情景描述
3.1 场景与价值的定义
用两个衡量标准定义场景:
1)measures of effectiveness(MOE)有效性度量;
2)measures of performance(MOP)性能度量
数学描述为: S = { C , P } S=\left\{C,P\right\} S={C,P},其中,
[ C ] m × n = ( c 11 ⋯ c 1 n ⋮ ⋱ ⋮ c m 1 ⋯ c m n ) [ P ] m × n = ( p 11 ⋯ p 1 h ⋮ ⋱ ⋮ p m 1 ⋯ p m h ) \begin{aligned} [C]_{m\times n}=\left( \begin{matrix} c_{11}& \cdots& c_{1n}\\ \vdots& \ddots& \vdots\\ c_{m1}& \cdots& c_{mn}\\ \end{matrix} \right) \\ [P]_{m\times n}=\left( \begin{matrix} p_{11}& \cdots& p_{1h}\\ \vdots& \ddots& \vdots\\ p_{m1}& \cdots& p_{mh}\\ \end{matrix} \right) \end{aligned} [C]m×n=⎝⎜⎛c11⋮cm1⋯⋱⋯c1n⋮cmn⎠⎟⎞[P]m×n=⎝⎜⎛p11⋮pm1⋯⋱⋯p1h⋮pmh⎠⎟⎞表示一共有 m m m个武器, n n n个能力, h h h个性能指标。
(需要注意,效能矩阵是会随着作战环境和作战力量改变的;而性能矩阵是固定的)
3.2 系统网络建模
3.2.1 元功能节点建模
一个功能节点可以用以下一个数组来描述:
W = < T , O C , S , R > W=

3.2.2 接口建模
用故障率和互操作性水平两个度量来定义接口。功能边可以定义为: I = < I A , F R , I O L > I=
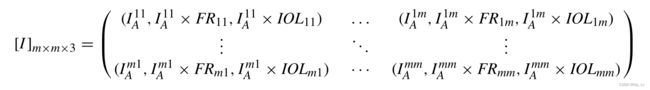
3.2.3 能力交付模型
3.2.3.1 直接通过接口提高价值
我们假设可以通过系统之间的接口获得额外的功能。系统的接口越多,可以提供的信息或其他资源就越多,从而帮助系统获得更强的战场意识和更好的支持。在网络理论中,系统拥有的接口数量可以用节点的度来表示。当元体系结构发生变化时,一些节点的退出和加入会导致边的增加或减少,从而影响到每个系统的接口数量。
我们采用假设:接口数量的增长将引起性能的小幅度指数增长,我们将第 i i i个系统的第 j j j个能力值变化记为:
c i j ∗ = c i j ( 1 + Δ ) d e g r e e i c_{ij}^*=c_{ij}(1+\Delta)^{degree_i} cij∗=cij(1+Δ)degreei Δ \Delta Δ表示度的增加量(定值), d e g r e e i degree_i degreei指第 i i i个系统在某个元结构中的度。
3.2.3.2 提供相同的能力提高价值
假设同时使用具有这种能力的多个系统将增加完成任务的概率。第 i i i个能力的完成可以表示为:
C i = 1 − ∏ j = 0 m ( 1 − c i j ∗ x j ) C_i=1-\prod_{j=0}^m{\left( 1-c_{ij}^*x_j \right)} Ci=1−j=0∏m(1−cij∗xj)其中 x j ∈ { 0 , 1 } x_j\in\left\{0,1\right\} xj∈{0,1},等于1表示元结构中包含第 j j j个武器,等于0则表示没有。
3.2.3.3 结构对价值产生影响
这些系统通过互联和互操作形成了一个完整的系统系统,体系结构可以对能力产生积极和消极的影响。如果将能力视为完成任务的概率或确定性,则可以利用架构带来的积极影响来挖掘剩余的不确定性,而负面影响将限制整体性能。
我们使用如下公式描述:
C i ∗ = [ C i + ( 1 − C i ) α ] ( 1 − β ) C_i^*=[C_i+(1-C_i)\alpha](1-\beta) Ci∗=[Ci+(1−Ci)α](1−β)其中, α \alpha α是描述整个网络结构的成功协作可以利用多少不确定性的系数,反映了间接协作有效性。 β \beta β是用来描述信息过载带来的负面影响的网络复杂性参数。
3.2.4 网络影响
下一步是给出两个结构参数 α \alpha α和 β \beta β的详细计算方法。我们将网络结构的影响,特别是对资源交换网络的影响分为两个方面:一个是一对系统之间的资源交换量,另一个是交换成功的概率。
3.2.4.1 协作成功
我们直接使用协作成功概率作为矩阵中的一个元素来估计结构影响参数,该概率本质上是不确定性的表示。在此之后,确定考虑所有协作系统对的总系统协作系数。
0 ≤ α = λ m a x ( F R S i ) / ( k − 1 ) ≤ 1 0\le\alpha=\lambda_{max}(FR_{S_i})/(k-1)\le1 0≤α=λmax(FRSi)/(k−1)≤1这里 F R S i FR_{S_i} FRSi表示某元结构的解 i i i的故障率矩阵, λ m a x \lambda_{max} λmax表示矩阵的最大特征值。
3.2.4.2 复杂性导致的限制
考虑到网络的复杂性带来的负面后果,结构越复杂,资源交换的负担越大,网络的有效性就会降低。按如下公式计算负面效应:
0 ≤ β = λ max ( I O L S i ) I O L max × k × ( 1 − 1 k ) ≤ 1 0\le\beta=\frac{\lambda _{\max}\left( IOL_{S_i} \right)}{IOL_{\max}\times k}\times \left( 1-\frac{1}{\sqrt{k}} \right) \le1 0≤β=IOLmax×kλmax(IOLSi)×(1−k1)≤1 I O L S i IOL_{S_i} IOLSi是解决方案 i i i的互操作性级别矩阵。λ最大值是最大特征值。 I O L max IOL_{\max} IOLmax是 I O L IOL IOL的最高评级。 ( 1 − 1 k ) / k \left( 1-\frac{1}{\sqrt{k}} \right)/k (1−k1)/k是考虑网络结构规模的修正系数。
4 多目标规划
我们提出了一个三级响应模型和一个可行性评估模型来解决问题,而不是简单地将能力或有效性最大化作为目标。根据不同的目标函数,不同的反应级别需要不同的武器配置。我们假设,一个好的武器结构不是由更好的性能定义的,而是由更好的可行性定义的,最终的火力结构应该是三个响应级别下的结构的叠加。
4.1 响应级别建模
在本研究中,将作战响应水平分为三个水平,并选择可行性作为衡量每个水平上的投资组合价值的指标。可行性是MOE和MOP的转换,表明在某些情况下什么级别的能力是最合适的。
对于反应级别1,它通常代表例行巡逻或守卫任务以及不需要部署高性能武器的小规模军事冲突的情况。在大多数情况下,小规模侦察能力或低级别火力威慑能力就足以满足任务需要。因此,通常会指派一些效率低但成本低的系统,或效率低但可生存性高的系统,或旧系统来完成这一级别的任务响应。我们假设,在这种情况下,能力值0.5是最合适的,而额外的能力将导致浪费。
对于第二级反应,任务的威胁显然会上升。敌人投入更多的兵力,目的更强,需要更有效的反应。在限制调度成本的前提下,将作战作战效能提高到较高水平,达到防出入或区域封锁的目的。在这种情况下,无人驾驶系统的低成本、高效率的特点显示出很强的适用性。因此,我们假设能力值0.75是最合适的,并且可行性函数形状显示右倾特征。
对于第3级反应,业务费用不再被视为部队设计的一个因素。随着战争规模的扩大,需要部署最强大的作战力量来击败敌人。采用logistic函数来描述能力最大化的要求。
可行性函数写作:

组合的最终价值定义为每个能力和性能指标的可行性总和:
o b j 1 ( p ) = m a x ( ∑ i = 1 n f e a s i b i l i t y ( C i ∗ , l e v e l ) + ∑ i = 1 h f e a s i b i l i t y ( P i , l e v e l ) ) obj1(p)=max(\sum_{i=1}^n{feasibility(C_i^*,level)+\sum_{i=1}^h{feasibility(P_i,level)}}) obj1(p)=max(i=1∑nfeasibility(Ci∗,level)+i=1∑hfeasibility(Pi,level))
我们选择作战成本或部署成本而不是采购成本作为另一个目标,而不是约束,因为在考虑未来作战力量的建设时,实现作战能力仍然是第一要务。我们可以考虑在达到预期能力的前提下将成本降至最低。如果将成本作为约束,则可能会限制解空间,从而可能错过最优解。此外,采购成本不适合作为行动部署问题的基础。武器系统的部署将涉及各种支援部队和资源的额外费用。因此,转而考虑部署成本更为合适。我们使用二次函数将部署成本转换为成本效率系数0-1,从而缩小低成本系统的效率差异,增加高成本武器的差异,这也增加了低成本武器之间的相互替代性。
o b j 2 ( p ) = m i n ( ∑ i = 1 m x i ( o c i o c m a x ) 2 ) obj2(p)=min(\sum_{i=1}^m{x_i(\frac{oc_i}{oc_{max}})^2}) obj2(p)=min(i=1∑mxi(ocmaxoci)2)
4.2 约束
在军事SOS架构的过程中,我们需要考虑以下约束。
1)完整性:为了保证组合能够满足要求的MoEs和MoPs,解需要满足以下条件:
∑ i = 1 m x i c i j ≥ 0 , j = 1 , . . . , n ∑ i = 1 m x i p i j ≥ 0 , j = 1 , . . . , h \sum_{i=1}^m{x_ic_{ij}}\ge0,\ \ j=1,...,n \\ \sum_{i=1}^m{x_ip_{ij}}\ge0,\ \ j=1,...,h i=1∑mxicij≥0, j=1,...,ni=1∑mxipij≥0, j=1,...,h
2)连通性:采用代数连通性作为图的连通性的重要指标,对作战系统的连通性进行了如下度量:
L = D − A A l g e b r a i c c o n n e c t i v i t y ( p ) = e i g e n v a l u e s e c o n d s m a l l e s t ( L ) ≥ 0 L=D-A \\ Algebraicconnectivity(p)=eigenvalue_{secondsmallest}(L)\ge0 L=D−AAlgebraicconnectivity(p)=eigenvaluesecondsmallest(L)≥0 D D D是度矩阵, A A A是图的邻接矩阵。该值的大小反映了整体图形连接的良好程度。它已被用于分析网络的健壮性和同步能力。
4.3 编码
4.4 算法步骤
p i j p_{ij} pij代表由系统 j j j在MoP矩阵中提供的第 i i i个MoP值。 P i P_i Pi是提供此功能的多个系统的综合值。 x j x_j xj是说明解决方案中是否存在系统 j j j。我们假设MoP的最终值是具有该度量的所有系统中的最大值,并且积分公式定义如下:
P i = max j = 1 , . . . , m ( p i j x j ) x j = 0 o r 1 P_i=\underset{j=1,...,m}{\max}\left( p_{ij}x_j \right) x_j=0\ \ or\ \ 1 Pi=j=1,...,mmax(pijxj)xj=0 or 1
具体的算法步骤如下:
1、定义参数:种群大小、迭代次数、交叉概率
2、种群初始化
3、对种群中的个体进行排序
4、交叉变异、产生子代
5、对父代和子代进行评估排序
6、生成新的种群
7、进化和迭代
4.5 结构融合
M e r g e ( n o n d o m i n a t e d ( l e v e l 1 ) , n o n d o m i n a t e d ( l e v e l 2 ) , n o n d o m i n a t e d ( l e v e l 3 ) ) Merge(nondominated(level1),nondominated(level2),nondominated(level3)) Merge(nondominated(level1),nondominated(level2),nondominated(level3))但本文并没有讨论如何融合
5 说明
5.1 初始数据生成方式
根据实际规划任务的特点,提出了一种基于规则的启发式测试数据生成方法来模拟实际数据特征。这些数据包括武器属性数据、武器能力数据、协作接口和属性。
首先,我们定义了武器的数量、MoE的数量和拖把的数量。每种武器随机生成1或2或3,代表武器类型。另外,其他基本属性的取值范围也根据类型进行定义。运营成本分为9个等级。根据上面的武器类型,类型1对应的是作战成本3-5(随机生成),生存概率设置在0.7-0.9之间,弹性成本设置在3-5之间。对于类型2,参考无人装备,作战成本设置为1-3,生存概率设置为0.3-0.6,弹性成本设置为1-3。对于类型3,如航空母舰,操作成本设置为6-9,生存概率设置为0.7-0.9,弹性成本设置为7-9。
价值矩阵是通过遍历MoE和MoP来确定是否以一定的概率建立的,该概率由MoE、MoP和武器的数量确定。如果确认关联,则根据武器类型设置能力值。构成系统在不同程度上提供了n个MoE和h个MoP的集合,其中零代表该武器对该指标没有贡献。对于不同的武器类型,该值分别设置为0.3-0.5、0.5-0.7和0.6-0.9。
最后,将生成接口矩阵。由于考虑的是无向关系,矩阵将是对称的。通过遍历矩阵的上三角,概率0.2被用来确定是否存在协同关系,也反映了现实中武器装备协同能力的平均水平。随后,为该接口随机生成0-1的成功协作概率和1-5的IOL。
5.2 输入
30个系统及其对应的类型、运营成本、存活率和恢复能力,系统与30个MoE、10个MoP之间的接口,以及武器间的协作关系。
5.3 体系属性
5.3.1灵活性
本文将灵活性定义为武器在相同能力范围内的可替代性。对于一种能力,能够提供这种能力的武器越多,在紧急情况下替代方案就越灵活。一件或多件武器的失败不会导致这种能力的失败。在实战中,灵活性尤为重要。能力的减少和能力的缺失是有本质区别的。能力的缺失,可能会造成连锁效应,导致整体作战能力瘫痪。因此,灵活性的高低是衡量结构好坏的一个重要指标。本文将系统的柔性定义为在所有能力下武器数量的平均水平。我们采用能力下装备数量的均值和方差两个指标来衡量投资组合的整体灵活性。
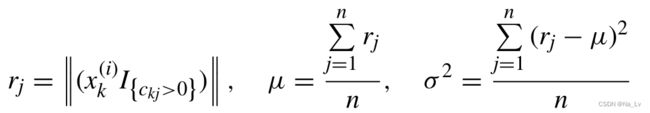
5.3.2 生存能力
本文对系统生存性的定义是所有武器的生存概率的加权和。权重是由武器的重要性决定的。我们假设,该架构中更重要的武器对SoS的整体生存能力有更大的影响。为了计算武器在SOS中的重要性,我们采用介数的概念作为度量来估计网络中节点的中心性。武器拥有的路径越多,它就越重要。路径的概念与实战作战中的OODA理论也是一致的,因此用中间度来描述武器在基于网络的SOS结构中的重要性是合理的。
B e t w e e n n e s s ( w j , s j ) = ∑ s ≠ w i ≠ t ∈ s j σ s t ( w i ) σ s t S u r v i v a b i l i t y j = ∑ i = 1 m N o r m a l i z e d ( B e t w e e n n e s s ( w i , s j ) ) s r i \begin{aligned} Betweenness(w_j,s_j)=\sum_{s\ne w_i \ne t \in s_j}{\frac{\sigma_{st}(w_i)}{\sigma_{st}}} \\ Survivability_j=\sum_{i=1}^{m}{Normalized(Betweenness(w_i,s_j))sr_i} \end{aligned} Betweenness(wj,sj)=s=wi=t∈sj∑σstσst(wi)Survivabilityj=i=1∑mNormalized(Betweenness(wi,sj))sri
5.3.3 恢复力
本文采用一种简化的复原力计算模型来衡量武器的复原力。对于每种武器,我们将复原力乘以武器在战斗中被摧毁的概率,然后将所有武器相加,作为投资组合的最终复原水平测量。
R e s i l i e n c e = ∑ i = 1 m ( 1 − s r i ) r i Resilience=\sum_{i=1}^m{(1-sr_i)r_i} Resilience=i=1∑m(1−sri)ri
5.3.4 稳健性
这里使用三个指标来描述体系结构的健壮性,包括当一个系统被移除时能力性能差异的最大值、最小值和D值。
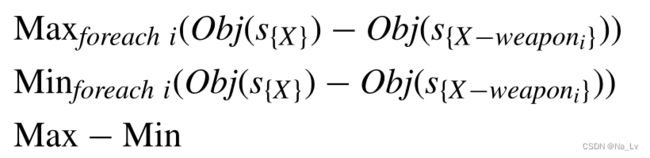
5.4 输出
5.5 结果分析
6 结论
系统体系结构在国防和军事领域有着广泛的实际应用。从这些系统的互操作性中获得的累积能力是CBP的基础,对于在战场上获得竞争优势至关重要。本研究利用基于网络的理论及其对称性度量,针对不同系统类型的SoS架构问题,提出了有效的解决方法。特别地,提出了一个双目标投资组合优化模型,并给出了逼近帕累托前沿的智能优化算法。估计能力的基础是中心性、中间度、度、网络协作和信息过载这些概念,这些因素会对能力产生产生积极和消极的影响。在此基础上,从不同角度提出了三种能力交付模型和三种响应水平可行性模型来计算目标。此外,还定义和计算了灵活性、可生存性、弹性和健壮性这四个SoS属性作为补充,以使解决方案体系结构的价值更加全面。
我们用一个简单的场景演示了该模型的应用。此场景体现了考虑网络影响的好处。特别是,正如预期的那样,在不使用成本或风险作为限制系统数量的约束的情况下,具有较少节点的高效网络结构比全集结构性能更好。这意味着一些系统在提供能力方面是冗余的,或者它们存在结构性的负面影响,这将导致太多的信息交换负担。功能要求可以是由一个高效的系统集通过它们的协作产生更高的能力而满足。实验还表明,以可行性为目标,而不是以能力或绩效为目标的好处:可以得到面向目的的结构,并且可以在特定的功能应用中考虑一些低性能和中等性能的系统。通过一系列的数值研究,对求解结果进行了比较,并分析了能力生成的内在机理。讨论了几个方面的问题。可以观察到,一些节点具有很大的结构影响,而一些节点是冗余的,以提供能力。实验表明,武器的部署应综合考虑整个SoS结构和响应水平,而不是单个系统的性能。网络中的任何微小变化都可能导致最终结果的巨大差异。本文提出的模型提供了一个在网络中心战环境下如何从SoS中产生能力的一瞥,以及在进行SoS架构时DM应该考虑什么。
本文的研究启发了基于网络的武器组合选择和SOS能力生成机制的研究。未来的研究方向包括允许具有不同偏好的多场景优化、基于多准则决策方法的SoS属性的非支配解之间的进一步权衡、任务网络建模以及动态演化的体系结构问题。这些挑战必将有助于扩大这一方法,以解决更广泛的问题。
