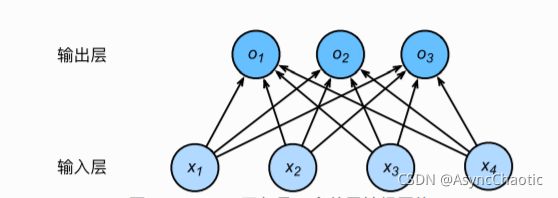
Softmax回归模型

Softmax回归模型一般用于分类任务，它的输出值个数等于标签里的类别数。w权重参数等于输入特征值*输出值个数，偏差参数b等于输出值个数。Softmax回归同线性回归一样是一个单层神经网络，输出层也是一个全连接层。

分类任务本是将输出值作为对预测类别i的置信度，在softmax模型中引用了softmax运算符，将输出值转变为正且和为1的概率分布

softmax回归对样本i分类的矢量计算表达式

softmax运算将输出变为了一个合法的类别预测分布，训练样本的真实标签也可以变为类别分布表达：对于样本i，我们构造向量 ，它属于哪个类别，就将那个类别的值置为1，其余为0（类似于线代中的单位向量）。

交叉熵损失函数：交叉熵能够衡量同一个随机变量中的两个不同概率分布的差异程度

交叉熵损失函数原理详解_Cigar-CSDN博客_交叉熵损失函数(里面很多算式少一个左括号)

FASHION-MNIST数据集的下载和配置

import torch
import torchvision
import torchvision.transforms as transforms
import matplotlib.pyplot as plt
import time
import sys
# 下载训练集和测试集
from IPython import display

mnist_train =torchvision.datasets.FashionMNIST(root='~/Datasets/FashionMNIST',train=True, download=True, transform=transforms.ToTensor())
mnist_test =torchvision.datasets.FashionMNIST(root='~/Datasets/FashionMNIST',train=False, download=True, transform=transforms.ToTensor())

# print(type(mnist_train))
# print(len(mnist_train), len(mnist_test))
#
# feature, label = mnist_train[0]
# print(feature.shape, label) # Channel x Height X Width

# 将数值标签转化为文本标签
def get_fashion_mnist_labels(labels):
 text_labels = ['t-shirt', 'trouser', 'pullover', 'dress','coat','sandal', 'shirt', 'sneaker', 'bag', 'ankleboot']
 return [text_labels[int(i)] for i in labels]

def use_svg_display():
    # 用矢量图显示
    display.set_matplotlib_formats('svg')
# def set_figsize(figsize=(3.5, 2.5)):
#     use_svg_display()
#  # 设置图的尺⼨
#     plt.rcParams['figure.figsize'] = figsize
#     set_figsize()
#     plt.scatter(features[:, 1].numpy(), labels.numpy(), 1)
#     plt.show()

def show_fashion_mnist(images, labels):
    use_svg_display()
 # 这⾥的_表示我们忽略（不使⽤）的变量
    _, figs = plt.subplots(1, len(images), figsize=(12, 12))
    for f, img, lbl in zip(figs, images, labels):
        f.imshow(img.view((28, 28)).numpy())
        f.set_title(lbl)
        f.axes.get_xaxis().set_visible(False)
        f.axes.get_yaxis().set_visible(False)
    plt.show()

X, y = [], []
for i in range(10):
 X.append(mnist_train[i][0])
 y.append(mnist_train[i][1])
show_fashion_mnist(X, get_fashion_mnist_labels(y))

# 创建一个DataLoader实例小批量读取图形数据
batch_size = 256
if sys.platform.startswith('win'):
    num_workers = 0 # 0表示不⽤额外的进程来加速读取数据
else:
    num_workers = 4
train_iter = torch.utils.data.DataLoader(mnist_train,batch_size=batch_size, shuffle=True, num_workers=num_workers)
test_iter = torch.utils.data.DataLoader(mnist_test,batch_size=batch_size, shuffle=False, num_workers=num_workers)

# 测试读取一遍训练集所需的时间
start = time.time()
for X, y in train_iter:
    continue
print('%.2f sec' % (time.time() - start))

torchvision包：torchvision 是PyTorch中专门用来处理图像的库。这个包中有四个大类。

torchvision.datasets/torchvision.models/torchvision.transforms/torchvision.utils

Softmax回归的一个小Demo

import torch
from torch import nn
from torch.nn import init
import numpy as np
import sys
sys.path.append("..")
import d2lzh_pytorch as d2l

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

num_inputs = 784
num_outputs = 10 #这个10既是输出维度也是全连接层的神经元个数
class LinearNet(nn.Module):
    def __init__(self, num_inputs, num_outputs):
        super(LinearNet, self).__init__()
        self.linear = nn.Linear(num_inputs, num_outputs)
    def forward(self, x):  # x shape: (batch, 1, 28, 28) x是数据集，要将其转化为784维才可以放入设置好的全连接层
        y = self.linear(x.view(x.shape[0], -1))
        return y

net = LinearNet(num_inputs, num_outputs)

class FlattenLayer(nn.Module):
    def __init__(self):
        super(FlattenLayer, self).__init__()
    def forward(self, x): # x shape: (batch, *, *, ...)
        return x.view(x.shape[0], -1)

from collections import OrderedDict
net = nn.Sequential(
 # FlattenLayer(),
 # nn.Linear(num_inputs, num_outputs)
    OrderedDict([
        ('flatten', FlattenLayer()),
        ('linear', nn.Linear(num_inputs, num_outputs))])
    )
#初始化参数 均值0，标准差为0.01的正态分布随机初始化参数
init.normal_(net.linear.weight, mean=0, std=0.01)
init.constant_(net.linear.bias, val=0)

loss = nn.CrossEntropyLoss()

optimizer = torch.optim.SGD(net.parameters(), lr=0.1)

num_epochs = 5
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs,batch_size, None, None, optimizer)

X, y = iter(test_iter).next()
true_labels = d2l.get_fashion_mnist_labels(y.numpy())
pred_labels =d2l.get_fashion_mnist_labels(net(X).argmax(dim=1).numpy())
titles = [true + '\n' + pred for true, pred in zip(true_labels,pred_labels)]
d2l.show_fashion_mnist(X[0:9], titles[0:9])


d21zh:


import sys
import torchvision
import torchvision.transforms as transforms
import torch
from IPython import display
from matplotlib import pyplot as plt


def sgd(params, lr, batch_size): # 本函数已保存在d2lzh_pytorch包中⽅便以后使⽤
    for param in params:
        param.data -= lr * param.grad / batch_size

def load_data_fashion_mnist(batch_size):
    mnist_train = torchvision.datasets.FashionMNIST(root='~/Datasets/FashionMNIST', train=True, download=True,transform=transforms.ToTensor())
    mnist_test = torchvision.datasets.FashionMNIST(root='~/Datasets/FashionMNIST', train=False, download=True,transform=transforms.ToTensor())
    if sys.platform.startswith('win'):
        num_workers = 0  # 0表示不⽤额外的进程来加速读取数据
    else:
        num_workers = 4
    train_iter = torch.utils.data.DataLoader(mnist_train, batch_size=batch_size, shuffle=True, num_workers=num_workers)
    test_iter = torch.utils.data.DataLoader(mnist_test, batch_size=batch_size, shuffle=False, num_workers=num_workers)
    return train_iter,test_iter

# 本函数已保存在d2lzh_pytorch包中⽅便以后使⽤。该函数将被逐步改进：它的完整实现将在“图像增⼴”⼀节中描述
def evaluate_accuracy(data_iter, net):
    acc_sum, n = 0.0, 0
    for X, y in data_iter:
        acc_sum += (net(X).argmax(dim=1) == y).float().sum().item()
        n += y.shape[0]
    return acc_sum / n

num_epochs, lr = 5, 0.1
# 本函数已保存在d2lzh包中⽅便以后使⽤
def train_ch3(net, train_iter, test_iter, loss, num_epochs,batch_size,params=None, lr=None, optimizer=None):
    for epoch in range(num_epochs):
        train_l_sum, train_acc_sum, n = 0.0, 0.0, 0
        for X, y in train_iter:
            y_hat = net(X)
            l = loss(y_hat, y).sum() #这里的loss函数是corssentropyloss函数

        # 梯度清零
            if optimizer is not None:
                optimizer.zero_grad()
            elif params is not None and params[0].grad is not None:
                for param in params:
                    param.grad.data.zero_()

            l.backward()
            if optimizer is None:
                sgd(params, lr, batch_size)
            else:
                optimizer.step()  # “softmax回归的简洁实现”⼀节将⽤到
            train_l_sum += l.item() #item()取出单元素张量的元素值并返回该值，保持原元素类型不变。
            train_acc_sum += (y_hat.argmax(dim=1) ==y).sum().item() #argmax()返回指定维度的最大值的索引。计算正确率
            n += y.shape[0]
        test_acc = evaluate_accuracy(test_iter, net)
        print('epoch %d, loss %.4f, train acc %.3f, test acc %.3f'% (epoch + 1, train_l_sum / n, train_acc_sum / n,test_acc))

def get_fashion_mnist_labels(labels):
    text_labels = ['t-shirt', 'trouser', 'pullover', 'dress','coat','sandal', 'shirt', 'sneaker', 'bag', 'ankleboot']
    return [text_labels[int(i)] for i in labels]

def use_svg_display():
    # 用矢量图显示
    display.set_matplotlib_formats('svg')

def show_fashion_mnist(images, labels):
    use_svg_display()
 # 这⾥的_表示我们忽略（不使⽤）的变量
    _, figs = plt.subplots(1, len(images), figsize=(12, 12))
    for f, img, lbl in zip(figs, images, labels):
        f.imshow(img.view((28, 28)).numpy())
        f.set_title(lbl)
        f.axes.get_xaxis().set_visible(False)
        f.axes.get_yaxis().set_visible(False)
    plt.show()

引自 PyTorch的nn.Linear（）详解_风雪夜归人o的博客-CSDN博客_nn.linear

PyTorch的nn.Linear（）是用于设置网络中的全连接层的，需要注意在二维图像处理的任务中，全连接层的输入与输出一般都设置为二维张量，形状通常为[batch_size, size]，不同于卷积层要求输入输出是四维张量。其用法与形参说明如下：

  in_features指的是输入的二维张量的大小，即输入的[batch_size, size]中的size。
  out_features指的是输出的二维张量的大小，即输出的二维张量的形状为[batch_size，output_size]，当然，它也代表了该全连接层的神经元个数。
  从输入输出的张量的shape角度来理解，相当于一个输入为[batch_size, in_features]的张量变换成了[batch_size, out_features]的输出张量。
在PyTorch中view函数作用为重构张量的维度.

import torch
tt1=torch.tensor([-0.3623,-0.6115,0.7283,0.4699,2.3261,0.1599])
result=tt1.view(3,2)
tensor([[-0.3623, -0.6115],
        [ 0.7283,  0.4699],
        [ 2.3261,  0.1599]])

torch.view(参数a,参数b,.....)，其中参数a=3,参数b=2决定了将一维的tt1重构成3*2维的张量。

在pytorch中的图片一般是以(Batch_size,通道数，图片高度，图片宽度)。如果一个图片看成一个四维张量的话，它的形状是(Batch_size,通道数，图片高度，图片宽度)，分别代表四个维度，shape[0]，shape[1]，shape[2]，shape[3]，你可以输出任一个维度的内容数。

X.view(-1)中的-1本意是根据另外一个数来自动调整维度，但是这里只有一个维度，因此就会将X里面的所有维度数据转化成一维的，并且按先后顺序排列。

因为每一个module都继承于nn.Module,都会实现__call__与forward函数

nn.Sequential
A sequential container. Modules will be added to it in the order they are passed in the constructor. Alternatively, an ordered dict of modules can also be passed in.

一个有序的容器，神经网络模块将按照在传入构造器的顺序依次被添加到计算图中执行，同时以神经网络模块为元素的有序字典也可以作为传入参数。
pytorch系列7 -----nn.Sequential讲解_墨流觞的博客-CSDN博客_nn.sequential

分开定义softmax运算和交叉熵损失函数可能会造成数值不稳定

dim的不同值表示不同维度。特别的在dim=0表示二维中的行，dim=1在二维矩阵中表示列。广泛的来说，我们不管一个矩阵是几维的。