神经网络学习（三）：解偏微分方程

前言

        在完成了常微分的数值解之后，我开始如法炮制的来解偏微分，我觉得解法上是一样的，都直接使用autograd就可以了，所以理论是难度并不大（虽然实际上我是花的时间最长的），只不过需要注意的细节比较多，所以模型卡了很久都没有效果，让我都怀疑人生了，今天终于找到了问题！所以把整个过程介绍一下

        今天选择的偏微分方程为Burgers方程，在Dirichlet条件下求数值解，具体形式为：

训练流程

1.定义网络

        这里定义网络的方法还是和第二篇是一样的，有需要可以去看看第二篇文章

神经网络学习（二）：解常微分方程_lny161224的博客-CSDN博客前言在完成了函数拟合之后，现在考虑常微分方程：给定一个常微分方程，让你求得这个微分方程的近似解（在给定的初值条件下）。以前都是用数学的知识来解决（这让我想起了大一在立人楼上常微分的夜晚），现在有了神经网络，我们用深度学习的方法来解决它试一试。 本次选择的微分方程是训练流程1.定义网络 本来是想使用之前定义的网络，但是觉得以后反正要用就规范化一下这个网络，增加一下可操作性（其实是因为当时我人在办公室笔记本上没有代码就直接重写了），在初始化中增加...https://blog.csdn.net/lny161224/article/details/120499386

        因为输入是二维的（由t,x形成的二维矩阵），所以把输入层改为2即可。

class Net(nn.Module):
    def __init__(self, NL, NN):
        # NL是有多少层隐藏层
        # NN是每层的神经元数量
        super(Net, self).__init__()
        self.input_layer = nn.Linear(2, NN)
        self.hidden_layer = nn.ModuleList([nn.Linear(NN, NN) for i in range(NL)])
        self.output_layer = nn.Linear(NN, 1)

    def forward(self, x):
        o = self.act(self.input_layer(x))
        for i, li in enumerate(self.hidden_layer):
            o = self.act(li(o))
        out = self.output_layer(o)
        return out

    def act(self, x):
        return torch.tanh(x)

2.初始化样本集

        与之前不同的是，这里的样本分为了两类，一类是用于训练用的随机二维样本，另一类是满足初值条件和边界条件的特殊二维样本，所以为了方便整理，定义了一个sample函数来生成样本集

def sample(size):
    x = torch.cat((torch.rand([size, 1]), torch.full([size, 1], -1) + torch.rand([size, 1]) * 2), dim=1)
    # 因为后面有sin(πx),所以这里得先把x存下来，并且保证和带入初值的x_initial(t,x)的x部分是相同的
    x_init = torch.full([size, 1], -1) + torch.rand([size, 1]) * 2
    x_initial = torch.cat((torch.zeros(size, 1), x_init), dim=1)
    x_boundary_left = torch.cat((torch.rand([size, 1]), torch.full([size, 1], -1)), dim=1)
    x_boundary_right = torch.cat((torch.rand([size, 1]), torch.ones([size, 1])), dim=1)
    return x, x_initial, x_init, x_boundary_left, x_boundary_right

        这里处理上有个手法，因为所以，生成t的时候直接用torch.rand()就可以,而对于x，我想到的方法就是从-1开始，生成[0,2]的随机结果然后合在一起，那么结果就是在[-1,1]上的（虽然忘了在哪学的，但是感觉就该这么处理嘻嘻嘻）

        这里使用了torch.cat()将两个维度拼在一起，形成了想要的样本集。这里要着重讲一下初值条件，因为初值条件是在t = 0时得到的只跟x有关的函数，所以生成初值样本集的时候一定要注意后面用于计算的和所对应的x应该是一样的，这里就直接保存了随机结果x_init，这样保证了一致性，且把x_init传了回来，这个在后面会提到为什么会传过来

3.定义损失

        还是跟（二）一样，将近似函数的损失（误差）和初值、边界条件的误差加在一起作为其损失，处理如下

        loss1 = loss_fn(dt + y_train * dx, (0.01 / np.pi) * dxx)
        loss2 = loss_fn(net(x_initial), -1 * torch.sin(np.pi * x_init))
        loss3 = loss_fn(net(x_left), torch.zeros([size, 1]))
        loss4 = loss_fn(net(x_right), torch.zeros([size, 1]))
        loss = loss1 + loss2 + loss3 + loss4

        这里有两个地方需要注意：

        a)从思路上来说我们应该吧等式两边移到一边，然后使他和0对比作为损失，只不过这样操作的话就需要想loss3和loss4一样生成同样size的零矩阵，为了节省空间（实际是为了偷懒），等式两边都放一部分，这样就不需要再额外生成了

        b)注意这个loss2,等式左边是在网络下得到的初值结果，右边是同样的x的情况下得到的值，首先得保证这两个对应的x是一样的，其次需要注意的是右边只需要传入x这一个维度，不需要u（卡了几天没解决都是因为这个地方），因此才需要生成样本的时候传回x_init

4.函数求偏导

        这里充分利用了autograd自动求梯度来实现，二阶导就是在一阶导的情况下再来一次

        x = Variable(x_train, requires_grad=True)
        d = torch.autograd.grad(net(x), x, grad_outputs=torch.ones_like(net(x)), create_graph=True)
        dt = d[0][:, 0].unsqueeze(-1)
        dx = d[0][:, 1].unsqueeze(-1)
        dxx = torch.autograd.grad(dx, x, grad_outputs=torch.ones_like(dx), create_graph=True)[0][:, 1].unsqueeze(-1)
        # 先把该求的求完然后清零，减少影响（虽然不知道有没有用）
        optimizer.zero_grad()

5.训练模型

    for i in range(10 ** 4):
        x = Variable(x_train, requires_grad=True)
        d = torch.autograd.grad(net(x), x, grad_outputs=torch.ones_like(net(x)), create_graph=True)
        dt = d[0][:, 0].unsqueeze(-1)
        dx = d[0][:, 1].unsqueeze(-1)
        dxx = torch.autograd.grad(dx, x, grad_outputs=torch.ones_like(dx), create_graph=True)[0][:, 1].unsqueeze(-1)
        # 先把该求的求完然后清零，减少影响（虽然不知道有没有用）
        optimizer.zero_grad()
        y_train = net(x)
        # 为了少生成几个零矩阵，所以计算损失的时候把条件移到两边了
        loss1 = loss_fn(dt + y_train * dx, (0.01 / np.pi) * dxx)
        loss2 = loss_fn(net(x_initial), -1 * torch.sin(np.pi * x_init))
        loss3 = loss_fn(net(x_left), torch.zeros([size, 1]))
        loss4 = loss_fn(net(x_right), torch.zeros([size, 1]))
        loss = loss1 + loss2 + loss3 + loss4
        loss.backward()
        optimizer.step()
        if i % 1000 == 0:
            print(f'step: {i}  loss = {loss.item()}')

6.数据可视化

        因为自变量成为了2维，所以想要表示u(t,x)得用3D来画图，并把图像保存下来

    T, X = np.meshgrid(t, x, indexing='ij')
    pred_surface = np.reshape(pred, (t.shape[0], x.shape[0]))
    Exact_surface = np.reshape(Exact, (t.shape[0], x.shape[0]))

    # plot the approximated values
    fig = plt.figure()
    ax = fig.add_subplot(projection='3d')
    ax.set_zlim([-1, 1])
    ax.plot_surface(T, X, pred_surface, cmap=cm.RdYlBu_r, edgecolor='blue', linewidth=0.0003, antialiased=True)
    ax.set_xlabel('t')
    ax.set_ylabel('x')
    ax.set_zlabel('u')
    plt.savefig('Preddata.png')
    plt.close(fig)

7.训练结果

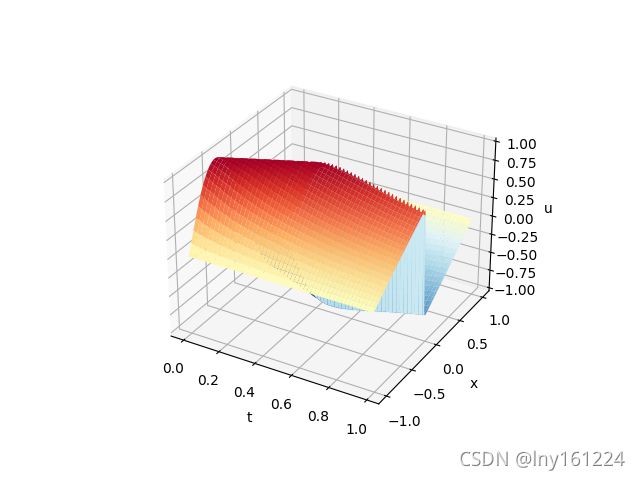
        为了知道模型是不是正确的，我找了PINNs里给出的正确解，并且在同样的范围内用模型求解，附图如下：

 （模型与真实结果对比图：左边是真实数据集形成的u(t,x），右边是预测模型生成的u(t,x)）

         可以看到效果还是挺好的，些许的不同可能是因为我的样本点选的比较少，可以加大样本点数量达到更好效果

总结与期望

         利用深度学习来求偏微分方程数值解，只要知道如何将导数表示出来，就可以很好地表示出损失剩下的就只需要交给你的网络，让网络慢慢去学习更新优化参数，最后获得比较满意的结果。

        本文实现了PINNs里Burgers公式求解的代码复现，其实这也是我最开始遇到的问题，前面两篇就是为了解决这个问题做的铺垫（因为模型效果一直不好，所以想到简化问题看能不能实现），结果发现就是因为损失那个地方被sin(πx）整了一手，这里的x并非输入层得到的x（输入层得到的实际是u(t,x)，而sin(πx）是输入层第二维的x），总的来说，收获颇丰，很多东西都是自己一点一点摸索出来的，当然也是学习了知乎大佬的解法，慢慢找到正确的解法，再次感谢！

深度学习求解偏微分方程系列一：Deep Galerkin Method - 知乎我们接下来将用一个系列的文章，介绍使用神经网络的办法求解偏微分方程。这是本系列的第一篇，介绍Deep Galerkin Method (DGM）。我们首先介绍DGM的理论。最后我们使用Python求解一个热传播方程。1. 简介偏微分方…https://zhuanlan.zhihu.com/p/359328643        接下来准备考虑实现的是PINNs中的第二个问题：在数据驱动下的探索发现，即得到了正确的数据集u(t,x)，但是偏微分方程中是带了未知参数的情况，通过神经网络来求得参数的方法

源代码

import torch
import torch.nn as nn
import numpy as np
import matplotlib.pyplot as plt
import torch.optim as optim
from torch.autograd import Variable
from matplotlib import cm
import scipy.io


class Net(nn.Module):
    def __init__(self, NL, NN):
        # NL是有多少层隐藏层
        # NN是每层的神经元数量
        super(Net, self).__init__()
        self.input_layer = nn.Linear(2, NN)
        self.hidden_layer = nn.ModuleList([nn.Linear(NN, NN) for i in range(NL)])
        self.output_layer = nn.Linear(NN, 1)

    def forward(self, x):
        o = self.act(self.input_layer(x))
        for i, li in enumerate(self.hidden_layer):
            o = self.act(li(o))
        out = self.output_layer(o)
        return out

    def act(self, x):
        return torch.tanh(x)


"""
用来生成拟合函数、初值条件、边界条件的输入
这里是用torch.rand随机生成，并且根据取值范围调整了表达式
"""


def sample(size):
    x = torch.cat((torch.rand([size, 1]), torch.full([size, 1], -1) + torch.rand([size, 1]) * 2), dim=1)
    # 因为后面有sin(πx),所以这里得先把x存下来，并且保证和带入初值的x_initial(t,x)的x部分是相同的
    x_init = torch.full([size, 1], -1) + torch.rand([size, 1]) * 2
    x_initial = torch.cat((torch.zeros(size, 1), x_init), dim=1)
    x_boundary_left = torch.cat((torch.rand([size, 1]), torch.full([size, 1], -1)), dim=1)
    x_boundary_right = torch.cat((torch.rand([size, 1]), torch.ones([size, 1])), dim=1)
    return x, x_initial, x_init, x_boundary_left, x_boundary_right


if __name__ == '__main__':
    size = 2000
    lr = 1e-4
    x_train, x_initial, x_init, x_left, x_right = sample(size)
    net = Net(NL=4, NN=20)
    optimizer = optim.Adam(net.parameters(), lr)
    loss_fn = nn.MSELoss(reduction='mean')
    for i in range(10 ** 4):
        x = Variable(x_train, requires_grad=True)
        d = torch.autograd.grad(net(x), x, grad_outputs=torch.ones_like(net(x)), create_graph=True)
        dt = d[0][:, 0].unsqueeze(-1)
        dx = d[0][:, 1].unsqueeze(-1)
        dxx = torch.autograd.grad(dx, x, grad_outputs=torch.ones_like(dx), create_graph=True)[0][:, 1].unsqueeze(-1)
        # 先把该求的求完然后清零，减少影响（虽然不知道有没有用）
        optimizer.zero_grad()
        y_train = net(x)
        # 为了少生成几个零矩阵，所以计算损失的时候把条件移到两边了
        loss1 = loss_fn(dt + y_train * dx, (0.01 / np.pi) * dxx)
        loss2 = loss_fn(net(x_initial), -1 * torch.sin(np.pi * x_init))
        loss3 = loss_fn(net(x_left), torch.zeros([size, 1]))
        loss4 = loss_fn(net(x_right), torch.zeros([size, 1]))
        loss = loss1 + loss2 + loss3 + loss4
        loss.backward()
        optimizer.step()
        if i % 1000 == 0:
            print(f'step: {i}  loss = {loss.item()}')
    """
    接下来引入正确解 画图进行比较
    """
    data = scipy.io.loadmat('burgers_shock.mat')
    t = data['t'].flatten()[:, None]
    x = data['x'].flatten()[:, None]
    Exact = np.real(data['usol']).T

    temp = np.empty((2, 1))
    i = 0
    j = 0
    pred = np.zeros((100, 256))
    for _t in t:
        temp[0] = _t
        for _x in x:
            temp[1] = _x
            ctemp = torch.Tensor(temp.reshape(1, -1))
            pred[i][j] = net(ctemp).detach().cpu().numpy()
            j = j + 1
            if j == 256:
                j = 0
        i = i + 1
    T, X = np.meshgrid(t, x, indexing='ij')
    pred_surface = np.reshape(pred, (t.shape[0], x.shape[0]))
    Exact_surface = np.reshape(Exact, (t.shape[0], x.shape[0]))

    # plot the approximated values
    fig = plt.figure()
    ax = fig.add_subplot(projection='3d')
    ax.set_zlim([-1, 1])
    ax.plot_surface(T, X, pred_surface, cmap=cm.RdYlBu_r, edgecolor='blue', linewidth=0.0003, antialiased=True)
    ax.set_xlabel('t')
    ax.set_ylabel('x')
    ax.set_zlabel('u')
    plt.savefig('Preddata.png')
    plt.close(fig)
    # plot the exact solution
    fig = plt.figure()
    ax = fig.add_subplot(projection='3d')
    ax.set_zlim([-1, 1])
    ax.plot_surface(T, X, Exact_surface, cmap=cm.RdYlBu_r, edgecolor='blue', linewidth=0.0003, antialiased=True)
    ax.set_xlabel('t')
    ax.set_ylabel('x')
    ax.set_zlabel('u')
    plt.savefig('Turedata.png')
    plt.close(fig)