决策树可视化和计算原理
1.建模和可视化
1.1首先,创建数据用于决策树
# 1.导包
import numpy as np
from sklearn.tree import DecisionTreeClassifier
import pandas as pd
from sklearn import tree
import graphviz
import re# 创建数据
y = np.array(list('NYYYYYNYYN'))# 是否是真实用户
X =pd.DataFrame(
{
'日志密度':list('sslmlmmlms'),
'好友密度':list('slmmmlsmss'),
'真实头像':list('NYYYYNYYYY')
}
)
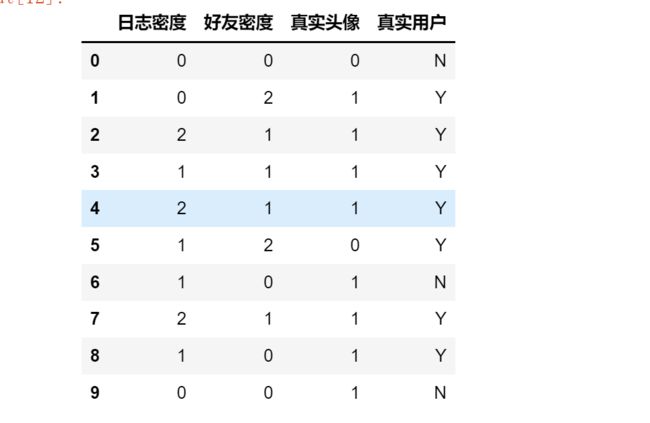
X数据说明:
X中的特征表示,社交软件上,日志的多少,好友的多少,以及是否使用真实头像,进而判断是否是真实用户,y表示是否是真实用户。
这里进行模型的预测之前,需要将数据X中的srt类型的字符变为数字才能进行计算
# 此时需要将上面的X和y的值都变为数值,因为不能计算str类型的字符
# 此时使用DataFrame中的方法,map,或者是applymap
# X = X.applymap({'s':0,'m':1,'l':2,'N':0,'Y':1})
X['日志密度'] = X['日志密度'].map({'s':0,'m':1,'l':2})
X['好友密度'] = X['好友密度'].map({'s':0,'m':1,'l':2})
X['真实头像'] = X['真实头像'].map({'N':0,'Y':1})
# 这里只能执行一次,再次再次执行的话,会再次进行替换,但是里面没有文本,最终都会是NaN1.2决策树创建和可视化
model = DecisionTreeClassifier(criterion='entropy')
# entropy表示交叉熵,用以判定分类条件,这里还可以选择gini 系数
model.fit(X,y)
# 决策树可视化
fn = X.columns
dot_data = tree.export_graphviz(model,filled=True,feature_names=fn)
# 将通过tree.export_graphviz得到的节点数据进行存储
graph = graphviz.Source(dot_data)
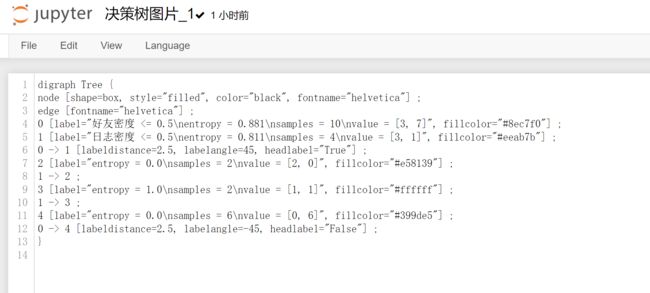
graph.render('./决策树图片_1',format = 'png')# 进行图片保存
这里使用graphviz这个包进行可视化,看起来比使用tree.plot_tree()更美观,
得到的图片因为字体的原因无法显示中文。此时可以更改上面决策树可视化中创建的dot_data,这是决策树节点文件,在生成决策树图片时会一起生成,名称与决策树图片名一致,位置在当前文件夹:
(文件内的内容)
解决:
#替换文中的fontname,替换成中文字体,这里替换为FangSong,中文仿宋
firm = open('./决策树图片_1','r',encoding='utf-8')
with open('./决策树图片_2','w',encoding='utf-8') as f:
s = re.sub(r'fontname="helvetica"','fontname="FangSong"',firm.read())# 注意文本需要跟原文一致(双引号)
f.write(s)
firm.close()graph = graphviz.Source.from_file('./决策树图片_2')
graph.render('./决策树图片_2',format = 'png')2.手动计算最佳分裂条件
主要原理:
1.计算未分裂是y的熵,也就表明初始y中信息的混乱程度;
2.计算分裂条件,根据X[i]的不同分裂条件计算y的信息熵,与未分裂时的熵作比较,信息增益大的为分裂条件
信息熵的公式:
信息增益是知道了某个条件后,事件的不确定性下降的程度。写作 g(X,Y)。它的计算方式为熵减去条件熵,如下:
(1)获取y中数值的概率
p1 = (y=='Y').mean()
p2 = (y=='N').mean()
display(p1,p2)接着,求此时(未分裂时)y的信息熵
# 计算出未分裂时的熵
p = p1*np.log2(1/p1) + p2*np.log2(1/p2)
p此时计算出entropy
(2)接着,我们需要计算H(Y|X),也就是在X的条件下的y的熵,因为这里有三个特征,需要分别计算其H(Y|X)并比较谁更小,更小表示这一特征提供的信息量大,可以作为第一次分列的主要特征。
进行计算之前,我们先将y合并到X中,便于进行操作。
X['真实用户'] = y
Xlow_entropy = 1
best_split = {}
for i in range(3):
# 取出对应特征列
# print(a)
col = (X.columns)[i]# 列名
a = X[col]
s = a.unique()
s.sort()
s = X['好友密度'].unique()
s.sort() # 排序,属性值,0,1,2
print(s)
for j in range(len(s)-1):
split_cond = s[j:j+2].mean()
cond = X['好友密度']<=split_cond# 将X分为左右两边,里面也是True和False的数据
p = cond.value_counts()/cond.size# 里面包含着True和False的概率
# print('p的值',p)
indexs = p.index
entropy = 0
for index in indexs:# 根据值得不同,分为左边True和右边False
user = X[cond==index]['真实用户']
user_p = user.value_counts()/user.size#一边中的两种情况
entropy += (user_p*np.log2(1/user_p)).sum()*p[index]
# 将得到的entropy记录下,获取最优的entropy
print('------------',p[index],(user_p * np.log2(1/user_p)).sum())
if entropy最终结果表示,使用第二列(好友密度),最佳分列条件为0.5可以使得信息增益最大。符合可视化的中展现的结果。