数据分析-深度学习 Day1

目录：

第一节 机器学习&深度学习介绍

第二节 机器学习攻略

一、机器学习的框架

二、模型训练攻略

三、针对Optimization Issue的优化，类神经网络训练不起来怎么办

(一) 局部最优点和鞍点

(二) 批处理和momentum

(三) 自动调节学习率Learning rate

(四) 损失函数带来的影响

待更新.......

本节主要介绍机器学习的框架以及模型训练的攻略

一、机器学习的框架

给定一个数据集， {(x1,y^1),(x2,y^2),...,(xN,y^N)} ，模型训练过程如下：

Step1：定义一个未知参数的函数（也就是设计一个模型） y=fθ(x)
Step2：定义一个基于训练数据的损失函数 L(θ)
Step3：优化模型参数 θ∗=argminθL

最后就是在测试集上进行模型效果测试。整个过程可以说是非常简单，基于本人从事ML的一些经验来看，主要的难点在于下面一些，仅供参考：

1、特定任务的模型设计，即如何设计一个较优的假设空间。
2、如何充分利用数据，即如何使经验风险最优化更接近于期望风险最优化，也就是数据更接近于真实数据分布。
3、如何优化模型参数，即如何让模型在训练的过程中找到全局最优解。

二、模型训练攻略

这一部分主要是讲，在一些实践工程中如何更好地让机器学习到一个比较好的model，在遇到一些问题时我们又该如何解决？李宏毅老师从直观的损失函数做分析，做了以下总结，这也是本人在实际过程中会采取的一些思考方法。

假如我们在训练一个model的过程中，当训练结束之后，发现在test集上效果不是很好，我们首先要做的检查我们的training loss，如下图所示，可以分以下两种情况讨论：

1. training loss比较大，这个时候显然说明模型在训练集上就没有学好，这个时候可以是由以下两种可能所引起：

Model bias 模型本身带来的偏差，即模型过于简单，也就是说在已知设定的假设空间内，不管怎么训练都无法找到某一个假设使得模型很好的拟合训练数据，这个时候应当增加模型的复杂性，让模型更复杂一些，比如添加更多的特征、添加更多的网络层，选择一个更复杂的model等等。

Optimization Issue 模型没有调优至最佳，原因是在训练过程中模型陷入局部最优，也就是说在现有的假设空间内算法调优不仅没有找到最优解，而且差的有点多，现有调优算法无法跳出局部最优。

这种情况下，如何区分Model bias问题还是Optimization Issue问题呢？

答案是可以尝试在现有模型上先增加模型的复杂度，比如多一些层等等，然后看看加了模型复杂度之后，模型在训练集上的training loss是不是有所下降。如果下降了，说明是Model bias，但是如果training loss不降或者反而升上去了则说明是Optimization Issue，就如下面一张这张表格，1~4层training loss都在降低，说明是Model bias问题，但是到第五层training loss上去了，说明是Optimization Issue，也可以认为是Over fitting。

2. training loss比较大，但是testing loss比较大，显然说明模型在训练集上拟合的很好，但是在测试集上偏差很大，可能的原因有以下两个：

Overfitting 最简单的解决方法就是增加训练数据、数据增强，其次就是给与模型一些限制，缩小假设空间，比如更少的模型参数、减少特征数量、参数共用、正则、Dropout、Early stopping等等，但如果限制太强，会是的模型复杂度降低或者模型没有训练完，这导致的结果就是回到了前面的model bias的问题。

Mismatch 这种情况产生原因是训练集的数据分布和测试集的数据分布不一样导致，如果实际过程中遇到这种情况，就调整我们的训练集和测试集即可，这要在一开始准备数据的时候就要避免的问题，所以后面我们不对这类问题做过多的讨论和分析，如果遇到，就只能从数据层面入手。

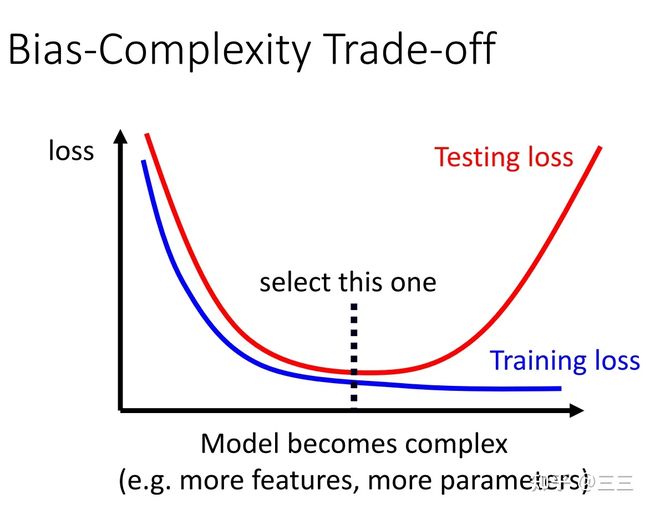
那针对Overfitting的情况，这个时候我们可以通过查看training loss和testing loss随模型复杂度变化的曲线图（不过实际过程中会先看training loss和testing loss随训练步骤变化的曲线图）来避免陷入model bias。

通常按照上图所示的最佳点找到最优的模型，是能够在测试集和训练集上都表现的很好的，但如果我们只把数据分成一份测试集和一份训练集，依旧可能会出现过拟合的现象，原因是我们在模型调优的过程中，一直在使用这份测试集做为标准在测试调优，导致最后在经过多轮调优之后，模型在测试集和训练集上都拟合的很好，loss都很低，那这个时候怎么办呢，这个时候我们需要一个private testing set（注意这个private测试集我们不用它来进行调优，只是用作测试），同时我们有一个validation data，并且这个validation data是从我们的训练集中划分出来的作为测试调优的验证集，也可以用Cross Validation的方法做验证，以防止模型过拟合。

三、针对Optimization Issue的优化，类神经网络训练不起来怎么办

所谓的模型训练不起来，顾名思义是说，在模型训练的过程中，当模型训练到一定程度之后，training set 的loss在达到了一个比较稳定的值，要么这个值从一开始就维持在一个比较大的水平，要么就是这个值下降到某一个值就不在继续下降，但显然没有达到很小。

(一) 局部最优点和鞍点

上述这种情况，说明训练到一定程度，损失函数的梯度已经接近于0了，但是接近于0有两种可能，一种是梯度更新到了局部最优点（local minima），另一种是梯度更新到了一个鞍点（saddle point）。

想要知道梯度更新之后损失函数到达的是哪个点，就需要知道当前的损失函数具体长什么样子，假设已经训练好了一组参数 θ=θ′ ，那么在 θ′ 附近的函数表达式，我们可以通过二阶泰勒展开得到：

L(θ)≃L(θ′)+(θ−θ′)Tg+12(θ−θ′)TH(θ′−θ′)

公式中的 g 和 H 分别是 L 关于 θ 的一阶和二阶微分， H 也被称为Hessian matrix，当模型训练达到局部最优或鞍点时， g=0 ，此时

L(θ)≃L(θ′)+12(θ−θ′)TH(θ′−θ′)=L(θ′)+12vTHv

观察上式，当对于所有的 v ：

vTHv>0 时，即对于 θ′ 附近所有的 θ ，都有 L(θ)>L(θ′) ，即 H 矩阵的所有特征值为正，说明此时该点为局部最小点

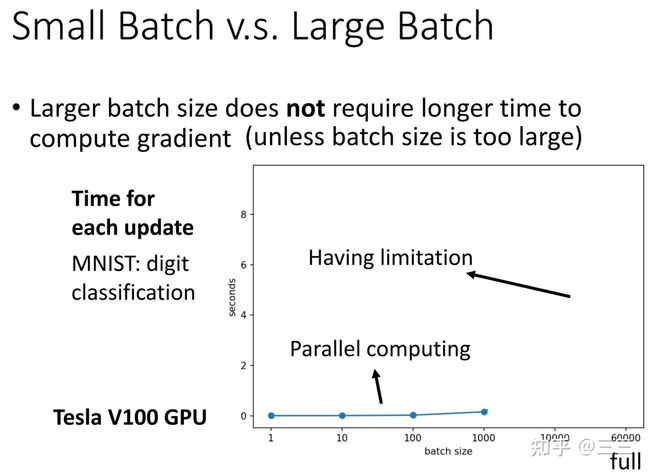
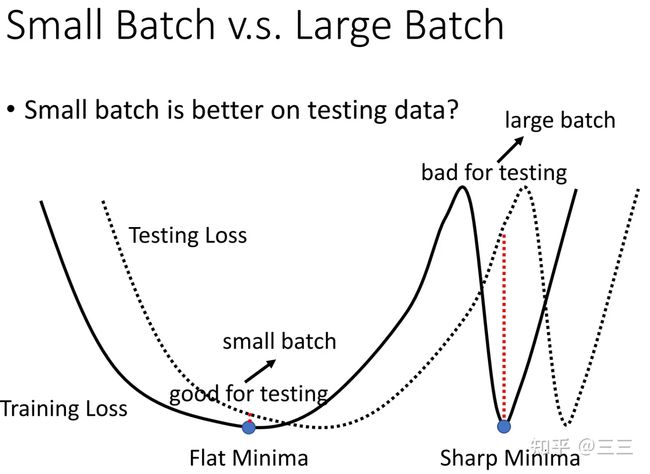
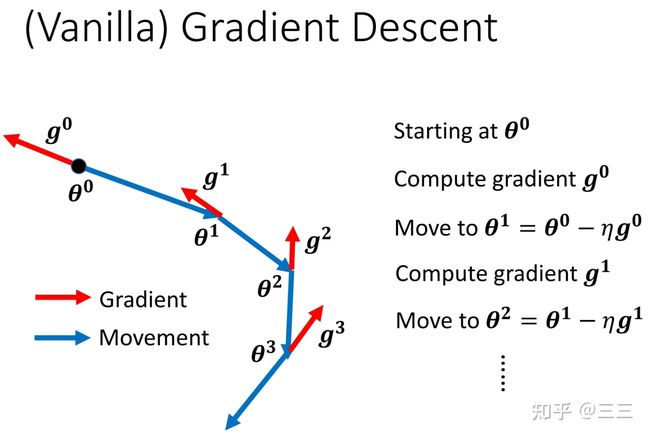
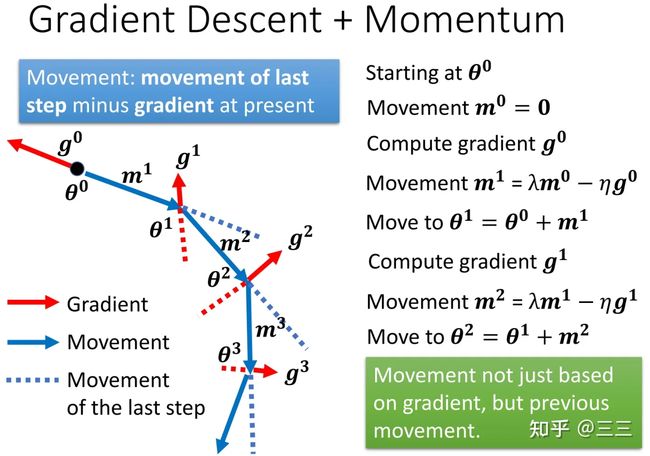
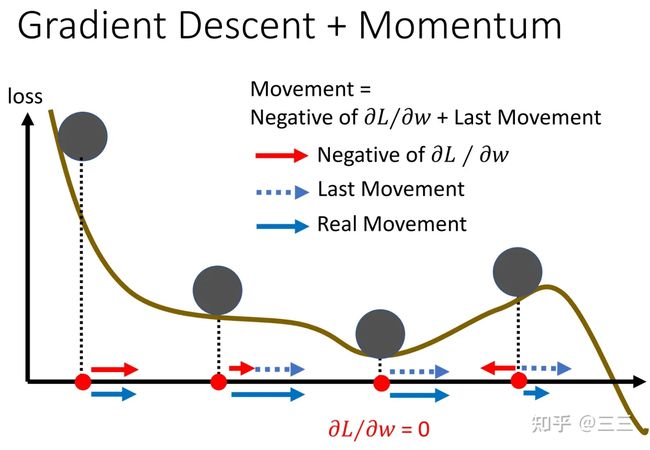
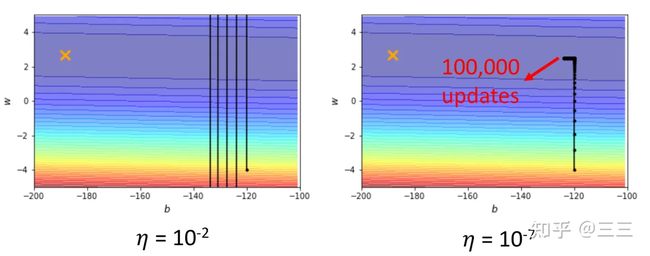
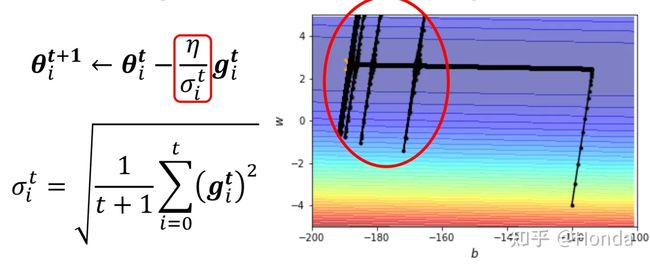
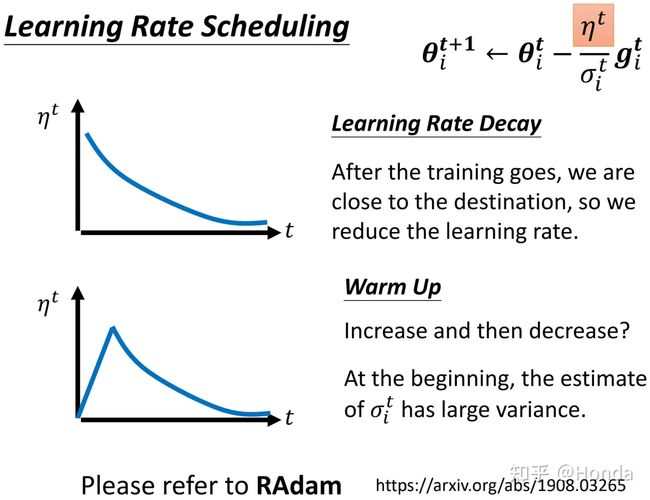
vTHv<0 时，即对于 θ′ 附近所有的 θ ，都有 L(θ)

有的点 vTHv>0 ，有的点 vTHv<0 时，即对于 θ′ 附近的 θ ，有 L(θ)>L(θ′) ，也有 L(θ)

Hessian矩阵不仅可以用于判断当前优化的点是局部最优点还是鞍点，同时，假设即便我们知道了该点为鞍点，我们依旧可以得知梯度更新的方向及大小，具体推导如下：

假设已知 u 为 H 的一个特征向量， λ 为特征向量 u 对应的特征值，且 λ<0 那么有：

uTHu=uTλu=λ‖u‖2<0

此时如果我们取 θ−θ′=u ，则有 L(θ)≃L(θ′)+12uTHu ，又由于 uTHu<0 ，所以 L(θ)

讲到这里，其实关于局部最优和鞍点的判断就差不多了，但是李宏毅老师在最后又讲了一个非常有用的经验，就是实际过程中，我们并没有必要去纠结模型到底学到了局部最优点还是鞍点，由于我们的网络处在一个非常高的高维空间中，而在高维空间中，局部最优点并不常见，多数情况下，当我们训练到一定阶段，发现gradient很小，往往是因为卡在了一个鞍点。

(二) 批处理和momentum

前一节我们讲了关于局部最优点和鞍点的判断方法，以及对于鞍点如何进行梯度更新，这一节讲讲在模型训练过程中的技巧，如何更好的学习模型，防止模型陷入”坏的”局部最优点或者鞍点。

第一个技巧：批处理（Batch）

通常情况下，我们会将 L 个训练样本分成 N 份（分之前，通常需要对这些样本进行随机打乱shuffle），并且每份的大小为batch个，当然最后一份可能会比batch少，然后模型在训练的时候，每次都是用batch个样本进行梯度更新（update），当遍历完N 个batch之后，一个epoch就训练结束了，当一个epoch结束之后，我们需要重新将这 L 个数据随机打乱，然后再次分成 N 份，再进行训练梯度更新，循环往复，直到训练完设定好的epoch数之后，训练结束，具体流程如下图所示，（ppt中最后两个式子有误，应该是g2）

想象一下，假如我们在训练过程中没训练一个样本（对应batch比较小的情况），就做一次梯度更新，很显然，由于每次更新梯度多数情况下是不一样的，当遍历完所有 L 个样本之后（一个epoch之后）会看到一条比较杂乱无章的曲线，也就是梯度更新“走的路程”会比较多，也比较乱。而当我们每次训练的时候拿所有的样本进行一次梯度更新的时候（对应batch比较大的情况），这个时候，我们会发现梯度更新只有一次，也就只“沿梯度方向走了一下”，因此会看到一条比较直的曲线。

这两种方式各有优劣，当取batch比较大的时候，模型更新一次梯度的时间会比较长（通常情况下这个batch只有当取非常大，大过上千个样本的时候，才会有明显的时间差异，后面有说明），因为实际运算的时候，GPU可以并行计算梯度），但是每次梯度更新相对来说比较稳，梯度更新的方向比较准确，起伏不会太大，而当取batch比较小的时候，模型更新一次梯度的时间虽然比较短，但是每次梯度更新会存在noisy，或者说梯度更新的方向不太准确，如下图所示：

两点说明：

1、Large Batch并不一定在每一次训练一个batch的时间上大于Small Batch，通常情况下只有当Large Batch非常大的时候（超过几千），两者才会有明显的时间差，这得益于每一次梯度更新运算GPU都是并行计算梯度，下面这个例子就能说明当batch大于1000之后才会有明显的时间上的差异，当batch=60000的时候，实际也就只花了10s的时间，也是相当快的，

2、前面已经说了，batch=1和batch=1000，GPU运算所消耗的时间几乎差不多，然而，假设我们的训练样本 L=60000 个，当batch=1的时候，每一轮epoch需要训练要耗费60000*1=60000s，当batch=1000是，每一轮epoch只需要耗费60000/1000=60s就可以了，也就是每一个epoch训练所需的时间反而更短，这个时间就很显而易见了，因此通过时间这个维度来比较小batch和大batch之间的差别，显然不够精确。也就是说通常情况下，大batch训练在有GPU运算的时候所需时间反而更短。

3、那前面这两点是不是就说，大的batch size就一定好了呢，前面说了，大的batch size梯度在更新的时候会更稳，且更新的时候更能精准的沿着梯度下降的方向做梯度更新。然而，实验证明，小的batch size反而更有助于模型训练，下面两张图是模型训练精度和batch size大小的关系图，当batch size过分大的时候（大过几千），模型的精度会有明显的下降，这个现象不是Overfitting，也不是Model bias造成的，而是Optimization造成的。

为什么会这样呢？（小的batch要比大的batch好）

声明：这里包括前面所说的大batch，是很大的batch，通常是过千个样本，或者是整个数据集，而不是256、128和64之间的大小差异，后面的解释我们都规定大的batch size为整个training data

一个可能的解释是，当采用大batch size训练时，并且当参数更新至局部最优点或者鞍点的时候，显然梯度为0，就不会再更新了，因为下一次更新时输入数据没有改变，损失函数也不会有变化，但是，如果现在是将一小部分数据作为一个batch进行训练，每次训练时batch里面的数据都是不一样的（这也是为什么每个epoch都要将数据shuffle的原因），那在每一次做training update的时候，会得到不一样的梯度，损失函数在某个batch数据上关于参数 θ 的梯度为0，这个时候在这个batch上不会更新梯度，但是，在另外一个batch上，损失函数关于参数 θ 的梯度不一定为0，因为输入变了，损失函数也变了。

另外一种解释是，在大batch数据上训练容易造成过拟合，所谓过拟合意思是说，当我们使用大batch size做training和小batch size做training，并同时让它们在training data上达到一样的accuracy，此时在小batch size上训练得到的model在testing data上的accuracy要高于在大batch size上训练得到的model在testing data上的accuracy，也就是说小batch size上训练得到的model泛化性更好。这里李宏毅老师引用了一篇paper里的解释来说明是由于在大batch size上training的到的model更容易陷入”坏的“local minima，不容易跳出局部最优，因此它针对的是整个数据集上的梯度更新策略，如果模型陷入了”坏的“local minima，那么这个时候的损失函数只是适应了当前数据的梯度方向为0，而对于新的数据（比如testing data）也许在这个位置的梯度不一定为0，也就是说在testing data上损失还很大。假如我们现在采取的是小batch size做training的话，同样是陷入local minima，这个虽然也是局部最优，但是由于此时的损失函数是相对于很多个不同batch的数据在该点梯度方向都为0，也就是说有很强的泛化性，这就很有可能使得训练好的model在testing data也有较好的表现。

下面一张图是关于小batch size和大batch size的一个总结：

第二个技巧：动量（Momentum）

所谓的动量就是在梯度更新的时候，人为的给与某个方向上的梯度，使得当损失函数到达局部最优的时候，有能力能跳出这个局部最优值。就像下面那个小球一样，当模型训练到达从左往右第四个小球的位置的时候，Loss关于w的一阶梯度为0，如果这个时候人为的给与某个方向上的”动量“，就能使小球逃离这个局部最优点。（这就有引出两个疑问 1、动量的方向，2、动量的大小）

我们先来看下一般情况下的梯度下降法，下面这张图显示，可以看到每一次参数更新都是朝着Gradient的反方向去更新，梯度更新规则如下：

θt=θt−1−ηgt−1

加入Momentum技术后的Gradient descent方法，每一次在更新参数的时候，更新的方向是当前梯度的反方向（ −g ）加上前一步参数更新的方向（ m ， m 的初始值为0），也就是说参数更新的方向不只是取决于当前梯度的方向，还取决于过去的参数更新方向。迭代公式如下所示，式子中我们可以认为 mt−1 代表了过去时刻梯度的总和（注意：Momentum会考虑梯度的方向）， gt−1 则代表了当前时刻的梯度，而 λ 和 η 则分别代表了过去时刻和当前时刻梯度的权重

mt=λmt−1−ηgt−1θt=θt−1+mt

这样的话，假设当前梯度已经为0了，也就是到了局部最优的点，但是由于前一次梯度一定不为0，m大概率不会等于0，那即使是在局部最优的点，也会存在有动力可以跳出这个局部最优的点，当然如果这个局部最优的点是一个比较好的点，附近所有的点的梯度都很小的时候，就不容易跳出，因为这个时候前期积累的能量 m 不会太大，可以想象小球在该点来回摆动多次之后最终到达平衡点，当然这个时候我们也认为这个点并不是一个“坏的”局部最优点（类似于前面图中那张口子比较大的那个局部最优点），而当这个点是一个比较陡峭的局部最优点的时候，就比较容易跳出这个点，这就是为什么Momentum能防止过拟合的原因。

(三) 自动调节学习率Learning rate

前面两节讲到，当model在训练过程中，发现training loss不再下降的时候，就是损失函数的gradient很小了，或者说几乎等于0，陷入局部最优或者鞍点。真的是这样子的吗？

其实，我们可以从梯度更新的式子中可以发现： θ→θ+ηg ，式子中还有一个参数 η 学习率，假如模型训练至某一时刻，发现training loss不再下降，除了因为gradient很小，还有一种可能就是此时的学习率 η 已经很小了。

这里，李宏毅老师又放了一个干货，之前我一直以为，training loss不再下降的时候，多数情况下是陷入了局部最优，但李宏毅老师在课程中说，其实想让一个model陷入局部最优是很难的，也就是说让gradient等于0这件事通常不会发生，我们可以看下面两张图，这两张图中可以发现，当我们的学习率比较大 η=10−2 的时候，梯度更新很离谱，几乎不会走到最优点（打叉的那个点），而当 η=10−7 比较小的时候，训练了100000多步都不能收敛到局部最优点，原因是当training到后面的时候，学习率已经非常小了，这个时候梯度不起作用了。

那如何定制化我们的学习率，使得它能够适应当前的梯度，并用较少的training step就能到达最优点呢？

一种想法就是，

敲黑板：当当前方向的梯度比较大的时候，给与较小的学习率，当当前梯度较小的时候，给与较大的学习率（这段话我认为是所有优化算法的核心思想）

假设我们当前需要更新第 i 个参数 θi 在 t+1 时刻的梯度时，那更新的方式如下所示：

θit+1=θit−ηgitgit=∂L∂θi

而如果想要达到定制化学习率，就需要对学习率进行改动，改动的方式就是给每个 t 时刻的θi 的学习率设定一个系数 σit ，于是，梯度更新变成如下所示：

θit+1=θit−ησitgit

也就是说，不同的参数就有不同的学习率，相互之间是独立不影响的，同时不同的迭代周期对于同一个参数下也会有不同的学习率，接下来我们看看，有什么样的方式可以做到这样子？

敲黑板：所有的优化算法都是基于上面这个公式在做更新优化，主要的更新对象就是 η 和 σit ，以及 git 梯度本身的改动，就这三个变量，所有优化算法都是围绕这三个变量在变来变去

第一种：对 σ 的改进

方法一：Root Mean Square(平方根)

具体流程如下所示（太多了，就不全打下来了...），主要的更新规则是当前参数θi在 t 时刻学习率参数系数 σit 和 t 时刻（当前）以及之前（过去）（注意：Root Mean Square只考虑过去梯度的大小，不考虑方向）损失函数关于 θi 的梯度的平方和有关

σit=1t+1∑i=0t(git)2

其实熟悉的同学一眼就能看出，这一招就是被用在Adagrad优化算法中，从算法中我们可以发现， σit 和gradient的平方和是成正比的，所以学习率和gradient的平方和成反比，因此，如下图所示，当我们遇到一个比较平稳的局部最优区域时（蓝色曲线），此时该点附近的大部分区域梯度都很小，这个时候就可以给与一个较大的学习率，反之如果遇到的是一个比较陡峭的局部最优区域（绿色曲线），此时该点附近的大部分区域梯度相对来说都比较大，这个时候就需要一个比较小的学习率，让参数更新慢一些。但细心的同学也许会发现，Adagrad并没有对当前时刻的梯度和过去时刻的梯度给与不一样的权重考虑，因此Adagrad算法势必存在一些问题，下面我们来分析下。

方法二：自适应学习率（RMSProp）

Adagrad算法其实还有一个缺陷，那就是在实际工程中，我们并不会经常遇到像上图展示的那两张图那样，具有那么平滑的局部区域，通常情况下，局部最优区域是有平滑部分也有陡峭部分，而不是像上面抛物线那样这么平滑，那这个时候，我们通常需要学习率可以自适应，也就说，当它走到坡度比较小的地方，学习率就不要太小，当坡度比较大的时候，学习率不要太大，RMSProp给出的 σit 更新策略如下所示，我们可以认为 σit−1 代表了过去时刻的gradient，而 git 则代表了当前时刻的gradient，想象一下，假如当前走到了一个比较陡的坡度，那显然，我们希望当前的gradient影响不要太大，此时的 α 会比较大，反之α 就比较小

σit=α(σit−1)2+(1−α)(git)2, σi0=(gi0)2=|gi0|, 0<α<1

方法三：Adam = RMSProp + Momentum

我们先来总结一下Momentum和RMSProp这两个优化算法，Momentum的目的是防止陷入局部最优，当梯度更新陷入局部最优或者鞍点时，Momentum可以为梯度更新提供新的“动力”，而这个动力和最优点附近的梯度有关，也就是说Momentum是对梯度（ g ）本身的改进优化，RMSProp的目的则是自适应的调整学习率，使得模型能够快速并且稳定的到达最优点，RMSProp是对学习率系数（ σ ）的改进和优化，Adam则同时对 g,σ 两个参数做改动，更新规则如下：

mt=β1mt−1−(1−β1)g′t−1vt=β2vt−1−(1−β2)g″t−1θt=θt−1−ηvt+εmt

其中 g′ 是一阶梯度，g″ 是二阶梯度，关于一阶梯度对梯度更新的影响不再赘述，可以参考前面的Momentum思想，Adam算法对于 σ 的改进采用了二阶梯度，Momentum的思想是我们可以慢慢多走几步，就能根据坡度的变化直接调整。现在如果能用二阶梯度，相当于梯度的梯度，那么也就知道坡度变化的趋势，因此一步就能走到位。所以二阶梯度本质上比一阶梯度多出一些信息，模型收敛也就会更快。下图中蓝色曲线是利用一阶梯度信息更新，红色曲线是二阶梯度信息更新，可以明显看到，红色曲线收敛更快。

第二种：对 η 的改进

方法一：learning rate decay

下面一张图展示了当给定学习率 η ，并采用Momentum技术做优化的时候，当training到一定的step，会有突然向两边偏离的现象，这种现象产生的原因是因为在发生这种偏离之前，梯度虽然很小，但是有积累，随着 t 的不断增大， σ 在减少，此时 η/σ 反而变大，就会发生突然偏离”航线“的状况，当然，训练一定step之后，还是会走到局部最优点。

因此，如果想要曲线收敛的更平稳，需要对 η 也要做一定的限制，比如，越到后面 σ 在减小，此时相应的η 也要减小，这就是学习率衰减，通常在我们的实际工程中就是给定一个学习率衰减系数，比如常见的指数型衰退法，式中的 α 为衰减系数， decaysetp 代表了每多少步衰减一次，

ηt=ηt−1∗αglobalstep/decaysteps

这个时候的 η 就变成了一个和时间有关的变量，最终训练的步骤呈现下面ppt中右边的形式。

方法二：warm up

前面学习率衰减的方法，学习率随时间是一直在衰减的，但是warm up的策略则是让学习率 η 先增大，后减小，为什么warm up会有效果呢？李宏毅老师给出了一个可能的解释是：在模型刚开始训练的时候，每个数据点对模型来说都是新的，并没有学到任何东西，或者说并不知晓数据的分布情况，这个时候的 σ 统计是不精准的，模型这个时候如果给与比较大的学习率很容易学偏，并且在一开始的时候很难把错误的点拉回来，因此在模型一开始训练的时候让它慢慢学，等到学到一定的先验知识，对数据分布有了解之后，再加大学习率去学习，至于后面为什么要小下去，这个解释和前面的learning rate decay的思想一样。

关于warm up的一些其他版本的理论解释，推荐一篇博文，供大家学习参考，个人觉得解释的也蛮清楚的。这篇博文总结下来有两点（好吧，其实我觉得是一个意思...[狗头]）：

1、通常情况下，mini-batch扩大k倍，学习率也可以扩大k倍，但这种情况，仅仅适用于数据量较小，并且每个batch分布比较近似的情况。

2、warm up这种技术对于大网络和大数据集会比较适合，理由是，数据集越大，每个mini batch的variance就越大，越大的学习率越容易在前期学偏，陷入“过拟合”

神经网络中 warmup 策略为什么有效；有什么理论解释么？1552 关注 · 15 回答问题

总结：

上面所有方法都可以用一个式子做总结：θit+1=θit−ηtσitmit

式子里的各个参数就不重复介绍了，前面应该讲的很清楚了，所有的优化算法都是围绕这个式子做的优化。

(四) 损失函数带来的影响

开门见山，前面讲的是如何让模型参数训练地更快、更稳，这些方法适用于任何损失函数，但是，如果在模型训练一开始，就给与一个比较容易训练的损失函数，或者说比较平滑的损失函数，没有太多locla minima的损失函数，是不是就更容易training了呢？

这部分在李宏毅老师的课程中举了Cross-entropy和MSE这两个loss的，具体可以看下面一张图，Cross-entropy的损失函数曲面梯度变化比较平稳，而MSE在损失比较大的地方，梯度基本不变化，这个时候就很难用梯度下降去更新参数了。