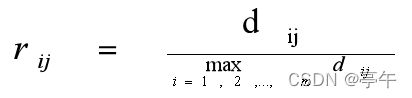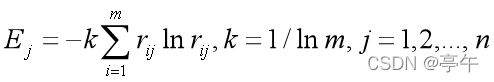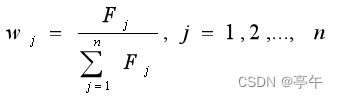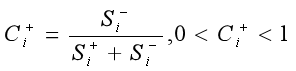离散模型——多属性决策

数学模型 7.1 P233

目录

多属性决策

定义：

第一步：确定决策矩阵并标准化

1）确定决策矩阵：

2）决策矩阵标准化：

第二步：确定属性权重

 第三步：综合方法

1）将决策矩阵模一化后的rij×属性权重wj，构成矩阵V

2）取出正理想解（由每列向量中最大元素构成），记为v+

            负理想解（由每列向量中最小元素构成），记为v-

3）计算方案Ai与正、负理想解的欧式距离：

 4）定义方案Ai与正理想解的相对接近度

---

多属性决策

定义：

方案的优劣由若干属性（如汽车的价格、性能、款式等因素）给以定量或定性的表述，而人们在若干备选方案中选出最优方案，或者对这些方案按照优劣程度排序，或者需要给出优劣程度的数量结果。

第一步：确定决策矩阵并标准化

1）确定决策矩阵：

一个多属性决策问题有m个备选方案A1,A2,…,Am，n个属性X1,X2,...Xn，方案Ai对属性Xj的取值为dij。D=(dij)m*n称为原始决策矩阵。

汽车型号\属性	X1价格（万元）	X2性能（满分10分）	X3款式（满分10分）
A1	25	9	7
A2	18	7	7
A3	12	5	5

决策矩阵的获取有两种方法。

一种偏客观，直接通过量测或调查（偏客观）；一种偏主观，由决策者或请专家评定。

2）决策矩阵标准化：

由于通常各属性物理意义各不相同，在下一步分析前需将原始决策矩阵标准化。

首先，将各属性区分为效益型属性和费用性属性。

效益型属性：属性值越大，该属性对决策的重要程度越高。

费用型属性：属性值越大，该属性对决策的重要程度越小。

通常对费用性属性作变换，取原属性值的倒数，将全部属性统一为效益型。

 之后，对原始决策矩阵D标准化，将标准化的决策矩阵定义为R。

标准化有以下三种方法：

归一化，R的列向量分量之和为1：

最大化，R的列向量最大值为1：

模一化，R的列向量的模为1：

clc,clear
d=[25 9 7;    %每行为一个方案，每列为一种属性
   18 7 7;
   12 5 5];
%% 原始决策矩阵标准化
l=1;             %费用型属性
d(:,l)=1./d(:,l);%将费用型属性变换为效益型
%归一化
r=d./sum(d,1);         %sum函数参数2表示按照每列相加
%最大化
%r=d./max(d,[],1);     %max函数参数3表示取每列的最大值
%模一化
%r=d./sum(d.^2,1).^0.5; %sum函数参数2表示按照每列相加

第二步：确定属性权重

信息熵法：一个信息量的（概率）分布越趋向一致，所提供信息的不确定越大，用熵作为衡量不确定的指标。在多属性决策中，将标准化决策矩阵R的各个列向量看作每个属性信息量的概率分布。按照Shannon对熵的定义，各方案关于属性Xj的熵为

熵值越大，代表信息不确定性越大（信息量概率分布越趋向一致），属性Xj对于辨别方案优劣的作用越小。

定义

 为属性Xj的区分度。（Fj越大，Xj的区分度越大，属性Xj越重要）

将归一化的区分度取作属性Xj的权重wj，即

d=[25 9 7;    %每行为一个方案，每列为一种属性
   18 7 7;
   12 5 5];
m=size(d,1);  %m种方案
n=size(d,2);  %n种属性
%% 属性权重的确定
E=(-1/log(m))*sum(r.*log(r),1);  %E熵值，sum函数参数2表示按照每列相加
F=1-E;                           %F区分度
w=F/sum(F);                      %w各属性的权重

 第三步：综合方法

确定最优方案，或者各方案按照优劣排序的数量结果。

这里使用topsis法（接近理想解的偏好排序法）来对方案排序。

理论上的最优方案（称正理想解）由所有可能的加权最优属性值构成，最劣方案（称负理想解）由可能的加权最劣属性值构成。定义距正理想解尽可能近、距负理想解尽可能远的数量指标——相对接近度，备选方案的优劣顺序按照相对接近度的大小确定。

1）将决策矩阵模一化后的rij×属性权重wj，构成矩阵V

（注意：这里用模一化的决策矩阵，以便在空间定义欧氏距离，但属性权重w中仍可使用归一化方法处理决策矩阵）

2）取出正理想解（由每列向量中最大元素构成），记为v+

            负理想解（由每列向量中最小元素构成），记为v-

V_max=max(V,[],1);       %正理想解，max函数参数3表示取每列的最大值
V_min=min(V,[],1);       %负理想解，min函数参数3表示取每列的最小值

3）计算方案Ai与正理想解的欧式距离：

与负理想解的欧式距离 ：

S_plus=sum((V-V_max).^2,2).^0.5;    %求各方案与正理想解的欧式距离，sum函数参数2表示按照每行相加
S_minus=sum((V-V_min).^2,2).^0.5;   %求各方案与正理想解的欧式距离，sum函数参数2表示按照每行相加

 4）定义方案Ai与正理想解的相对接近度为

之后对进行归一化处理，越大，表示方案越好。

C=S_minus./(S_plus+S_minus);        %C，各方案与正理想解的相对接近度
C=C./sum(C,1);                      %C归一化处理
[Y,index]=sort(C,1,'descend');       %参数2按列排序，参数3降序，Y排序后的结果，对应index原矩阵下标

 完整代码如下：

clc,clear
d=[25 9 7;    %每行为一个方案，每列为一种属性
   18 7 7;
   12 5 5];
m=size(d,1);  %m种方案
n=size(d,2);  %n种属性
%% 原始决策矩阵标准化
l=1;             %费用型属性
d(:,l)=1./d(:,l);%将费用型属性变换为效益型
%归一化
r=d./sum(d,1);         %sum函数参数2表示按照每列相加
%最大化
%r=d./max(d,[],1);     %max函数参数3表示取每列的最大值
%模一化
rm=d./sum(d.^2,1).^0.5; %sum函数参数2表示按照每列相加
%% 属性权重的确定
E=(-1/log(m))*sum(r.*log(r),1);  %E熵值，sum函数参数2表示按照每列相加
F=1-E;                           %F区分度
w=F/sum(F);                      %w各属性的权重
%% topsis法确定方案优劣顺序（决策矩阵需用模一化方法处理,但权重的确定仍可使用归一化等方法）
V=rm.*w;
V_max=max(V,[],1);       %正理想解，max函数参数3表示取每列的最大值
V_min=min(V,[],1);       %负理想解，min函数参数3表示取每列的最小值
S_plus=sum((V-V_max).^2,2).^0.5;    %求各方案与正理想解的欧式距离，sum函数参数2表示按照每行相加
S_minus=sum((V-V_min).^2,2).^0.5;   %求各方案与正理想解的欧式距离，sum函数参数2表示按照每行相加
C=S_minus./(S_plus+S_minus);        %C，各方案与正理想解的相对接近度
C=C./sum(C,1);                      %C归一化处理
[Y,index]=sort(C,1,'descend');       %参数2按列排序，参数3降序，Y排序后的结果，对应index原矩阵下标