pytorch梯度的计算过程

1、基础知识:

1. 与numpy中的基本操作相似， pytorch 的作用是引入GPU加快运算， 增加图形界面， 适合大数据运算， 尤其是deep learning
2. gradient 梯度类似于求导， 找到梯度下降的最佳路径。
3. tensor 除了可以进行线性代数运算， 还可以求梯度

       tensor在pytorch里面是一个n维数组。我们可以通过指定参数reuqires_grad=True来建立一个反向传播图，从而能够计算梯度。在pytorch中一般叫做dynamic computation graph(DCG)——即动态计算图。三种设置需要自动计算梯度的方式：

# 三种设置需要自动计算梯度的方式。
import torch
import numpy as np

# 方式一
x = torch.randn(2,2, requires_grad=True)

# 方式二
x = torch.autograd.Variable(torch.Tensor([2,3]), requires_grad=True)

#方式三
x = torch.tensor([2,3], requires_grad=True, dtype=torch.float64)

# 方式四
x = np.array([1,2,3] ,dtype=np.float64)
x = torch.from_numpy(x)
x.requires_grad = True
# 或者 x.requires_grad_(True)

2、举例说明梯度计算过程

1）先创建tensor变量

# Create tensors.
import torch
x = torch.tensor(3.) # 数字
w = torch.tensor(4., requires_grad=True) # 数字
b = torch.tensor(5., requires_grad=True) # 数字
x, w, b

输出结果：
(tensor(3.), tensor(4., requires_grad=True), tensor(5., requires_grad=True))

2）引入表达式y=w*x+b, y 为tensor。

# Arithmetic operations
y = w * x + b
y

输出结果:
tensor(17., grad_fn=)

3）调用backward()方法， 对y函数求导， 也就是求梯度。

# Compute derivatives
y.backward()
#相当于函数变为 y = 3 * w + b

#求梯度：
# Display gradients
print('dy/dx:', x.grad)
print('dy/dw:', w.grad)
print('dy/db:', b.grad)

输出结果：
dy/dx: None
dy/dw: tensor(3.)
dy/db: tensor(1.)

解释：对于y = x * w + b，因为x为常数3， 对y = 3 * w + b，y对x求偏导数dy/dx=0， y对w求偏导数dy/dw = 3, y对b求偏导dy/db=1.

3、举例2，说明梯度计算过程

Pytorch在梯度方面提供的功能，大多是为神经网络而设计的。而官方文档给出的定义和解释比较抽象。以下将结合实例，总结一下自己对Pytorch中梯度计算backward函数的理解。

1）简单的神经网络构建

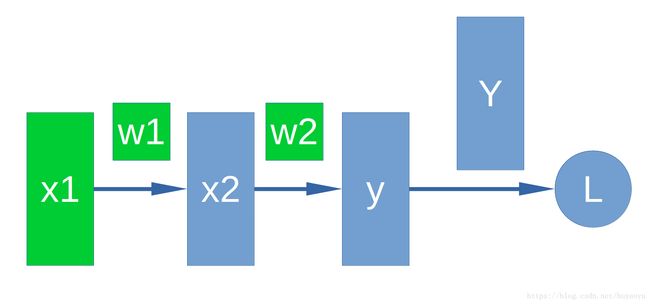
首先我们看一个非常简单的神经网络。

假设x1，x2是神经网络的中间层，y是我们的输出层，Y是真实值，L是loss。w1和w2是对应于x1和x2的weight。
上图用数学公式表示为：

• x2=w1∗x1
• y=w2∗x2
• L=Y−y

通常我们会把x1，w1，w2，x2，y使用PyTorch的Tensor进行表示。L也可以用Tensor表示(维度可能与其他Tensor不同)。
其中，我们把需要自己设定的Tensor(即不是通过其他Tensor计算得来的)叫做叶子Tensor。比如x1，w1和w2就是所谓的叶子Tensor。
在pytorch中，我们把上述模型表示出来。

import torch
import numpy as np
 
x1 = torch.from_numpy( 2*np.ones((2, 2), dtype=np.float32) )
x1.requires_grad_(True)   #设置该tensor可被记录操作用于梯度计算
w1 = torch.from_numpy( 5*np.ones((2, 2), dtype=np.float32) )
w1.requires_grad_(True)
print("x1 =", x1)
print("w1 =", w1)
 
x2 = x1 * w1
w2 = torch.from_numpy( 6*np.ones((2,2), dtype=np.float32) )
w2.requires_grad_(True)
print("x2 =", x2)
print("w2 =", w2)
 
y = x2 * w2
Y = torch.from_numpy( 10*np.ones((2,2), dtype=np.float32) )
print("y =", y)
print("Y =", Y)
 
L = Y - y

 输出结果：

x1 = tensor([[2., 2.],
        [2., 2.]], requires_grad=True)
w1 = tensor([[5., 5.],
        [5., 5.]], requires_grad=True)
x2 = tensor([[10., 10.],
        [10., 10.]], grad_fn=)
w2 = tensor([[6., 6.],
        [6., 6.]], requires_grad=True)
y = tensor([[60., 60.],
        [60., 60.]], grad_fn=)
Y = tensor([[10., 10.],
        [10., 10.]])

上述代码注意：

1. 设置一个tensor的 requires_grad为True 会保存该Tensor是否记录所有操作用于计算梯度，可直接在创建tensor时指定属性requires_grad = True，也可以使用函数x.requires_grad_(True)。
2. 通过运算得到的Tensor（非自己创建的tensor），会自动被赋值grad_fn属性。该属性表示梯度函数

2）反向传播的梯度计算

上述前向传播计算完成后，想要计算反向传播(BP)的梯度。基本原理即为求导的链式法则。上述网络的求导即为：

dL/dx1 = -1*w2*w1 = -30(tensor格式）

dL/dw1=-1*w2*x1=-12(tensor格式）

dL/dw2= -1*x2 =-10(tensor格式）

PyTorch提供了backward函数用于计算梯度 ,这一求解过程变为: 

L.backward(torch.ones(2, 2, dtype=torch.float))
print(x1.grad) # 查看L对于x1的梯度
print(w1.grad) # L对于w1的梯度
print(w2.grad)

对于最后的Tensor L执行backward()函数，会计算之前参与运算并生成当前Tensor的叶子Tensor的梯度。其梯度值会保存在叶子Tensor的.grad属性中。
比如上述网络中，x1，w1和w2就是所谓的叶子Tensor。

输出结果：

tensor([[-30., -30.],
        [-30., -30.]])
tensor([[-12., -12.],
        [-12., -12.]])
tensor([[-10., -10.],
        [-10., -10.]])

1. backward函数的gradient参数解释

gradient 在PyTorch的官方文档上解释的比较晦涩，我理解这个参数表示的是 网络的输出tensor(假设为L)对于当前调用backward()函数的Tensor(假设为Y)的导数，即gradient=∂L∂Ygradient=∂L∂Y。
(1) 比如在我上述的模型输出tensor为L，当前调用backward的tensor也为为L,则gradient表示为∂L∂L=1∂L∂L=1，也就是element全为1的Tensor。gradient维度需要 与 调用backward()函数的Tensor的维度相同。即L.backward(torch.ones(2, 2, dtype=torch.float))。
(2) 又比如，假设我们不知道L关于y的函数表示，但知道L关于y的梯度（即∂L∂y=−1∂L∂y=−1）时，我们可以在特定位置,比如中间节点y调用backward函数，通过y.backward(-1 * torch.ones(2, 2, dtype=torch.float))来完成反向计算梯度过程。 这样的设计通过链式法则，可以在特定位置求梯度值。
(3) 对于L为标量（常数）的情况，可不指定任何参数，默认参数为torch.tensor(1)。对于L为高于1维的情况，则需要明确指定backward()的第一个参数。

2. backward函数的其他注意点

(1) 默认同一个运算得到的Tensor仅能进行一次backward()。若要再次进行backward()，则要再次运算得到的Tesnor。
(2) 当多个Tensor从相同的源Tensor运算得到，这些运算得到的Tensor的backwards()方法将向源Tensor的grad属性中进行数值累加。
比如上述实例中，假设有另一个tensor L2是通过对x1的运算得到的，那么L2.backward()执行后梯度结果将累加到x1.grad中。

print("x1.grad =",x1.grad) # 原来x1的梯度 
L2 = x1 * x1
L2.backward(torch.ones(2, 2, dtype=torch.float))
print("x1.grad =", x1.grad) # 计算L2的backward后梯度结果将累加到x1.grad中

x1.grad = tensor([[-26., -26.],
        [-26., -26.]])
x1.grad = tensor([[-22., -22.],
        [-22., -22.]])

 (3) 只有叶子tensor(自己创建不是通过其他Tensor计算得来的）才能计算梯度。否则对于非叶子的x1执行L.backwar()后，x1.grad将为None。定义叶子节点时需注意要直接用torch创建且不能经过tensor计算。例如将实例中的x1定义改为x1 = 2 * torch.ones(2, 2, requires_grad=True, dtype=torch.float) 其实它已经做了tensor计算，x1将不再是叶子，表达式中torch.ones()才是叶子。

参考：Pytorch学习之梯度计算backward函数 - 亚北薯条 - 博客园

3.例子说明

import torch
a = torch.tensor([2., 3.], requires_grad=True)    
b = a + 3
c = b * b * 3
out = c.mean()
out.backward(retain_graph=True)
a.grad

结果输出：

tensor([15., 18.])

梯度推导：

 

总结：

Note1:在pytorch中，只有浮点类型的数才有梯度，故在上述方法中指定tensor的dtype类型为torch.float32类型、torch.float64、或者初始化的时候带小数点。