【推荐系统多任务学习MTL】MMoE论文精读笔记(含代码实现)
论文地址:
- Google KDD 2018 MMOE (内含论文官方讲解视频)
- PDF Modeling Task Relationships in Multi-task Learning with Multi-gate Mixture-of-Experts
一、前言
阿里团队提出 ESMM 模型利用 MTL (Multi-Task Learning) 的方法极大地提升了 CVR 预估的性能,同时解决了传统 CVR 模型预估的一些弊病。我们从模型的网络结构可以了解到,ESMM 是典型的 share-bottom 结构,即底层特征共享方式。这种 MTL 共享结构的一大特点是在任务之间都比较相似或者相关性比较大的场景下能带来很好的效果,归纳偏置的作用也能够很好的发挥出来,而对于任务间差异比较大的场景,比如建模 CTR 和观看时长,这种 MTL 共享结构就有点捉襟见肘了。
二、MMoE要解决的问题
多任务学习的本质:共享表示以及相关任务的相互影响。通常,相似的子任务也拥有比较接近的底层特征,那么在多任务学习中,他们就可以很好地进行底层特征共享;而对于不相似的子任务,他们的底层表示差异很大,在进行参数共享时很有可能会互相冲突或噪声太多,导致多任务学习的模型效果不佳。
对于相关性低的子任务。实际的应用场景中,我们可能不止有像 CTR、CVR 这样的非常相关的子任务,还会遇到子任务间关系没那么紧密的多任务学习场景,而且很多情况下,你很难判断任务在数据层面是否是相似的。所以多任务学习如何在相关性不高的任务上获得好效果是一件很有挑战性也很有实际意义的事,这也是本小节所提到的模型 “MMoE” 主要解决的问题。
MMoE 之前的解决方案。比如两个任务的参数不共用,而是对不同任务的参数增加 L2 范数的限制;或者对每个任务分别学习一套隐层然后学习所有隐层的组合。这些结构和 Shared-Bottom 结构相比,其构成的模型会针对每个任务添加更多参数以适应任务间差异,虽然能够带来一定的效果提升,但是增加了更多的参数也就意味着需要更大的数据样本来训练模型,而且这些方法会使模型变得更复杂,也不利于在真实生产环境中部署使用
MMoE(Multi-gate Mixture-of-Experts) 是 Google 在 2018 年 KDD 上发表的论文《Modeling Task Relationships in Multi-task Learning with Multi-gate Mixture-of-Experts》里提出的,它是一种新颖的的多任务学习结构。MMoE 模型刻画了任务相关性,基于共享表示来学习特定任务的函数,避免了明显增加参数的缺点。
三、MoE神经网络结构
MMoE 很重要的一步是把 MoE 引入了多任务学习中。早在 2017 年,谷歌大脑团队的两位科学家:大名鼎鼎的深度学习之父 Geoffrey Hinto 和 谷歌首席架构师 Jeff Dean 发表论文《Outrageously Large Neural Networks: The Sparsely-Gated Mixture-of-Experts Layer》 并提出了 “稀疏门控制的混合专家层”(Sparsely-Gated Mixture-of-Experts layer,MoE),这里的 MoE 是一种特殊的神经网络结构层,结合了专家系统和集成思想在里面。
MoE 由许多 “专家” 组成,每个 “专家” 都有一个简单的前馈神经网络和一个可训练的门控网络(gating network),该门控网络选择 “专家” 的一个稀疏组合来处理每个输入,它可以实现自动分配参数以捕获多个任务可共享的信息或是特定于某个任务的信息,而无需为每个任务添加很多新参数,而且网络的所有部分都可以通过反向传播一起训练。MoE 结构图如下所示:
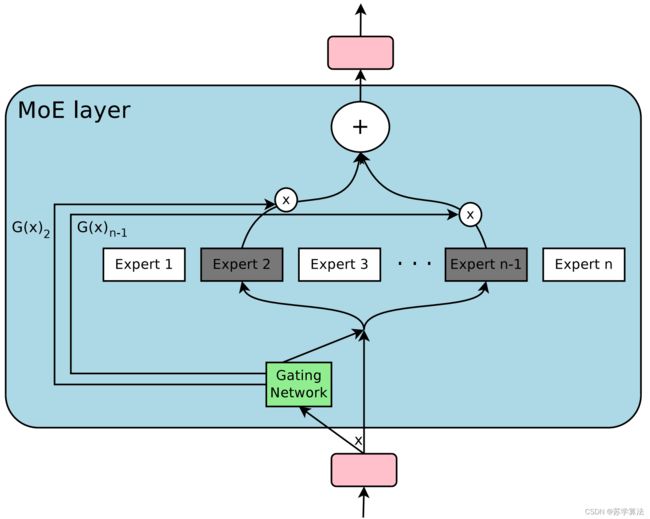
y = ∑ i = 1 n G ( x ) i E i ( x ) y=\sum_{i=1}^{n} G(x)_{i} E_{i}(x) y=i=1∑nG(x)iEi(x)
其中,输入为 x x x, E i E_{i} Ei 表示第 i i i 个专家网络, G ( x ) i G(x)_{i} G(x)i 表示第 i i i 个门控网络,输出 y y y 可以理解为是对多个专家意见的加权求和。
MoE 可以作为一个基本的组成单元,也可以是多个 MoE 结构堆叠在一个大网络中。比如一个 MoE 层可以接受上一层 MoE 层的输出作为输入,其输出作为下一层的输入使用。在谷歌大脑的论文中,MoE 就是作为循环神经网络中的一个循环单元。
MoE 神经网络结构优点如下:
-
实现一种多专家集成的效果
MoE 的思想是训练多个神经网络(也就是多个专家),每个神经网络(专家)通过门控网络(Gating NetWork)被指定应用于数据集的不同部分,最后再通过门控网络将多个专家的结果进行组合。单个模型往往善于处理一部分数据,不擅长处理另外一部分数据(在这部分数据上犯错多),而多专家系统则很好的解决了这个问题:系统中的每一个神经网络,也就是每一个专家都会有一个擅长的数据区域,在这组区域上该专家就是 “权威”,要比其他专家表现得好。因此多专家系统是单一全局模型或者多个局部模型的一个很好的折中,这样的网络结构能够处理更加复杂的数据分布,在相应的任务中,性能也会有很大的提升。 -
只需增加很小的计算力,便能高效地提升模型的性能
神经网络吸收信息的能力受其参数数量的限制。有人在理论上提出了条件计算(conditional computation)的概念,作为大幅提升模型容量而不会大幅增加计算力需求的一种方法。MoE 就是条件计算的一种实现,并在论文中证实,这种网络结构可实现在计算效率方面只有微小损失情况下,可以显着提高性能。
三、MoE与MTL的结合
3.1 模型结构
接下来我们来看 MoE 如何与 MTL 结合。
MTL 最经典的 Shared-Bottom DNN 网络结构,如下图所示
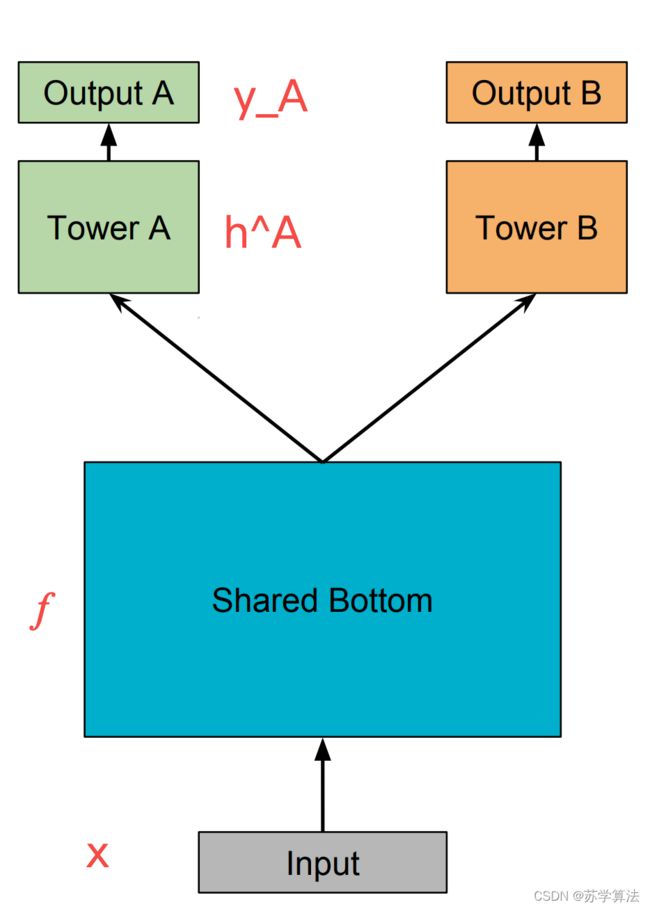
Shared-Bottom 网络通常位于底部,表示为函数 f f f,该层被多个任务共用。往上, k k k 个子任务分别对应一个 tower network,表示为 h k h^k hk,第 k k k 子任务的输出 y k = h k ( f ( x ) ) y_k = h^k(f(x)) yk=hk(f(x))。
然后用一组由专家网络(expert network)组成的神经网络结构来替换掉 Shared-Bottom 部分(函数 f f f ),这里的每个 “专家” 都是一个前馈神经网络,再加上一个门控网络,就构成了 MoE 结构的 MTL 模型。因为只有一个门网络,所以在论文中,为了与 MMoE 对应,也称这种结构为 OMoE(One-gate Mixture-of-Experts),其结构如下图所示:

MoE 模型可以表示为:
y = ∑ i = 1 n g ( x ) i f i ( x ) y=\sum_{i=1}^{n} g(x)_{i} f_{i}(x) y=i=1∑ng(x)ifi(x)
其中, f i ( i = 1 , . . . , n ) f_i (i = 1, ..., n) fi(i=1,...,n) 是 n n n 个专家(expert)网络, g g g 是组合 experts 结果的门控网络(gating network) ∑ i = 1 n g ( x ) i = 1 \sum_{i=1}^{n} g(x)_{i}=1 ∑i=1ng(x)i=1。具体而言,门控网络 g g g 产生 n n n 个 experts 上的概率分布,最终的输出是所有 experts 的加权求和。MoE 可看做基于多个独立模型的集成方法。
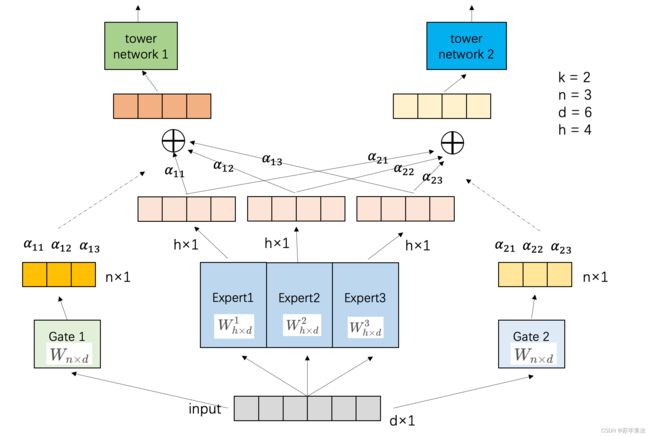
顾名思义,MMoE(Multi-gate Mixture-of-Experts)就是在 OMoE 的基础上,用了多个门控网络,结构如下图所示:

MMoE 表示为
y k = h k ( f k ( x ) ) , f k ( x ) = ∑ i = 1 n g k ( x ) i f i ( x ) y_{k}=h^{k}\left(f^{k}(x)\right), f^{k}(x)=\sum_{i=1}^{n} g^{k}(x)_{i} f_{i}(x) yk=hk(fk(x)),fk(x)=i=1∑ngk(x)ifi(x)
其中,门控网络 g k ( x ) = softmax ( W g k x ) g^{k}(x)=\operatorname{softmax}\left(W_{g k} x\right) gk(x)=softmax(Wgkx),其输入为 input feature,输出就是所有 Experts上的权重。 x x x 表示输入 input, W g k ∈ R n × d W_{g k} \in \mathbb{R}^{n \times d} Wgk∈Rn×d 表示一个可训练的矩阵, n n n 是专家的个数, d d d 是特征的维度。 h k h^k hk 表示 tower network。
可见 MMoE 其实是 MoE 针对 MTL 的变种和优化,相对于 OMoE 的结构中所有任务共享一个门控网络,MMoE 的结构优化为每个任务都单独使用一个门控网络。这样的改进可以针对不同任务得到不同的 Experts 权重,从而实现对 Experts 的选择性利用,不同任务对应的门控网络可以学习到不同的 Experts 组合模式,因此模型更容易捕捉到子任务间的相关性和差异性。
3.2 维度分析
参数含义
d:输入特征的维度
h:每个expert 输出的神经元数
n:专家expert数
k:子任务数量
专家网络的维度: W n × h × d W_{n \times h \times d} Wn×h×d
门控网络的维度: W k × n × d W_{k \times n \times d} Wk×n×d
n n n 个专家网络的输出 y ∈ R n × h y \in R^{n \times h} y∈Rn×h
y = f ( x ) = W n × h × d x y=f(x)=W_{n \times h \times d} x y=f(x)=Wn×h×dx
k k k 个门控网络的输出 z ∈ R k × n z \in \boldsymbol{R}^{k \times n} z∈Rk×n
z = g ( x ) = softmax ( W k × n × d x ) z=g(x)=\operatorname{softmax}\left(W_{k \times n \times d} x\right) z=g(x)=softmax(Wk×n×dx)
四、MMoE的性能提升
论文分别在以下三个数据集上进行了实验,来从不同的角度验证 MMOE 的性能。
4.1 人工合成数据集(Synthetic Dataset)
因为在真实数据集中我们无法准确度量和控制任务之间的相关性,不太方便研究任务相关性对多任务模型的影响,因此在论文中,人工构建了两个回归任务的数据集,并通过正弦函数来引入非线性机制。如此可以利用两个任务标签的皮尔逊相关系数作为任务相关性的度量,来观察在不同相关性的任务下,Shared-Bottom、OMoE、MMoE 三种结构在训练过程中对 loss 的影响,最终结果如下图:
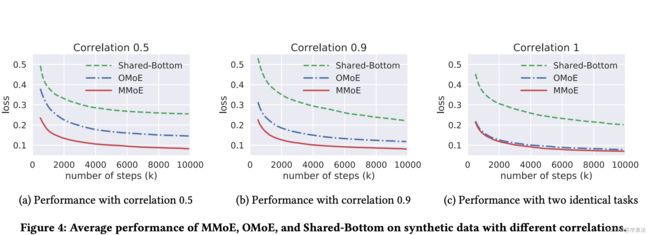
可以得出如下结论:
- OMoE 和 MMoE 的效果在不同相关度任务的数据中都好于 Shared-Bottom;
- 如果任务相关度非常高,则 OMoE 和 MMoE 的效果近似;
- 但是如果任务相关度很低,则 OMoE 的效果相对于 MMoE 明显下降,说明 MMoE 中的 multi-gate 的结构对于任务差异带来的冲突有一定的缓解作用。
此外, 在这组实验中,作者还发现 MMoE 更容易训练,并且在多次训练运行时收敛到更好的损失。这一发现也与最近的研究结果一致,门控机制在训练非凸深层神经网络时可以提高模型的可训练性。(模型的可训练性,就是指模型在超参数设置和模型初始化范围内的鲁棒性。)
论文针对数据和模型初始化中的随机性研究模型的鲁棒性,并在每种设置下重复进行多次实验,每次从相同的分布生成数据,但随机种子不同,并且模型也分别初始化,绘制了重复运行的最终损失值的直方图:
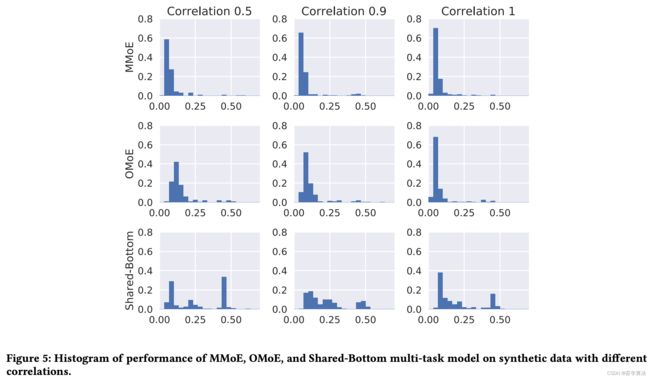
从直方图中可得出如下结论:
- 首先,在所有任务相关性设置中,Shared-Bottom 模型的性能差异(方差)远大于基于 MoE 的模型的性能差异(方差)。这意味着,与基于 MoE 的模型相比,Shared-Bottom 模型通常具有较差的局部最小值。
- 其次,虽然任务相关性为 1 时 OMoE 模型的性能方差与 MMoE 模型相似,但当任务相关性降低到 0.5 时,OMoE 的鲁棒性明显下降。MMoE 和 OMoE 之间的唯一区别是是否存在多门结构。这验证了多门结构在解决由任务差异造成的不良局部最小值方面的有用性。
- 最后,值得一提的是,这三个模型中的最低损失是可比的(差异不悬殊)。这并不奇怪,因为神经网络在理论上是通用近似器。具有足够的模型容量,应该存在一个 “正确” 的共享底部模型,该模型可以很好地学习这两个任务。但这只是 200 个独立实验的分布,对于更大,更复杂的模型(例如,当共享底层网络是递归神经网络时),获得任务关系 “正确” 模型的机会会更低,如果这样,仍然需要对任务关系进行显式建模。
4.2 UCI 人口普查收入数据集(UCI Census-income Dataset)
论文进一步评估了 MMoE 在基准数据集 UCI 人口普查收入数据集上的表现,并与几种最先进的多任务模型进行了比较,这些模型通过软参数共享对任务关系进行建模,两组结果数据如下:
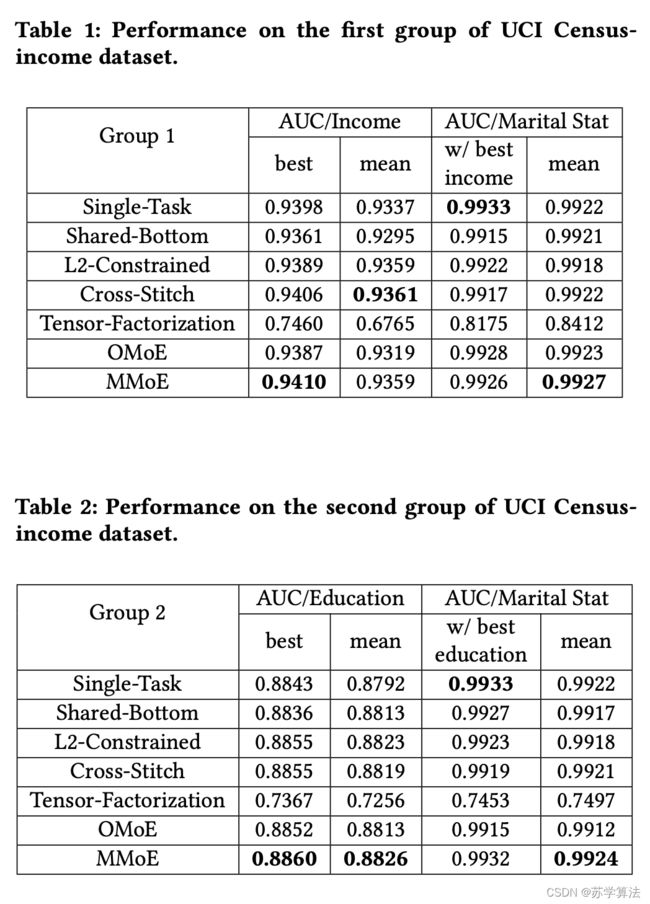
4.3 大规模内容推荐数据集
最后,论文在真实的大型内容推荐系统上测试 MMoE,在向用户推荐项目时可同时学习两个分类任务。实验使用了数千亿个训练样本来训练 MMoE 模型,并将其与基于 Shared-Bottom 的生产模型进行比较,见下图。从结果来看,AUC 等离线性能指标有着显著的提高。
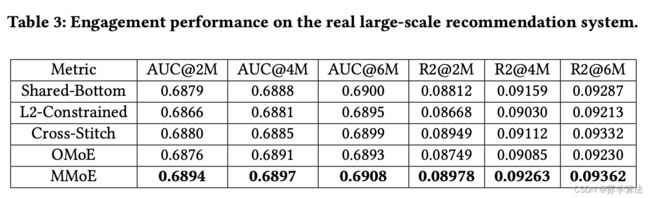
同时,实时实验中也发现 MMoE 的在线指标表现也不错。
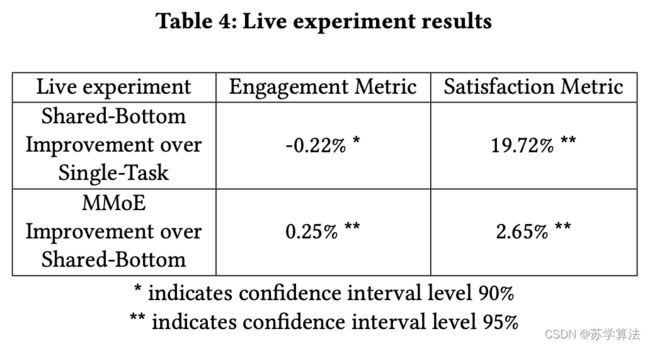
五、代码实现
参考代码:
- keras demo
- github2(浅梦学习笔记)5.9K star
核心代码
class MMoE_Layer(tf.keras.layers.Layer):
def __init__(self,expert_dim,n_expert,n_task):
super(MMoE_Layer, self).__init__()
self.n_task = n_task
self.expert_layer = [Dense(expert_dim,activation = 'relu') for i in range(n_expert)]
self.gate_layers = [Dense(n_expert,activation = 'softmax') for i in range(n_task)]
def call(self,x):
# 构建多个专家网络
E_net = [expert(x) for expert in self.expert_layer]
E_net = Concatenate(axis = 1)([e[:,tf.newaxis,:] for e in E_net]) # 维度 (bs,n_expert,n_dims)
# 构建多个门网络
gate_net = [gate(x) for gate in self.gate_layers] # 维度 n_task个(bs,n_expert)
# towers计算:对应的门网络乘上所有的专家网络
towers = []
for i in range(self.n_task):
g = tf.expand_dims(gate_net[i],axis = -1) # 维度(bs,n_expert,1)
_tower = tf.matmul(E_net, g,transpose_a=True)
towers.append(Flatten()(_tower)) # 维度(bs,expert_dim)
return towers
参考
- 推荐系统中的多任务学习(卢明冬)
- 详解谷歌之多任务学习模型MMoE(KDD 2018) (知乎)
- MMOE论文笔记
- 大厂技术实现 | 多目标优化及应用(含代码实现)
- Keras实现简单Demo