流水作业调度问题
一、实验目的
1.掌握基于动态规划的算法求解流水线最优调度问题的原理。
2.掌握最优调度问题动态规划递推方程的推导过程和设计原理。
3.掌握基于动态规划方法求解流水线最优调度问题函数的具体步骤。
4.具备运用动态规划的思想设计算法并用于求解其他实际应用问题的能力。
5.深刻体会动态规划算法求解问题的便利和动态规划算法对于计算机求解该问题的 优化以及是如何简化计算步骤和减少求解问题时间的。
二、实验环境
操作系统:Windows10
实验平台:CodeBlocks
编译器:Gcc
实验语言:C++
三、实验内容
对于N个作业{1,2,………,n},和两台机器M1和M2组成的流水线。现要使N个作业在机器M1和M2上完成加工。每个作业加工的顺序已知,都是先在M1上加工,然后在M2上加工。
在加工作业所花费的时间上,M1加工作业i所需的时间为ai,M2加工作业i所需的时间为bi,i为作业序号,1≤i≤n。流水作业调度问题要求确定这n个作业的最优加工顺序,使得从第一个作业在机器M1上开始加工,到最后一个作业在机器M2上加工完成所需的时间最少。
四、算法描述
通过分析问题可知,要使得调度顺序为最优调度,机器M1应该没有空闲时间,而且机器M2的空闲时间最少。而在一般情况下,机器M2上作业有两种情况:机器空闲或作业积压。分析可知,最优调度应该满足以下情况:
①机器M1上所有作业的加工时间为ai之和,即要求机器M1上的加工是不间断的,机器M2上所有作业的加工时间不一定为bi之和,即对机器M2上的加工间断问题不要求。
②对于机器M1和机器M2,要求作业在两台机器上的加工次序是完全相同的。
分析以上两种情况可知,对于流水线最优调度问题,仅需考虑在两台机器M1和M2上加工次序完全相同的调度。
设全部作业的集合为N={1,2,…,n}。S是N的作业子集。在一般情况下,对于机器M1,在其加工作业子集S中作业时,机器M2还在加工其他作业,在等待时间t后,机器M2可以再次加工作业。对于这种情况,将完成S中作业所需的最短时间记为T(S,t),而流水作业调度问题的最优值为T(N,0)。
流水线调度问题的最优子结构性质:记ai(选定的作业i在机器M1上的加工时间),T(N-{i},bi}(剩下的作业要等bi时间后才能在M2上加工),流水线作业调度开始时,工作i随机抽取,M1加工完并花费时间ai之后,开始加工bi,M1空闲,开始加工所剩下的N-i个作业,此时M2开始加工,需要时间bi完成,等待bi时间之后可以重新利用机器M2,最优解可表示为T(N,0)=min{ai + T(N-{i},bi)}, i∈N,需要枚举所有的工作i,使T(N,0)取得最小值。
一般情况下,有递推关系式:
TS,t=min{ai+Ts-i,bi+maxt-ai,0}
由Johnson法则可知,任意两个满足Johnson法则的调度应该具有相同的加工时间,即满足Johnson法则调度均为最优调度,可知,流水线作业调度问题可以转化为求解满足Johnson法则的调度问题。
综上可知,对于流水线调度的最优解问题,一定存在满足Johnson法则的最优调度,求解过程可由以下三个步骤确定:
①把所有作业按M1,M2的时间分为两组,a[i]<=b[i]对应第一组N1,a[i]>b[i]对应第0组N2。
②将N1中的待调度作业按照ai的递增排序,将N2中的待调度作业按bi的递减排序。
③按顺序先执行N1中的作业,再执行N2中的作业,得到的就是耗时最少的最优调度方案。
五、实验结果
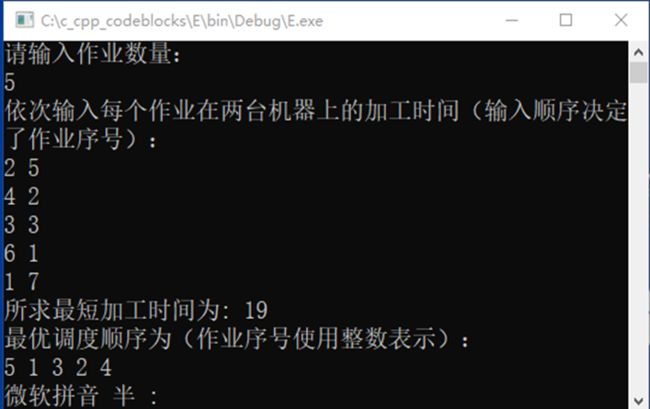
第一组输入,设输入的作业数量为5个,按照作业顺序(1,2,3…)输入,输入2,4,3,6,1为作业i在第一个机器M1上加工所需要的时间,输入5,2,3,1,7为作业i在第二个机器M2上加工所需要的时间。通过所编写程序求得加工所需的最短时间为19,最优调度顺序为5,1,3,2,4。
第二组输入,设输入的作业数量为7个,按照作业顺序(1,2,3…)输入,输入5,3,6,4,8,9,6为作业i在第一个机器M1上加工所需要的时间,输入2,4,7,2,9,7,3为作业i在第二个机器M2上加工所需要的时间。通过所编写程序求得加工所需的最短时间为43,最优调度顺序为2,3,5,6, 7, 4, 1。
六、实验总结
通过本次实验,我认识到为求解流水线最优调度问题,关键是根据Johnson不等式排序得到结果,Johnson不等式保证了,a < b的那个集合中的任务使用不等式排序一定比b>a的那个集合中的元素靠前。同时了解到算法设计过程中,使用Sturct结构或类来描述ADT抽象数据类型,可以使的算法的设计更加简洁明了。
通过设计算法求解该问题,我也深刻理解了动态规划算法的几个基本步骤。动态规划的算法设计中,建立递归关系是很关键的一步(确定状态转移方程),是整个动态规划算法的精髓。掌握了递归的思想,就可以完成很多不必要的重复计算。
#include
#include
using namespace std;
const int maxn = 100;
//maxn为最大作业数
int m1[maxn], m2[maxn], order[maxn];
//m1,m2数组说明了分别在m1,m2机器上的运行时间,order数组为作业的最终调度顺序
int m;
//m为作业数量
struct CJobType
{
int key,index;
bool job;
};
//函数cmp用于升序排序作业
bool cmp(CJobType a, CJobType b){
return a.key < b.key;
}
int FlowShop(int n,int a[],int b[],int c[]){
int j = 0;
int k = n - 1;
CJobType *d = new CJobType[n];
for(int i = 0; i < n; i++){
if(a[i] < b[i]){
d[i].job =true;
d[i].key =a[i];
}else{
d[i].job=false;
d[i].key=b[i];
}
d[i].index=i;
}
sort(d,n+d,cmp);
for(int i=0;i> m;
cout << "依次输入每个作业在两台机器上的加工时间(输入顺序决定了作业序号):" << endl;
for(int i = 0; i < m; i++)
cin >>m1[i] >> m2[i];
cout << "所求最短加工时间为: ";
cout << FlowShop(m,m1,m2,order) << endl;
cout << "最优调度顺序为(作业序号使用整数表示):" << endl;
for (int i = 0; i < m; i++)
cout<