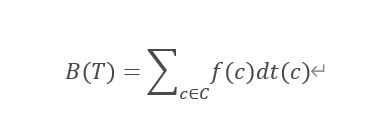实现哈夫曼编码

一、实验目的

1.掌握基于贪心的算法求解哈夫曼最优前缀编码问题的原理和贪心性质的证明。

2.掌握哈夫曼最优前缀编码贪心算法正确性的推导过程和设计原理。

3.掌握基于动态规划方法求解哈夫曼最优前缀编码问题函数的具体步骤。

4.具备运用贪心算法的思想设计算法并用于求解其他实际应用问题的能力。

5.深刻体会贪心算法求解问题的便利和贪心算法对于计算机求解该问题的优化以及是如何简化计算步骤和减少求解问题时间的。

二、实验环境

操作系统：Windows10

实验平台：VisualStudio Code

编译器：g++

实验语言：C++

实验终端：WindowsPowerShell

三、实验内容

对于数据文件的压缩，哈夫曼编码时有效的编码方式，可以对文件的压缩达到不错的压缩率。该算法根据文件中的每个字符出现的频率，生成每个字符的01字符串表示，其中，每个字符串编码都是最有前缀编码，以防止编码出现歧义。

对于一个文件，若采用定长编码的模式，通常比使用哈夫曼编码使用更多的二进制位数，变长码即哈夫曼编码通过对出现频率高的字符较短的编码，出现频率较低的字符以较长的编码，用以有效减少整体的编码的长度。

如现给出各个字符出现的频率表，对比定长编码和哈夫曼编码的区别

	A	B	C	D	E	F
频率	45	13	12	16	9	5
定长码	000	001	010	011	100	101
变长码	0	101	100	111	1101	1100

通过计算可知，定长编码的wpl为300，而哈夫曼编码的wpl为224，可见，通过哈夫曼编码，可极大的减少文本编码所需要的空间。

现在给出n个字符，并输入各个字符在一个文件中出现的频率，要求给出这些字符的最优前缀编码，即这些字符的哈夫曼编码，以达到节省存储空间的目的。

四、算法描述

通过分析问题可知，哈夫曼最优前缀编码的生成要求任意字符的代码都不是其他字符编码的前缀。同时，对于译码过程也不能太复杂，需要一个合适的数据结构来表示字符的最优前缀码，对于最优前缀码的表示，这个合适的数据结构就是完全二叉树。

在表示前缀码的二叉树中，树叶代表每个需要编码的字符，树的路径，即从树根到每个树叶的通路，若某节点位于一树枝的左侧，则编码为0，若位于一树枝的右侧，则编码为1，即编码中每一位的0和1分别表示某结点到左儿子和右儿子的路标。

通过分析得到，表示最优前缀码的二叉树总是一个完全二叉树，树中每一个节点都有2个儿子，对于定长编码来说，其编码二叉树就不是一棵完全二叉树，存在优化的可能。为方便分析问题，现给定C为编码字符集，在最优前缀编码的二叉树中，这些字符集为该二叉树的各个叶子节点，每个叶子节点对应字符集中的一个字符，该完全二叉树优C-1个内部节点。

若给定编码字符集C和每个字符对应的出现频率f，即C中的每一字符都各以频率f(c)在需要压缩和编码的文件中出现，C的每一个前缀编码方案都对应一棵二叉树T，字符C在树中的深度记为dt(c), dt(c)也是字符c的前缀码长度，通过以上分析可知，该编码方案的平均码长定义为：

可以使平均码长达到最小的前缀编码方案称为C的最优前缀码。

求解最优前缀编码的贪心算法，该算法通过自底向上的方式构造表示最优前缀编码的二叉树T，该算法从C个叶子节点开始，执行C-1次合并后产生最后所要求的完全二叉树。

贪心求解哈夫曼编码的贪心选择性质：设C为编码字符集，C中字符c频率为f（c），设x，y是C中具有最小频率的两个字符， 则存在C的最优前缀码使得x和y具有相同的编码长度并且仅有最后一位编码不同。

贪心求解哈夫曼编码的最优子结构性质：设T为表示字符集C的一个最优前缀编码的完全二叉树，设x和y为树T的两个叶子节点且为兄弟，z为它们的父亲，若将z看作具有频率f（z）= f（x）+ f（y）的字符，则树T’=T-{x,y}表示字符集C’=C-{x,y}U{z}的一个最优前缀码。

贪心求解的贪心选择性质和最优子结构性质表明了最优前缀码的存在，并且最优前缀码不一定相同，但是其表示的WPL是相同的。

为求解最优前缀编码问题，首先定义两个结构体，首先是字符结构体，该结构体包含了每个字符和该字符的编码，编码使用双端队列保存。

struct Hcode

{

char ch;

dequehuffcode;

};

同时，创建一个字符节点的结构体，对于每个节点，保存该节点的父亲，儿子，以便容易根据函数求出哈夫曼编码

struct Hnode

{

int weight = 0;

Hnode* parent = NULL;

Hnode* Lchild = NULL;

Hnode* Rchild =NULL;

};

该贪心算法的主要思想是，通过编码中每个字符所对应的频率f（c），使用优先队列（小顶堆）贪心的选择当前需要合并的两棵具有最小频率的树，当合并完两棵具有最小频率的树后，将该树插入优先队列，该树的频率为合并的两棵树的频率之和。

构建哈夫曼二叉树具体步骤如下(对应代码中buildTree函数的实现):

1. ：判断当前优先队列的大小是否为一，若为一，表示合并完毕（二叉树构建完毕），可以返回。若不为一，则进入如下步骤。

2. ：新建一个树节点，同时从优先队列中取出两个节点，由于最小堆的性质，所取出的两个节点必然是当前节点中频率最小的两个。

3. ：对新建的树节点，其权重之和,即频率之和为当前节点中频率最小的两个的频率之和。

4. ：将新建的树节点插入优先队列，直到二叉树构建完毕。

构建哈夫曼编码的具体步骤如下(对应代码中obtainCode函数的实现)：

5. ：对于每个叶子节点（使用结构体Hnode表示），循环遍历，总过需要查询n次，n为字符集C的大小。

6. ：对于当前节点的查询，若当前节点为父节点的右儿子，在该节点的字符编码队列中插入1（节点使用结构体Hcode表示）。

7. : 对于当前节点的查询，若当前节点为父节点的左儿子，在该节点的字符编码队列中插入0。

8. : 若当前节点查询完毕，则迭代至其父节点，直到确定完每个字符的编码，编码保存在每个字符的编码队列中。

五、实验结果

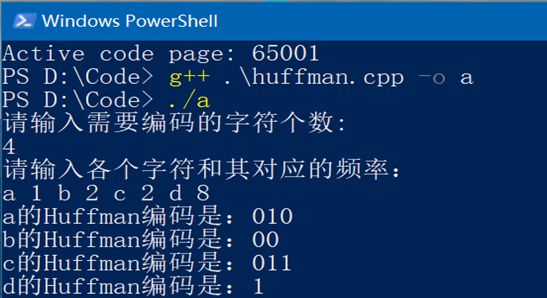
第一组输入，设需要编码的字符个数为4个，分别为a，b，c，d，每个字符对应的频率为1，2，2，8。通过所编写程序求得字符a的编码为010，字符b的编码为00，字符c的编码为011，字符d的编码为1，其WPL为21。

第二组输入，设需要编码的字符个数为4个，分别为a，b，c，d，每个字符对应的频率为3，3，3，3。即每个字符在文本中出现的频率相同，通过所编写程序求得字符a的编码为00，字符b的编码为10，字符c的编码为01，字符d的编码为11，和定长编码相同。其wpl为24。

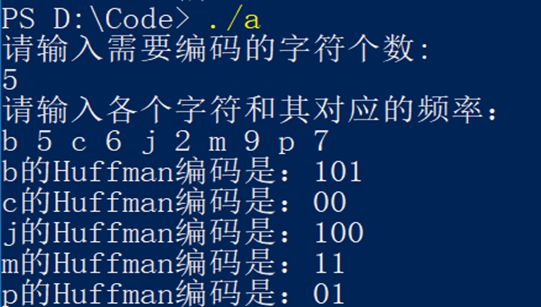
第三组输入，设需要编码的字符个数为5个，分别为b，c，j，m，p每个字符对应的频率为5，6，2，9，7。通过所编写程序求得字符b的编码为101，字符c的编码为00，字符j的编码为100，字符m的编码为11，字符p的编码为01。其wpl为45。

六、实验总结

本次实验从压缩文件的实例出发，通过对比定长编码和哈夫曼编码在编码长度上的区别，引出了哈夫曼编码问题，并且通过实例体会到了哈夫曼编码对于优化和减少存储空间的好处。

通过学习哈夫曼算法的贪心求解，我掌握了哈夫曼算法的贪心选择性质和最优子结构性质，这两个性质表明了最优前缀码的存在，并且最优前缀码不一定相同，但是其表示的WPL是相同的，如在第三组输入中，输入的例子和讲义上相同，得到的前缀码却不同，通过计算可知，这两个编码的WPL是相同的，表示该编码依然是哈夫曼编码。

贪心算法虽然不能得到整体最优解，但其最终结果依然是最优解的很好近似解，在代码实现上，课本上提供了单个结构体的算法实现，但通过上机编程，我意识到求解哈夫曼树是简单的，但是对于哈夫曼编码的获取却实在不容易，只能通过再次建立一个Hcode的结构体用于保存每个字符的哈夫曼编码。第二个难点是C++语言中优先队列的使用，优先队列保存int等基本类型，对基本类型建立最大最小堆容易，但是对于自定义的结构体，和自定义的排序规则，却只能通过仿函数实现，增加了编程的难度和不必要的麻烦。

通过这次求解实现哈夫曼编码的实验，增加了对于C++编码灵活性的认识以及对于贪心算法的深刻理解。

#include
#include
using namespace std;
const int maxn = 128;
//maxn表示最多可对128个字符进行编码

//字符结构体 包含字符和字符的双端队列保存的编码
struct Hcode
{
    char ch;
    deque huffcode;
};

//Huffman树节点
//对于每个节点，保存其的父亲，儿子，以便容易根据函数求出哈夫曼编码
struct Hnode
{
    int weight = 0;
    Hnode* parent = NULL;
    Hnode* Lchild = NULL;
    Hnode* Rchild = NULL;
};

//此为优先队列的cmp函数,按照字符节点的权重，构造出来的小顶堆
struct cmp
{
    bool operator() (const Hnode* a, const Hnode* b)
    {
        return a->weight > b->weight;
    }
};

//node数组用于存放字符节点，即叶子节点
//code数组用于存放字符结构体
Hnode node[maxn];
Hcode code[maxn];
priority_queue, cmp> pq;
int n;


//Huffman树构造函数
//将各个node的指针存入优先队列中，每次取出一个，按照哈夫曼树的构造规则进行构造，即对每个结点的父亲和儿子进行设置
void buildTree(priority_queue, cmp>& pq)
{
    //当优先队列中剩余一个元素时，表示树构建完毕
    while (pq.size() != 1){
        Hnode *Pnode = new Hnode();

        Hnode* first = pq.top();
        pq.pop();
        Hnode* second = pq.top();
        pq.pop();

        Pnode->weight = first->weight + second->weight;

        Pnode->Lchild = first;
        Pnode->Rchild = second;

        first->parent = Pnode;
        second->parent = Pnode;
        //由于每个字符的节点都是叶子节点，只需通过指针设置他们的父亲即可
        pq.push(Pnode);
    }
}

//Huffman编码获取函数
void obtainCode(Hnode* node, Hcode* code)
{
    for(int i=0; i < n; i++)
    {
        Hnode* tmp = &node[i];

        while(1){
            if (tmp->parent == NULL) break;
            else{
                 if (tmp->parent->Rchild == tmp)//我是父亲的右儿子，我应该添加编码1
                    code[i].huffcode.push_front(1);
                 else
                    code[i].huffcode.push_front(0);//我是父亲的左儿子，我应该添加编码0
            }
            tmp = tmp->parent;//轮到我父亲了
        }

    }
}

//Huffman编码输出函数
void printCode(Hcode* code)
{
    deque::iterator it;

    for(int i=0; i> n;

    cout << "请输入各个字符和其对应的频率：" << endl;
    for (int i = 0; i < n; i++)
        cin >> code[i].ch >> node[i].weight;

    //对优先队列进行初始化
    for(int i=0; i