举例说明神经网络运行机制(附用numpy从零实现神经网络)

举例说明神经网络运行机制(附用numpy从零实现神经网络)

1.数据,问题,目的

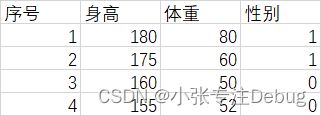
数据如上图所示,输入为身高体重,输出为性别(1:男,0:女)。
目的:搭建一个神经网络,通过四条数据训练模型参数使模型可以根据输入给出输出。

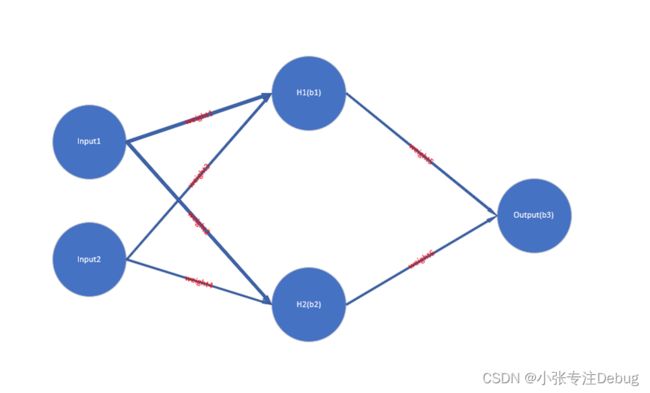
Input:输入
Output :输出
Weight:实体权重

2.前向传播

(1)将身高作为input1,体重作为input2。
(2)H1 =f [(input1 * weight1) +(input2 * weight3) + b1],f[x]:激活函数，激活函数存在的意义是：采用非线性激活函数使整个网络非线性化，具备更强的拟合能力；使方向传播变的可能。因为，这时候梯度和误差会被同时用来更新权重和偏移。没有可微分的线性函数，这就不可能了。

def sigmoid(x):
    '''
    激活函数 f(x) = 1 / (1 + e^(-x))
    '''
    return 1 / (1 + np.exp(-x))

(3)H2 =f [(input1* weight2) +(input2 * weight4) + b2]
（4）output = f[(H1 * weight5) + (H2 * weight6) + b3],此时就得到了模型的预测值，前向传播就完成了。

3.反向传播

根据上述的前向传播得到的预测值，显然是不可靠的，因为权重并不是最优的。因此评判模型被训练到了一个什么样的程度以及如何迭代更新权重（包括如何更新权重）就成了重要的问题。
(1)评判标准：loss = ∑(y(true)-y(pred))(y(true)-y(pred))/n，loss值就是对送入训练的所有样本的真实值减去预测值的平方进行求平均值。

def mse_loss(y_true, y_pred):
    '''
    计算模型对某一样本的预测值与真实值之间的差别
    '''
    return ((y_true - y_pred) ** 2).mean()

(2)显然，上述的loss值越接近于0，证明预测值越接近真实值。输入是相同的，激活函数是相同的，最终能改变预测结果的就是可变的参数，可变的参数为weight1,weight2,weight3,weight4,weight5,weight6,b1,b2,b3,那么我们就需要更改这些参数来试着减小loss。
这些参数如何更改才会使得loss变小呢？（不妨把loss看成以权重和偏置为自变量的函数）
我们可以用loss值对每个权重求偏导，如果某一个结果为正，表示增加这个权重loss值就会相应的增加。

相同的道理可以计算loss对每个权重和偏置的偏导数。
(3)之后我们根据（2）中得到的结果对权重和偏执进行更新，更新的公式如下：
weight = weight -lr * (偏导数值)
b = b -lr * (偏导数值)

                # 参数更新
                self.w1 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_w1
                self.w2 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_w2
                self.b1 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_b1

                self.w3 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_w3
                self.w4 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_w4
                self.b2 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_b2

                self.w5 -= learn_rate * d_L_d_ypred * d_ypred_d_w5
                self.w6 -= learn_rate * d_L_d_ypred * d_ypred_d_w6
                self.b3 -= learn_rate * d_L_d_ypred * d_ypred_d_b3

(4)将更新完的参数再放回网络中，再进行前向传播，计算loss,求偏导，更新参数一系列的循环，知道loss值为0为止（理论上来讲，实际上loss降到0的情况很少）。

下放完整代码：

import numpy as np

def sigmoid(x):
    '''
    激活函数 f(x) = 1 / (1 + e^(-x))
    '''
    return 1 / (1 + np.exp(-x))

def deriv_sigmoid(x):
    '''
    对sigmoid激活函数求导f'(x) = f(x) * (1 - f(x))
    '''
    fx = sigmoid(x)
    return fx * (1 - fx)

def mse_loss(y_true, y_pred):
    '''
    计算模型对某一样本的预测值与真实值之间的差别
    '''
    return ((y_true - y_pred) ** 2).mean()

class NeuralNetwork:
    def __init__(self):
        # 随机设置权重
        self.w1 = np.random.normal()
        self.w2 = np.random.normal()
        self.w3 = np.random.normal()
        self.w4 = np.random.normal()
        self.w5 = np.random.normal()
        self.w6 = np.random.normal()

        # 随机设置偏置
        self.b1 = np.random.normal()
        self.b2 = np.random.normal()
        self.b3 = np.random.normal()

    def feedforward(self, x):
        # 前向传播，计算当前节点应得到的值，对前一层所有与先节点连接的节点×权重+偏置并且激活
        # x即是train里的data里的一条数据 x[0]：该条数据的第一个特征 x[1]：该条数据的第二个特征
        h1 = sigmoid(self.w1 * x[0] + self.w2 * x[1] + self.b1)
        h2 = sigmoid(self.w3 * x[0] + self.w4 * x[1] + self.b2)
        o1 = sigmoid(self.w5 * h1 + self.w6 * h2 + self.b3)
        return o1

    def train(self, data, all_y_trues):
        '''
        输入数据为（nx2）的numpy数组，n代表有多少条数据
        输入标签为（nx1）的numpy数组，n代表有多少条数据（输入标签与输入数据一一对应）
        '''
        learn_rate = 0.1     # 学习率
        epochs = 1000        # 训练的轮次
###########################训练，迭代更新参数##############################
        for epoch in range(epochs):
            for x, y_true in zip(data, all_y_trues):
                sum_h1 = self.w1 * x[0] + self.w2 * x[1] + self.b1
                h1 = sigmoid(sum_h1)

                sum_h2 = self.w3 * x[0] + self.w4 * x[1] + self.b2
                h2 = sigmoid(sum_h2)

                sum_o1 = self.w5 * h1 + self.w6 * h2 + self.b3
                o1 = sigmoid(sum_o1)
                y_pred = o1
                # loss对参数求偏导
                d_L_d_ypred = -2 * (y_true - y_pred)

                d_ypred_d_w5 = h1 * deriv_sigmoid(sum_o1)
                d_ypred_d_w6 = h2 * deriv_sigmoid(sum_o1)
                d_ypred_d_b3 = deriv_sigmoid(sum_o1)

                d_ypred_d_h1 = self.w5 * deriv_sigmoid(sum_o1)
                d_ypred_d_h2 = self.w6 * deriv_sigmoid(sum_o1)

                d_h1_d_w1 = x[0] * deriv_sigmoid(sum_h1)
                d_h1_d_w2 = x[1] * deriv_sigmoid(sum_h1)
                d_h1_d_b1 = deriv_sigmoid(sum_h1)

                d_h2_d_w3 = x[0] * deriv_sigmoid(sum_h2)
                d_h2_d_w4 = x[1] * deriv_sigmoid(sum_h2)
                d_h2_d_b2 = deriv_sigmoid(sum_h2)

                # 参数更新
                self.w1 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_w1
                self.w2 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_w2
                self.b1 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_b1

                self.w3 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_w3
                self.w4 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_w4
                self.b2 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_b2

                self.w5 -= learn_rate * d_L_d_ypred * d_ypred_d_w5
                self.w6 -= learn_rate * d_L_d_ypred * d_ypred_d_w6
                self.b3 -= learn_rate * d_L_d_ypred * d_ypred_d_b3
#########################################################################################

            # --- Calculate total loss at the end of each epoch
            if epoch % 10 == 0:
                y_preds = np.apply_along_axis(self.feedforward, 1, data)
                loss = mse_loss(all_y_trues, y_preds)
                print("Epoch %d loss: %.3f" % (epoch, loss))
###########创建数据##############
data = np.array([
    [180, 80], 
    [175, 60],  
    [160, 50],   
    [155, 52], 
    ])
all_y_trues = np.array([
    1, 
    1, 
    0, 
    0, 
    ])
model = NeuralNetwork()
model.train(data, all_y_trues)