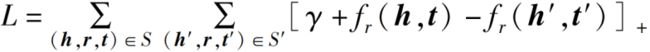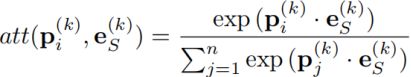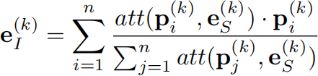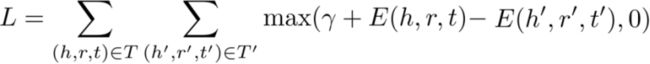知识图谱-知识表示-单模态知识表示模型TransE模型及多模态知识表示模型IKRL
本博客摘自本人研究生一年级期间参与学习中国科学院大学“地理大数据分析”课程时按照老师要求完成的“多模态知识表示”课题报告。如有异议,欢迎交流。
摘要:知识表示的目标是将人所了解的知识表示成为计算机也能理解的方式,以帮助处理下游任务。TransE模型的出现掀起了将实体和关系以三元组形式嵌入到低维空间的热潮,但TransE模型仅表示了三元组形式的知识。多模态知识表示将其他形式的知识与三元组形式的知识相结合,以产生更加精确的知识表示。本文将介绍单模态知识表示模型TransE,并基于TransE模型介绍多模态知识表示模型IKRL,使用多模态数据集WN9-IMG实现IKRL,并对IKRL算法进行了评估,认为IKRL模型的效果高于一般的单模态知识表示模型。
关键词:知识图谱,知识表示,TransE,IKRL
1 简介
1.1 知识图谱
知识图谱的起源来自于20世纪50年代末60年代初的语义网(Semantic Network),语义网是指一种基于图的存储知识的结构,图的节点代表实体,边代表实体之间的关系。20世纪80年代,知识工程的概念被提出,20世纪90年代,机构知识库的概念被提出,知识表示和知识组织问题开始被学者们深入研究(朱木易洁,2017)。2012年,谷歌提出了知识图谱(Knowledge Graph, KG)的概念,旨在以结构化的形式描述客观世界中概念、实体及其关系,将互联网的信息表达成更接近人类认知世界的形式,提供了一种更好地组织、管理和理解互联网海量信息的能力(《知识图谱发展报告》,2018)。作为了结合了数据库、自然语言处理、机器学习等多门学科的综合性学科,知识图谱不是一种新的知识工程中的某个领域,而是一种基于大数据的现代知识工程,可以说知识图谱就是这个时代所流行的知识工程。当今时代,知识图谱的应用领域十分广泛,包括数据分析、智慧搜索、智能推荐、自然人机交互、决策支持等。
1.2 知识表示
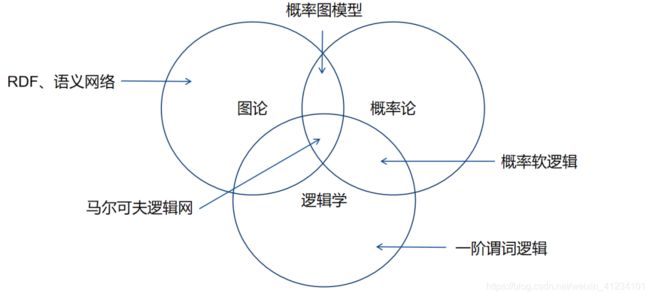
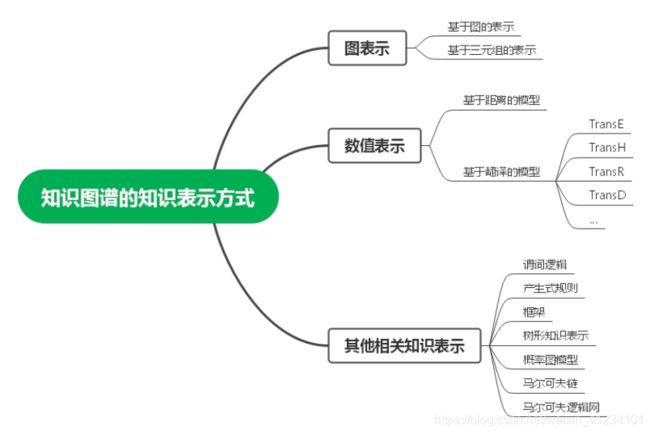
知识图谱包括了知识获取、知识表示、知识推理、知识存储、知识融合、知识建模、知识运算、知识运维等多种技术,这些技术贯穿了整个知识的生命周期,使知识图谱能够对知识进行全方位的挖掘和利用。知识表示是知识图谱领域中的一个重要的技术。知识必须经过合理的表示才能被计算机处理,知识表示学习是对现实世界的一种抽象表达。知识表示学习实现的目标是将人所了解的知识表示成为计算机也能理解的方式,以帮助处理下游任务如知识推理、知识融合、知识运算等。为了解决知识表示问题,许多学者基于图论、概率论和逻辑学对知识表示进行了研究,方式包括了资源描述框架(Resource Description Framework, RDF)、语义网络、概率图模型、概率软逻辑等,如图1。目前,知识图谱的知识表示方法主要分为图表示、数值表示和其他表示方法,如图2。
图1 知识表示研究方法归类
图2 知识图谱的知识表示方式
1.3 TransE模型
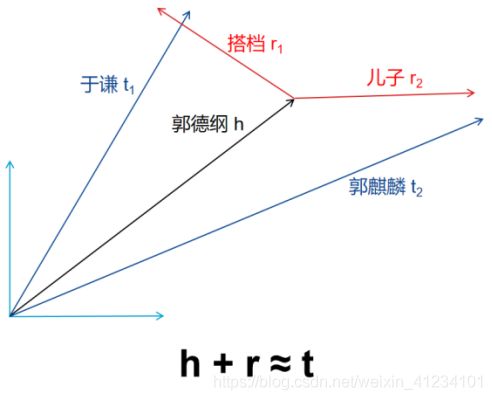
2013年,Bordes等(Bordes et al., 2013)提出了TransE模型,TransE模型将实体知识及其关系表示成一种计算机能够识别的方式:向量空间,实体及之间的关系都可看作为空间中可平移的向量,通过头实体h(head)、尾实体t(tail)和他们之间的关系r(relation)在低维向量空间中的简单向量运算h+r ≈ t,实现头实体和关系对尾实体的“翻译”(如图3),因此TransE也被称为翻译模型。
图3 TransE模型的h+r ≈ t示意图
在TransE模型中,对嵌入到低维向量空间的实体及关系的误差函数定义为:
计算的是头实体向量h通过关系向量r表达尾实体向量t时,在向量空间中的欧式距离,本质上就是计算在向量空间中实体向量及关系向量对知识进行表示时的误差程度。TransE模型的Hinge Loss函数L定义为:
其中,![]() 表示的是正确三元组集合的欧式距离,
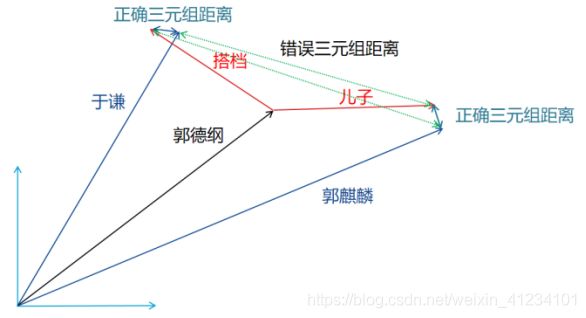
表示的是正确三元组集合的欧式距离,![]() 表示的是错误三元组集合的欧式距离,一般取任意正确三元组集合的补集作为错误的三元组集合,[ ]+表示的是正值函数,也成为ReLU激活函数,即当[ ]≥0时[ ]=[ ],当[ ]<0时[ ]=0。Hinge Loss函数定义了一种对误差的评判方式:在判断一对正确与错误的三元组时,当正确三元组距离足够短且错误三元组距离足够长,两个距离之差大于间隔参数时,则认为正确的三元组表示足够正确且错误的三元组表示足够错误,该组三元组不需要再贡献误差,若两距离之差小于间隔参数,则认为正确的三元组表示不够正确且错误的三元组表示不够错误,该组三元组的误差应计入误差函数中。Hinge的意思是“岭”,
表示的是错误三元组集合的欧式距离,一般取任意正确三元组集合的补集作为错误的三元组集合,[ ]+表示的是正值函数,也成为ReLU激活函数,即当[ ]≥0时[ ]=[ ],当[ ]<0时[ ]=0。Hinge Loss函数定义了一种对误差的评判方式:在判断一对正确与错误的三元组时,当正确三元组距离足够短且错误三元组距离足够长,两个距离之差大于间隔参数时,则认为正确的三元组表示足够正确且错误的三元组表示足够错误,该组三元组不需要再贡献误差,若两距离之差小于间隔参数,则认为正确的三元组表示不够正确且错误的三元组表示不够错误,该组三元组的误差应计入误差函数中。Hinge的意思是“岭”,![]() 就像是一个山岭,只有当正例、负例之差大到足以翻过这个“山岭”,才能够认为这组正例、负例“成功”了。这个词很生动地体现出了间隔参数
就像是一个山岭,只有当正例、负例之差大到足以翻过这个“山岭”,才能够认为这组正例、负例“成功”了。这个词很生动地体现出了间隔参数![]() 的意义。此外,这种函数还有一个很生动的名字叫做“打分函数”,就像是给一对正例负例的正确度打分一样,若“及格”则为0分,若“不及格”则打分,
的意义。此外,这种函数还有一个很生动的名字叫做“打分函数”,就像是给一对正例负例的正确度打分一样,若“及格”则为0分,若“不及格”则打分,![]() 则为“及格”的门槛。
则为“及格”的门槛。
图4 Hinge Loss函数中正确三元组距离及错误三元组距离示意图
TransE模型求解实体及其关系嵌入到低维向量空间中的目标就是寻找到实体及其关系在低维向量空间中能够满足h+r ≈ t的最优解。首先将每个实体及其关系嵌入到向量空间中的向量设为待定参数,然后利用Hinge Loss函数,通过优化求出待定系数,使得Hinge Loss函数值L最小。当正确三元组的距离越小,错误三元组的距离越大时,L就会越接近0,也就越接近实体及其关系在低维向量空间中的表示。TransE模型的算法具体步骤如图5所示。
图5 TransE模型具体步骤(Bordes et al., 2013)
与以往模型相比,TransE模型所需参数较少,计算复杂度低,但却能直接建立实体及其关系之间的语义联系,尤其在大规模稀疏知识图谱上,TransE模型的知识表示效果十分惊人(刘知远,2016)。TransE模型将实体知识与向量空间创新性地结合起来,其思想很深刻,在知识表示领域具有划时代的意义,但是由于过于简单,存在着h+r≈t假设性太强,导致在自反、一对多、多对一等关系下实体向量学习的错误,比如存在多个实体在嵌入空间中竞争一个点的情况。并且,TransE完全没有考虑语义信息,所有的实体及其关系在低维向量空间的嵌入与其本身的语义毫无关系。因此,随着TransE模型的出现,知识表示领域掀起了将实体和关系以三元组形式嵌入到低维空间以实现知识表示的热潮,包括TransD模型、TransH模型、TransR/CTransR模型、TranSparse模型等,在TransE模型的基础上对TransE模型进行了改进。
2 多模态知识表示模型IKRL
虽然TransE模型是当前知识表示领域的一大研究热点,但是2016年以前,学者们更加执着于仅仅对三元组形式的知识进行挖掘并嵌入到向量空间中。诸如TransD模型、TransH模型、TransR/CTransR模型、TranSparse模型等都基于TransE模型的基础上提高了精度,实现了对实体知识及其关系的更深层次挖掘。但是由于三元组形式的知识所包含的知识量十分有限,仅针对三元组形式的知识表示始终不能够实现计算机对知识的全方位学习。
清华大学刘知远老师课题组提出了IKRL(Image-embodied Knowledge Representation Learning)模型(Xie et al., 2016)。他们认为与其深度挖掘三元组中的知识,不如从其他模态的数据中获得补充的知识,从而优化三元组知识。IKRL使用了实体知识的视觉图像作为知识,通过增加不同模态的知识对实体知识进行了进一步的补充,从而使计算机学习到的嵌入到低维向量空间的知识更加地精确。IKRL的大致步骤如下:
- 图像编码器,将实体所对应的图像通过神经表示模块将图片中的知识嵌入到高维图像空间中,再通过图像投影模块将高维图像空间中的图像特征向量投影到低维实体向量空间中;
- 基于注意力的方法构造共同考虑每个实体所有图像实例的基于图像的表示;
- 对聚合表示的结果进行优化,即学习知识表示。
IKRL模型是第一个多模态知识表示模型。作为知识表示领域未来的发展趋势,多模态知识表示必然成为今后的研究热点。
2.1 概念定义
IKRL模型建立在TransE模型之上,因此IKRL模型中对误差函数的定义与TransE相同:
但由于IKRL模型不仅会涉及到三元组的向量,也会涉及到实体图像的向量。定义基于结构的表示(Structure-Based Representation, SBR)为在低维向量空间中的三元组向量,头实体、尾实体分别为hs、ts;定义基于图像的表示(Image-Based Representation, IBR)为在高维向量空间中的图像向量,头实体、尾实体分别为hi,ti。定义IKRL模型的总误差函数为:
![]() (4)
(4)
![]()
![]()
![]()
![]()
其中,![]() 是和TransE相同的头实体和尾实体都为SBR的误差函数,
是和TransE相同的头实体和尾实体都为SBR的误差函数,![]() 是头实体和尾实体都为IBR的误差函数,
是头实体和尾实体都为IBR的误差函数,![]() 和
和![]() 则分别选择SBR和IBR的误差函数,以确保SBR和IBR都能嵌入到同一个向量空间中。
则分别选择SBR和IBR的误差函数,以确保SBR和IBR都能嵌入到同一个向量空间中。
2.2 图像编码器(Image Encoder)
图像编码器的作用是将图像所表示的知识嵌入到TransE的向量空间中。图像编码器主要分为神经表示模块和图像投影模块。神经表示模块的作用是将图像通过神经网络提取图像特征,处理得到图像嵌入到高维向量空间的特征向量,而图像投影模块的作用是将处于高维向量空间的图像特征向量投影到TransE模型中的低维向量空间,使图像的特征向量和实体的特征向量处于同一维度上。
对于某个实体ek,存在n张各种样式的图像样例![]() 。图像表示模块使用了AlexNet作为神经网络来提取图像的特征,包含5个卷积层、2个全连接层和1个softmax层。在进行图像特征提取前,将每张图像裁剪为224×224大小,并且在第二层全连接层(也称为fc7)的输出设置为4096维。第i张图像imgi经过AlexNet处理后得到一个4096维图像空间的特征矢量
。图像表示模块使用了AlexNet作为神经网络来提取图像的特征,包含5个卷积层、2个全连接层和1个softmax层。在进行图像特征提取前,将每张图像裁剪为224×224大小,并且在第二层全连接层(也称为fc7)的输出设置为4096维。第i张图像imgi经过AlexNet处理后得到一个4096维图像空间的特征矢量![]() 。
。
图像投影模块将图像空间中的图像特征矢量投影到实体空间中,投影方式如下:
![]() (5)
(5)
其中,Pi指的是图像特征在实体空间中的矢量,M是一个di×ds投影矩阵,其中di是高维图像空间的维度,ds是低维实体空间的维度。在IKRL中,di为4096维,而ds为50维。
2.3 基于注意力的多样例学习(Attention-based Multi-instance Leaning)
一个实体的某一张对应图像经过了图像编码器处理得到了在实体空间中的特征向量表示。但是由于同一个实体常常有多张对应的图像,在实体空间中某一个实体会有对应很多个向量表示,且图像的质量往往参差不齐,因此需要使用一种表示对这些同时包含了细节信息和噪声的图像特征矢量进行整合。
IKRL使用了基于注意力的多样例学习对这些图像特征矢量进行整合处理。注意力机制源于对人类视觉的研究,由于对信息处理的瓶颈,人类只会选择性地关注所有信息中的某些部分,基于注意力的方法便是从多个样本中筛选出更加富含信息的样本。基于注意力的方法在图像分类、机器翻译、抽象化语句概括等领域应用十分广泛。
对于第k个实体的第i个图像的特征表示![]() ,该特征表示的注意力权重表示为:
,该特征表示的注意力权重表示为:
其中,![]() 表示第k个实体的SBR。同处于实体空间的SBR与各个图像的特征矢量相乘时,由于两向量间存在一定夹角,因此两向量相乘的结果便是两向量长度相乘再乘上夹角的余弦(实际情况下SBR与图像特征矢量都会归一化,因此两向量相乘便直接等于夹角的余弦)。若
表示第k个实体的SBR。同处于实体空间的SBR与各个图像的特征矢量相乘时,由于两向量间存在一定夹角,因此两向量相乘的结果便是两向量长度相乘再乘上夹角的余弦(实际情况下SBR与图像特征矢量都会归一化,因此两向量相乘便直接等于夹角的余弦)。若![]() 和
和![]() 间夹角较小,则两者相乘得到的结果会越大,此时认为该
间夹角较小,则两者相乘得到的结果会越大,此时认为该![]() 和
和![]() 结构相似,富含更丰富的信息,应当给予更多的注意力;若
结构相似,富含更丰富的信息,应当给予更多的注意力;若![]() 和
和![]() 间夹角较大,则两者相乘得到的结果会很小甚至为负数,此时认为
间夹角较大,则两者相乘得到的结果会很小甚至为负数,此时认为![]() 应是噪声,应当尽可能去除噪声对学习的影响。基于注意力从另一个角度来说就是一种权重,为了将
应是噪声,应当尽可能去除噪声对学习的影响。基于注意力从另一个角度来说就是一种权重,为了将![]() 和
和![]() 相乘的结果表示为一种权重,可以将相乘的结果放到指数上方,
相乘的结果表示为一种权重,可以将相乘的结果放到指数上方,![]() 便可使得权重大于0,同时突出注意力的权重和缩小噪声的权重。
便可使得权重大于0,同时突出注意力的权重和缩小噪声的权重。
通过上述基于注意力的方法,便可求出第k个实体的集成IBR ![]() :
:
由公式可知,![]() 本质上就是对第k个实体的多张图像的
本质上就是对第k个实体的多张图像的![]() 求加权平均,权重依据的便是上一步所求的
求加权平均,权重依据的便是上一步所求的 ![]() 。
。
2.4 目标正则化(Objective Formalization)
IKRL基于边际的打分函数定义如下:
![]()
IKRL基于边际的分数函数与TransE模型的Hinge Loss函数有许多相似之处。与TransE模型的Hinge Loss相同,![]() 是间隔参数(文献中称为余量超参数),IKRL基于边际的分数函数也使用了正例与负例,通过正例与负例之间的“距离”之差判定SBR和IBR是否足够正确,若足够正确则不贡献误差,若不够正确则将误差计算入误差函数中。唯一的区别便是IKRL基于边际的打分函数所使用的误差函数不再是TransE中简单的欧式距离了,而是式(4)和(5)中的误差函数,该误差函数包含了SBR和IBR的头实体和尾实体。
是间隔参数(文献中称为余量超参数),IKRL基于边际的分数函数也使用了正例与负例,通过正例与负例之间的“距离”之差判定SBR和IBR是否足够正确,若足够正确则不贡献误差,若不够正确则将误差计算入误差函数中。唯一的区别便是IKRL基于边际的打分函数所使用的误差函数不再是TransE中简单的欧式距离了,而是式(4)和(5)中的误差函数,该误差函数包含了SBR和IBR的头实体和尾实体。
2.5 优化过程和其它细节
与TransE相同,IKRL也是一个不断优化知识表示的过程。在整个多模态知识表示的优化过程中,有4个要优化的参数:实体在实体空间中的嵌入集合E、关系在实体空间中的嵌入集合R、在图像表示模块中神经网络的权重W和在图像投影模块的投影矩阵M。这4组参数共同组成参数集θ = {E, R, W, M}。
IKRL采用小批量随机梯度下降法(mini-batch stochastic gradient descent, SGD)优化模型,使用链规则来更新参数。在初始化过程中,M被随机初始化,E和R被随机初始化或者使用TransE模型进行预训练。在图像表示模块,IKRL使用了在ILSVRC 2012上预训练的深度学习框架Caffe进行图像表示。AlexNet的权重W通过预训练确定,在训练过程中W不会改变。
3 IKRL的实现
3.1 数据集
按照文献(Xie et al., 2016)所提供的数据,本次报告将使用WN9-IMG数据集作为进行多模态知识表示的数据集。WN9-IMG的三元组实体知识部分是提取于WordNet的知识图谱经典数据集WN18的子集,而实体对应的图像部分则来源于ImageNet,一个基于WordNet建立的巨大图像数据库,WN9-IMG提取了其中63225幅图像,并确保每个实体都有对应的多幅图像。此外,将WN9-IMG的三元组随机分为训练集、验证集和测试集。
3.2 参数设置
![]() 的参数设置经过测试,取
的参数设置经过测试,取![]() =4.0。每个实体的图像数量n=10,学习率λ的范围为[0.0002, 0.001],图像特征矢量的维度di=4096,实体空间的维度ds=50。此外,选择了TransE和TransR作为评判标准,同样地,TransE和TransR的嵌入空间维度ds=50。
=4.0。每个实体的图像数量n=10,学习率λ的范围为[0.0002, 0.001],图像特征矢量的维度di=4096,实体空间的维度ds=50。此外,选择了TransE和TransR作为评判标准,同样地,TransE和TransR的嵌入空间维度ds=50。
3.3 评估方案
由于嵌入在较高维向量空间的知识表示无法直观地让人所理解,因此需要适当的数值化的评估模型。通过本报告的结果评估模型从式(3)误差函数出发,分别对SBR和IBR两种表示求其误差函数IKRL(SBR)和IKRL(IBR),并对两个误差函数使用简单的加权平均得到IKRL(UNION),这三个误差函数将作为IKRL预测结果的误差模型。
按照TransE对模型的评估指标(Bordes et al., 2013),将使用两种类型的评估指标:正确实体的平均水平(Mean Rank)和前十个正确实体的比例(Hits@10)。
同样按照TransE对评估的设置,由于存在一些负例被错认为正例所导致的标准缺陷,将评估设置为Raw和Filter两类,其中Raw指的是直接进行评估的结果,Filter指的是在训练、验证和测试集中出现的三元组从生成的负例三元组列表中删除后再进行评估的结果。
3.4 实现代码
由于IKRL模型不仅涉及到神经网络,而且需要强大的算力,由于个人能力的有限,本人并没有成功实现IKRL模型。本报告直接使用了文献(Xie et al., 2016)中提供的在GitHub上的源代码(https://github.com/thunlp/IKRL),基于c++语言实现了IKRL模型。
3.5 实验结果
结合IKRL的实验与评估结果和文献(Bordes et al., 2013; Lin et al., 2015)的数据,汇集成表格如下:
表1 IKRL评估结果
| 模型\参数 |
Mean Rank |
Hits@10 |
||
| Raw |
Filter |
Raw |
Filter |
|
| TransE |
143 |
137 |
79.9 |
91.2 |
| TransR |
147 |
140 |
80.1 |
91.7 |
| IKRL(SBR) |
41 |
34 |
81.1 |
92.9 |
| IKRL(IBR) |
29 |
22 |
80.2 |
93.3 |
| IKRL(UNION) |
28 |
21 |
80.9 |
93.8 |
由表可见,多模态知识表示模型IKRL相比于传统的单模态表示模型TransE和TransR,在Mean Rank上很显著地更低,这是因为Mean Rank的值取决于知识表示的整体质量,对错误预测的结果很敏感。TransE模型仅仅挖掘了三元组本身的知识,很容易由于信息的缺失导致错误的关系预测,而IKRL则可以通过补充图像中的信息,减少错误预测的几率,因此IKRL的Mean Rank结果更靠前。此外,IKRL在Hits@10上也优于TransE和TransR,尤其是IKRL(UNION)的精度相比于IKRL(SBR)更高,这说明IKRL成功地将图像中的知识补充到了实体本身使得实体嵌入到向量空间中向量更加精确。
- 结论
知识图谱作为当今时代的知识工程,其所涉及的各个领域将会是未来科研工作者们的主要研究方向。在知识图谱的众多技术中,知识表示技术将人们所理解的知识结构翻译为计算机所能学习的知识,目前主流的知识表示方法便是以TransE模型为主流的低维向量空间嵌入知识表示方法。本报告对多模态知识表示领域进行了深入的学习,并且仔细地研究了第一个多模态知识表示算法IKRL。IKRL使用了三元组实体知识和实体所对应的多辐图像两种模态作为数据集,将图像所携带的知识与实体的知识融合以丰富实体知识,使得实体知识在嵌入的向量空间中能够更精确地表示实体及其关系。实验表明,IKRL能够成功地将图像知识补充到实体知识中实现更加精确的知识表示,并且相比单模态知识表示模型TransE和TransR精度更高。
本次报告没有对多模态知识表示有什么创新的想法,但本人认为多模态知识表示是一个未来知识表示技术发展的主要方向,不仅仅包括图像模态,还包括视频、语音、文本等多种模态的知识可以被补充。IKRL将图像进行特征表示,并使用投影将处于高维空间的向量放入低维空间中的思想可以进行一定的拓展,其他模态的知识也可以通过一定的处理(如神经网络)得到特征向量表示,并将该特征向量表示嵌入到实体空间中。
参考文献
Bordes A, Usunier N, Garcia-Duran A, et al. Translating embeddings for modeling multi-relational data[C]//Neural Information Processing Systems (NIPS). 2013: 1-9.
Lin Y, Liu Z, Sun M, et al. Learning entity and relation embeddings for knowledge graph completion[C]//Proceedings of the AAAI Conference on Artificial Intelligence. 2015, 29(1).
Xie R, Liu Z, Luan H, et al. Image-embodied knowledge representation learning[J]. arXiv preprint arXiv:1609.07028, 2016.
刘知远,孙茂松,林衍凯,谢若冰.知识表示学习研究进展[J].计算机研究与发展,2016,53(02):247-261.
朱木易洁,鲍秉坤,徐常胜.知识图谱发展与构建的研究进展[J].南京信息工程大学学报(自然科学版),2017,9(06):575-582.