吴恩达深度学习课程自学笔记整理(一)——一些自己总结记录的结论和小tips等

注：本人已经学完了吴恩达老师机器学习和深度学习的全部课程，整理出来的知识点是比较笼统的、自己总结的一些结论和经验，发在这里主要是为了方便自己复习翻阅，已经学完大部分课程或者对深度学习有了一定基础的uu可以阅读下~欢迎批评指正。

一些基础

逻辑回归的代价函数：

$$L(\hat{y},y)=-y\log (\hat{y})-(1-y)\log (1-\hat{y})$$ $$J(w,b)=\frac{1}{m}\sum _{i=1}^{m}L\left({\hat{y}}^{(i)},y^{(i)}\right)=\frac{1}{m}\sum _{i=1}^m\left(-y^{(i)}\log {\hat{y}}^{(i)}-\left(1-y^{(i)}\right)\log \left(1-{\hat{y}}^{(i)}\right)\right)$$

m个样本梯度下降的代码流程：

J=0;dw1=0;dw2=0;db=0;
for i = 1 to m
 z(i) = wx(i)+b;
 a(i) = sigmoid(z(i));
 J += -[y(i)log(a(i))+(1-y(i)）log(1-a(i));
 dz(i) = a(i)-y(i);
 dw1 += x1(i)dz(i);
 dw2 += x2(i)dz(i);   # 导数
 db += dz(i);
J/= m;
dw1/= m;
dw2/= m;             # 取平均
db/= m;
w=w-alpha*dw
b=b-alpha*db

向量化：

z=0
for i in range(n_x)
  z+=w[i]*x[i]
z+=b

w${}^T$X 向量化：z=np.dot(w,x)+b

import numpy as np # 导入 numpy 库
a = np.array([1,2,3,4]) # 创建一个数据 a
print(a)
# [1 2 3 4]
import time #导入时间库
a = np.random.rand(1000000)
b = np.random.rand(1000000) 
#通过 round 随机得到两个一百万维度的数组
tic = time.time() #现在测量一下当前时间
#向量化的版本
c = np.dot(a,b)
toc = time.time()
print(“Vectorized version:” + str(1000*(toc-tic)) +”ms”) 
#打印一下向量化的版本的时间
#继续增加非向量化的版本
c = 0
tic = time.time()
for i in range(1000000):
 c += a[i]*b[i]
toc = time.time()
print(c)
print(“For loop:” + str(1000*(toc-tic)) + “ms”)
#打印 for 循环的版本的时间

当我们在写神经网络程序时，或者在写逻辑(logistic)回归，或者其他神经网络模型时，应该避免写循环(loop)语句。虽然有时写循环(loop)是不可避免的，但是我们可以使用比如numpy 的内置函数或者其他办法去计算。

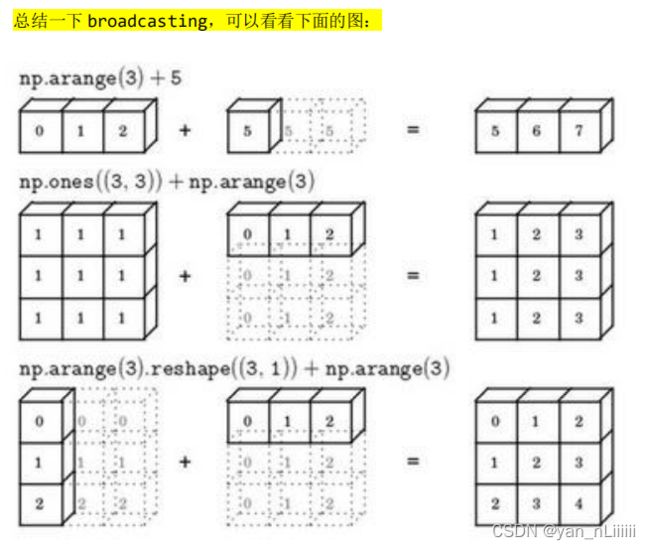
广播Broadcasting：

• 矩阵 , 和矩阵 1, 进行四则运算，后缘维度轴长度相符，可以广播，广播沿着轴长度为 1 的轴进行，即 1, 广播成为 ,′ ，之后做逐元素四则运算。
• 矩阵 , 和矩阵 ,1 进行四则运算，后缘维度轴长度不相符，但其中一方轴长度为1，可以广播，广播沿着轴长度为 1 的轴行，即 ,1 广播成为 ,′ ，之后做逐元素四则运算。
• 矩阵 ,1 和常数 进行四则运算，后缘维度轴长度不相符，但其中一方轴长度为 1，可以广播，广播沿着缺失维度和轴长度为 1 的轴进行，缺失维度就是 axis=0,轴长度为 1 的轴是 axis=1，即广播成为 ,1′ ，之后做逐元素四则运算。
  
• 一些涉及到的python编程：

import numpy as np
A=np.array ([[56.0,0.0,4.4,68.0],
           [1.2,104.0,52.0,8.0]，
           [1.8,135.0,99.0,0.9]])
cal=A.sum(axis=0)
percentage=100*A/cal.reshape(1,4)
print(percentage)

1. 来解释一下 A.sum(axis = 0)中的参数 axis，axis 用来指明将要进行的运算是沿着哪个轴执行，在 numpy 中，0 轴是垂直的，也就是列，而 1 轴是水平的，也就是行。
2. 而第二个 A/cal.reshape(1,4)指令则调用了numpy 中的广播机制。这里使用 3 × 4的矩阵除以 1 × 4的矩阵。技术上来讲，其实并不需要再将矩阵 reshape(重塑)成 1 × 4，因为矩阵本身已经是 1 × 4了。但是当我们写代码时不确定矩阵维度的时候，通常会对矩阵进行重塑来确保得到我们想要的列向量或行向量。重塑操作 reshape 是一个常量时间的操作，时间复杂度是(1)，它的调用代价极低。
3. 对于 Matlab/Octave 有类似功能的函数bsxfun

一条关于numpy使用的小tips：

举个例子，设置 = . . (5)，这样会生成存储在数组 中的 5 个高斯随机数变量。之后输出 ，从屏幕上可以得知，此时 的 shape（形状）是一个(5, )的结构。这在 Python 中被称作一个一维数组。它既不是一个行向量也不是一个列向量。
当你编写神经网络时，不要在它的 shape 是(, )即一维数组时使用数据构。应当设置 为(5,1)。如下图所示：

• 请注意一个细微的差别，在这种(5,1)结构中，当我们输出 的转置时有两对方括号，而之前只有一对方括号，所以这就是 1 行 5 列(5,1)矩阵-向量和一维数组(5,)-非向量的差别。如果你输出 (5,1)和 (5,1) 转置的乘积，会返回给你一个向量的外积，这两个向量的外积返回给你的是一个5×5矩阵。
• 老师建议，当你在编程练习或者在执行逻辑回归和神经网络时，你不需要使用这些一维数组-(5,)。如果不完全确定一个向量的维(dimension)，老师经常会扔进一个断言语句(assertion statement)：assert(a.shape==(5,1))，像这样，去确保在这种情况下是一个(5,1)向量，即一个列向量。这些断言语句是要去执行的，并且它们也会有助于为你的代码提供信息。所以不论你要做什么，不要犹豫直接插入断言语句。如果你不小心以一维数组来执行，你也能够重新改变数组维数 = ℎ(×,×)

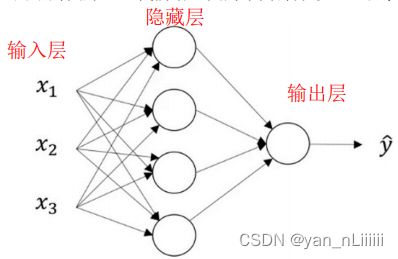
神经网络-一些符号标注

• 输入层+一个或多个隐藏层+输出层
• 当我们计算网络的层数时，输入层是不算入总层数内，所以隐藏层是第一层，输出层是第二层，有时我们将输入层称为第零层。
• 上角标1-第几层
  上角标2-第几个样本
  下角标-第几个单元/结点
  如：${}^{[2](i)}$表示第2层第i个样本

• 其中，权重矩阵W${}^{[l]}$的维度：[n${}^{[l]}$,n-1${}^{[l-1]}$]

神经网络-激活函数σ：

• sigmoid：$a=\sigma (z)=\frac{1}{1+e^{-z}}$
• tanh：$a=\tanh (z)=\frac{e^z-e^{-z}}{e^z+e^{-z}}$ ，tanh 函数是 sigmoid 的向下平移和伸缩后的结果。对它进行了变形后，穿过了(0,0)点，并且值域介于+1 和-1 之间。
  在讨论优化算法时，老师基本已经不用 sigmoid 激活函数了，tanh 函数在所有场合都优于 sigmoid 函数。但有一个例外：在二分类的问题中，对于输出层，因为的值是 0 或 1，所以想让^的数值介于 0 和 1 之间，而不是在-1 和+1 之间。所以需要使用 sigmoid 激活函数。
  sigmoid 函数和 tanh 函数两者共同的缺点：在特别大或者特别小的情况下，导数的梯度或者函数的斜率会变得特别小，最后就会接近于 0，导致降低梯度下降的速度。
• Relu修正线性单元：$a=max(0,z)$ ，只要是正值的情况下，导数恒等于 1，当是负值的时候，导数恒等于 0。是等于 0 的时候，假设导数是 1 / 0 都可以。
• 选择激活函数的经验法则：
  如果输出是 0、1 值（二分类问题），则输出层选择 sigmoid 函数，其它的所有单元都选择 Relu 函数。
  如果在隐藏层上不确定使用哪个激活函数，那么通常会使用 Relu ，有时也会使用 tanh ，但 Relu的一个优点是：当是负值时导数等于 0。
  还有一个 Leaky Relu，当是负值时，函数值不是等于 0，而是轻微的倾斜，它通常比 Relu 激活函数效果要好，尽管在实际中 Leaky ReLu 使用的并不多。
  

建议：如果不确定哪一个激活函数效果更好，可以把它们都试试，然后在验证集或者发展集上进行评价。然后看哪一种表现的更好，就去使用它。如果仅仅遵守使用默认的ReLu 而不用其他的激励函数，那就可能在近期或者往后，每次解决问题的时候都使用相同的办法。

• 注意一点，我们的激活函数必须是非线性的，这是因为不能在隐藏层使用线性激活函数，唯一可以用线性激活函数的通常就是输出层。原因：事实证明，如果你使用线性激活函数或者没有使用一个激活函数，那么无论你的神经网络有多少层一直在做的只是计算线性函数，所以不如直接去掉全部隐藏层。
• 激活函数的导数：见第三周-3.8节

神经网络-随机初始化权重

当你训练神经网络时，权重随机初始化是很重要的。对于逻辑回归，把权重初始化为 0，当然也是可以的。但是对于一个神经网络，如果你把权重或者参数都初始化为 0，那么梯度下降将不会起作用。

你应该这么做：把 ${}^{[1]}$设为np.random.randn(2,2)(生成高斯分布)，通常再乘上一个小的数，比如 0.01，这样把它初始化为很小的随机数。没有对称的问题（ symmetry breaking problem），所以可以把 初始化为 0，因为只要随机初始化你就有不同的隐含单元计算不同的东西，因此不会有 symmetry breaking 问题了。相似的，对于${}^{[2]}$你可以随机初始化，${}^{[2]}$可以初始化为 0.

你也许会疑惑，这个常数从哪里来，为什么是 0.01，而不是 100 或者 1000。我们通常倾向于初始化为很小的随机数。因为如果你用 tanh 或者 sigmoid 激活函数，如果很大，数值波动太大，就会很大。就会很大或者很小，因此这种情况下你很可能停在tanh/sigmoid 函数的平坦的地方，这些地方梯度很小也就意味着梯度下降会很慢，因此学习也就很慢。

但当你训练一个非常非常深的神经网络，你可能会选择一个不同于的常数而不是 0.01，见下一大块。

深层神经网络

前向传播和反向传播

• 前向传播：
  $z^{[l]}=W^{[l]}\cdot a^{[l-1]}+b^{[l]}$
  $a^{[l]}=g^{[l]}\left(z^{[l]}\right)$
  向量化后：
  $z^{[l]}=W^{[l]}\cdot A^{[l-1]}+b^{[l]}$
  $A^{[l]}=g^{[l]}\left(z^{[l]}\right)$
• 反向传播：
  
  向量化后：
  

核对维数

• 未向量化时：
  W：（下一层的维数，前一层的维数）
  b 、z、a：（下一层的维数，1）
  dw和w维数相同，db和b维数相同，w和b的向量化维度不变，但z、a、x的维度会改变。
• 向量化后：
  
  在做深度神经网络的反向传播时，一定要确认所有的矩阵维数是前后一致的。

用深层表示的意义：

• 可以把这种神经网络的前几层当作探测简单的函数，比如边缘，之后把它们跟后几层结合在一起，那么总体上就能学习更多复杂的函数。
• 这种从简单到复杂的金字塔状表示方法或者组成方法，也可以应用在图像或者人脸识别以外的其他数据上：
  • 比如想要建一个语音识别系统的时候，需要解决的就是如何可视化语音。
    输入一个音频片段，那么神经网络的第一层可能就会去先开始试着探测比较低层次的音频波形的一些特征，比如音调是高是低、分辨白噪音咝咝咝的声音，可以选择这些相对程度比较低的波形特征，然后把这些波形组合在一起就能去探测声音的基本单元。
  • 在语言学中有个概念叫做音位，比如a 的发音“啊”是个音位，t 的发音“特”也是个音位，有了基本的声音单元以后，组合起来，你就能识别音频当中的单词，单词再组合起来就能识别词组，再到完整的句子。
  • Small：隐藏单元的数量相对较少
    Deep：隐藏层数目比较多
  • ，关于神经网络为何有效的理论，来源于电路理论。但是如果你用浅一些的神经网络计算同样的函数，也就是说在我们不能用很多隐藏层时，你会需要成指数增长的单元数量才能达到同样的计算结果。
    

超参数

• 定义：比如算法中的 learning rate （学习率）、iterations(梯度下降法循环的数量)、（隐藏层数目）、[]（隐藏层单元数目）、choice of activation function（激活函数的选择）都需要你来设置，这些数字实际上控制了最后的参数和的值，所以它们被称作超参数。
• 如何确定超参数的值：多试试，观察哪种超参数的组合最好

深度学习和大脑的关联性

总结：毫无关系