吴恩达-deep learning 01.神经网络与深度学习Week3

Week3：浅层神经网络(Shallow neural networks)

3.1 神经网络概述（Neural Network Overview）

本节先从整体结构上来看一下神经网络模型。

• 逻辑回归梯度下降算法——正向传播和反向传播两个过程
  假设某个样本有两个特征$x_1,x_2$，如下图所示：
  
  • 正向传播(黑线)：
    $$\begin{array}{l}z=w^{T}x+b\\ \hat{y}=a=\sigma (z)\\ L(a,y)=-(ylog(a)+(1-y)log(1-a))\end{array}$$
  • 反向传播(红线)：
    第一步：
    $$\begin{array}{l}da=\frac{\partial L}{\partial a}=-\frac{y}{a}+\frac{1-y}{1-a}\\ dz=\frac{\partial L}{\partial z}=\frac{\partial L}{\partial a}\cdot \frac{\partial a}{\partial z}=(-\frac{y}{a}+\frac{1-y}{1-a})\cdot a(1-a)=a-y\end{array}$$
    第二步：知道了$dz$之后，就可以直接对$w_1$，$w_2$和$b$进行求导了。
    $$\begin{array}{l}d{w}_1=\frac{\partial L}{\partial w_1}=\frac{\partial L}{\partial z}\cdot \frac{\partial z}{\partial w_1}=x_1\cdot dz=x_1(a-y)\\ d{w}_2=\frac{\partial L}{\partial w_2}=\frac{\partial L}{\partial z}\cdot \frac{\partial z}{\partial w_2}=x_2\cdot dz=x_2(a-y)\\ db=\frac{\partial L}{\partial b}=\frac{\partial L}{\partial z}\cdot \frac{\partial z}{\partial b}=1\cdot dz=a-y\end{array}$$
    第三步：则梯度下降算法可表示为：
    $$\begin{array}{l}{w}_1:=w_1-\alpha d{w}_1\\ w_2:=w_2-\alpha d{w}_2\\ b:=b-\alpha db\end{array}$$
• 浅层神经网络
  
  • 第一层是从输入层到隐藏层，用上标$[1]$来表示：
    $$\begin{array}{l}{z}^{[1]}=W^{[1]}x+b^{[1]}\\ a^{[1]}=\sigma (z^{[1]})\end{array}$$
  • 第二层是隐藏层到输出层，用上标$[2]$来表示：
    $$\begin{array}{l}{z}^{[2]}=W^{[2]}{a}^{[1]}+b^{[2]}\\ a^{[2]}=\sigma (z^{[2]})\end{array}$$

    $在写法上值得注意的是，方括号上标[i]表示当前所处的层数；圆括号上标(i)表示第i个样本。$
    

简单认为：基于逻辑回归重复使用了两次该模型得到上述例子的神经网络。

---

3.2 神经网络的表示（Neural Network Representation）

本节介绍单隐藏层的神经网络结构。如下图所示，单隐藏层神经网络就是典型的浅层（shallow）神经网络。

• 结构上，从左到右，可以分成三层：输入层（Input layer），隐藏层（Hidden layer） 和 输出层（Output layer）。
  • 输入层和输出层，对应着训练样本的输入和输出。
  • 隐藏层是抽象的非线性的中间层，这也是其被命名为隐藏层的原因。
• 写法上，我们通常把输入矩阵$X$记为$a^{[0]}$，隐藏层输出记为$a^{[1]}$，输出层记为$a^{[2]}$，即$\hat{y}$。
  • 上标表示第几层，上标从0开始。
  • 下标表示第几个神经元，下标从1开始。
    • 例如$a_1^{[1]}$表示隐藏层第1个神经元，$a_2^{[1]}$表示隐藏层第2个神经元。隐藏层有4个神经元就可以将其输出$a^{[1]}$写成矩阵的形式：
      $$a^{[1]}=\left[\begin{array}{c}{a}_1^{[1]}\\ a_2^{[1]}\\ a_3^{[1]}\\ a_4^{[1]}\end{array}\right]$$
  • 这种单隐藏层神经网络也被称为两层神经网络（2 layer NN）。

    通常我们只会计算隐藏层输出和输出层的输出，输入层是不用计算的。这也是我们把输入层层数上标记为0的原因（a^{[0]}）。

• 权重$W$和常数项$b$：
  • 隐藏层对应的权重$W^{[1]}$和常数项$b^{[1]}$：
    • $W^{[1]}$的维度是$(4,3)$。这里的4对应着隐藏层神经元个数，3对应着输入层x特征向量包含元素个数。
    • 常数项$b^{[1]}$的维度是$(4,1)$，这里的4同样对应着隐藏层神经元个数。
  • 输出层对应的权重$W^{[2]}$和常数项$b^{[2]}$：
    • $W^{[2]}$的维度是$(1,4)$，这里的1对应着输出层神经元个数，4对应着输出层神经元个数。
    • 常数项$b^{[2]}$的维度是$(1,1)$，因为输出只有一个神经元。

  总结一下：第$i$层的权重$W^{[i]}$维度的行等于$i$层神经元的个数，列等于$i-1$层神经元的个数；第$i$层常数项$b^{[i]}$维度的行等于$i$层神经元的个数，列始终为$1$。

---

3.3 计算一个神经网络的输出（Computing a Neural Network’s output）

本节从一个样本数据（有三个特征($x_1,x_2,x_3$)，每个特征一个维度）为例，了解神经网络的输出究竟是如何计算出来的。

• 计算$z$和$a$：
  

  对于上图右边的两层神经网络，从输入层到隐藏层对应一次逻辑回归运算；从隐藏层到输出层对应一次逻辑回归运算。每层计算时，要注意对应的上标和下标，一般我们记上标方括号表示layer，下标表示第几个神经元。例如$a_i^{[l]}$表示第l层的第$i$个神经元。注意，$i$从1开始，$l$从0开始。

  • 对于逻辑回归：
    小圆圈代表了计算的两个步骤。
    • 第一步，计算$z_1^{[1]},z_1^{[1]}=w_1^{[1]T}x+b_1^{[1]}$。
    • 第二步，通过激活函数计算$a_1^{[1]},a_1^{[1]}=\sigma (z_1^{[1]})$。
  • 对于两层神经网络：
    • 输入层到隐藏层：
      $$\begin{array}{l}{z}_1^{[1]}=w_1^{[1]T}x+b_1^{[1]},a_1^{[1]}=\sigma (z_1^{[1]})\\ z_2^{[1]}=w_2^{[1]T}x+b_2^{[1]},a_2^{[1]}=\sigma (z_2^{[1]})\\ z_3^{[1]}=w_3^{[1]T}x+b_3^{[1]},a_3^{[1]}=\sigma (z_3^{[1]})\\ z_4^{[1]}=w_4^{[1]T}x+b_4^{[1]},a_4^{[1]}=\sigma (z_4^{[1]})\end{array}$$
    • 隐藏层到输出层：
      $$z_1^{[2]}=w_1^{[2]T}{a}^{[1]}+b_1^{[2]},a_1^{[2]}=\sigma (z_1^{[2]})$$
• 向量化计算
  为了提高程序运算速度，我们引入向量化和矩阵运算的思想，将上述表达式转换成矩阵运算的形式：
  
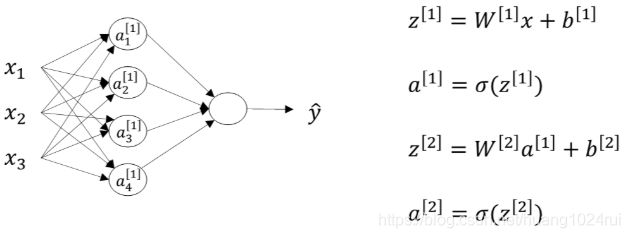
  • 形式为：
    $$\begin{array}{l}{z}^{[1]}=W^{[1]}x+b^{[1]}\\ a^{[1]}=\sigma (z^{[1]})\\ z^{[2]}=W^{[2]}{a}^{[1]}+b^{[2]}\\ a^{[2]}=\sigma (z^{[2]})\end{array}$$

    $W^{[1]}$的维度是$(4,3)$，$b^{[1]}$的维度是$(4,1)$，$W^{[2]}$的维度是$(1,4)$，$b^{[2]}$的维度是$(1,1)$。

    • 其中：
      $$\left[\begin{array}{c}{z}_1^{[1]}\\ z_2^{[1]}\\ z_3^{[1]}\\ z_4^{[1]}\end{array}\right]=\stackrel{W^{[1]}}{\left[\begin{array}{c}...W_1^{[1]T}...\\ ...W_2^{[1]T}...\\ ...W_3^{[1]T}...\\ ...W_4^{[1]T}...\end{array}\right]}\ast \stackrel{input}{\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right]}+\stackrel{b^{[1]}}{\left[\begin{array}{c}{b}_1^{[1]}\\ b_2^{[1]}\\ b_3^{[1]}\\ b_4^{[1]}\end{array}\right]}$$
      $$a^{[1]}=\left[\begin{array}{c}{a}_1^{[1]}\\ a_2^{[1]}\\ a_3^{[1]}\\ a_4^{[1]}\end{array}\right]=\sigma (z^{[1]})$$

---

3.4 多样本向量化（Vectorizing across multiple examples）

上一节了解到如何对单一的训练样本($x$维度为$n_x$)，在神经网络上计算预测值。本节将会了解如何向量化多个训练样本($m$个$n_x$维度的训练样本$x^{(1)}...x^{(m)}$)，并计算出结果。

• 循环形式：
  书写标记上用上标$(i)$表示第$i$个样本，例如$x^{(i)}，z^{(i)}，a^{[2](i)}$。对于每个样本$i$，可以使用for循环来求解其正向输出：
  $$\begin{array}{l}fori=1tom:\\ z^{[1](i)}=W^{[1]}{x}^{(i)}+b^{[1]}\\ a^{[1](i)}=\sigma (z^{[1](i)})\\ z^{[2](i)}=W^{[2]}{a}^{[1](i)}+b^{[2]}\\ a^{[2](i)}=\sigma (z^{[2](i)})\end{array}$$
• 矩阵形式：
  • 对各数据的向量化：
    • $$X=\left[\begin{array}{cccc}⋮& ⋮& ⋮& ⋮\\ x^{(1)}& x^{(2)}& \cdots & x^{(m)}\\ ⋮& ⋮& ⋮& ⋮\end{array}\right]$$
    • $$Z^{[1]}=\left[\begin{array}{cccc}⋮& ⋮& ⋮& ⋮\\ z^{[1](1)}& z^{[1](2)}& \cdots & z^{[1](m)}\\ ⋮& ⋮& ⋮& ⋮\end{array}\right]$$
    • $$A^{[1]}=\left[\begin{array}{cccc}⋮& ⋮& ⋮& ⋮\\ {\alpha }^{[1](1)}& {\alpha }^{[1](2)}& \cdots & {\alpha }^{[1](m)}\\ ⋮& ⋮& ⋮& ⋮\end{array}\right]$$
  • 整体矩阵化：
    $$\begin{array}{r}\text{z[1](i)=W[1](i)x(i)+b[1]}\\ \text{α[1](i)=σ(z[1](i))}\\ \text{z[2](i)=W[2](i)α[1](i)+b[2]}\\ \text{α[2](i)=σ(z[2](i))}\end{array}\}⟹\{\begin{array}{l}\text{Z[1]=W[1]X+b[1]}\\ \text{A[1]=σ(Z[1])}\\ \text{Z[2]=W[2]A[1]+b[2]}\\ \text{A[2]=σ(Z[2])}\end{array}$$

    其中，$Z^{[1]}$的维度是$(4,m)$，4是隐藏层神经元的个数；$A^{[1]}$的维度与$Z^{[1]}$相同；$Z^{[2]}$和$A^{[2]}$的维度均为$(1,m)$。对上面这四个矩阵来说，均可以这样来理解：行表示神经元个数，列表示样本数目m。

• 对于矩阵化各数据的进一步解读：
  • $a_j^{[1](i)}$与$A$；$z^{[1](i)}$与$Z$：
    • 在垂直方向，对应的是$a_j^{[1]}$中的$j$，这个垂直索引对应于神经网络中的不同节点。
    • 在水平方向，对应的是$a^{[1](i)}$中的$i$，矩阵$A$代表了各个训练样本。
    • 当垂直扫描，是索引隐藏单位的数字。
    • 当水平扫描，是索引$m$个训练样本中的某一个训练样本。

---

3.5 向量化实现的解释（Justification for vectorized implementation）

本节只是对上一节的矩阵化(向量化)做进一步的解释。

• 假设有$m$个样本($x^{[1]}，x^{[2]}，x^{[3]}$)，
  • 则对于隐藏层，可以写成：
    $$\begin{gathered} z^{[1](1)}=W^{[1]}{x}^{(1)}+b^{[1]} \\ {z}^{[1](2)}=W^{[1]}{x}^{(2)}+b^{[1]} \\ {z}^{[1](3)}=W^{[1]}{x}^{(3)}+b^{[1]} \end{gathered}$$
  • 由于Python 的广播机制，可以很容易的将$b^{[1]}$ 加进来，因此在这先忽略$b^{[1]}$ 。
    $$\begin{array}{rl}& Z^{[1]}=W^{[1]}X=\left[\begin{array}{c}\cdots \\ \cdots \\ ⋮\\ \cdots \end{array}\right]\left[\begin{array}{cccc}⋮& ⋮& ⋮& ⋮\\ x^{(1)}& x^{(2)}& x^{(3)}& ⋮\\ ⋮& ⋮& ⋮& ⋮\end{array}\right]=\left[\begin{array}{cccc}⋮& ⋮& ⋮& ⋮\\ w^{(1)}{x}^{(1)}& w^{(1)}{x}^{(2)}& w^{(1)}{x}^{(3)}& ⋮\\ ⋮& ⋮& ⋮& ⋮\end{array}\right]\\ & \left[\begin{array}{cccc}⋮& ⋮& ⋮& ⋮\\ z^{[1](1)}& z^{[1](2)}& z^{[1](3)}& ⋮\\ ⋮& ⋮& ⋮& ⋮\end{array}\right]\end{array}$$
    具体分析跟上一节类似，就不在这赘述了。

---

3.6 激活函数（Activation functions）

神经网络隐藏层和输出层都需要激活函数（activation function），在之前的课程中我们都默认使用Sigmoid函数$\sigma (x)$作为激活函数。其实，还有其它激活函数可供使用，不同的激活函数有各自的优点。

• 几个不同的激活函数g(x)：
  • sigmoid函数：
    
  • tanh函数：
  • ReLU函数(线性整流函数（Rectified Linear Unit))：
    
  • Leaky ReLU函数：
    
• 激活函数的解释：
  • sigmoid激活函数：除了输出层是一个二分类问题基本不会用它。
  • tanh激活函数：tanh是非常优秀的，几乎适合所有场合。
  • ReLu激活函数：最常用的默认函数，如果不确定用哪个激活函数，就使用ReLu或者Leaky ReLu，保证梯度下降速度不会太小。
  • 具体选择哪个函数作为激活函数没有一个固定的准确的答案，应该要根据具体实际问题进行验证（validation）。

---

3.7 为什么需要非线性激活函数？（why need a nonlinear activation function?）

上一节讲的四种激活函数都是**非线性(non-linear)**的。那是否可以使用线性激活函数呢？我们从两个方面来讨论。

• 一方面：假设所有的激活函数都是线性的，我们直接令激活函数$g(z)=z$，即$a=z$；根据浅层神经网络，我们可以得到：
  $$\begin{array}{l}{z}^{[1]}=W^{[1]}x+b^{[1]}\\ a^{[1]}=z^{[1]}\\ z^{[2]}=W^{[2]}{a}^{[1]}+b^{[2]}\\ a^{[2]}=z^{[2]}\end{array}$$
  我们对上式中$a^{[2]}$进行化简计算：
  $$a^{[2]}=z^{[2]}=W^{[2]}{a}^{[1]}+b^{[2]}=W^{[2]}(W^{[1]}x+b^{[1]})+b^{[2]}=(W^{[2]}{W}^{[1]})x+(W^{[2]}{b}^{[1]}+b^{[2]})=W’x+b’$$
  发现$a^{[2]}$仍是输入变量$x$的线性组合，与使用神经网络与直接使用线性模型的效果并没有什么两样。因此，隐藏层的激活函数必须要是非线性的。
• 另一方面：神经网络模拟人的神经元，人的每个神经元也是要受到一定强度的刺激，才能工作。这种刺激，一般也是非线性，正好契合隐藏层的激活函数需要是非线性的。

---

3.8 激活函数的导数（Derivatives of activation functions）

在神经网络中使用反向传播的时候，你真的需要计算激活函数的斜率或者导数。针对以下四种激活，求其导数如下：

1. sigmoid activation function
   

   • $\frac{d}{dz}g(z)=\frac{1}{1+e^{-z}}(1-\frac{1}{1+e^{-z}})=g(z)(1-g(z))$

   • 注：

     • 当$z=10$ ; $\frac{d}{dz}g(z)\approx 0$
     • 当$z=-10$ ; $\frac{d}{dz}g(z)\approx 0$
     • 当$z=0$ ； $\frac{d}{dz}g(z)\text{=g(z)(1-g(z))=}1/4$

   在神经网络中$a=g(z)$; $g{(z)}^{{}^{\prime }}=\frac{d}{dz}g(z)=a(1-a)$

2. Tanh activation function
   

   • $g(z)=tanh(z)=\frac{e^z-e^{-z}}{e^z+e^{-z}}$
     $\frac{d}{dz}g(z)=1-(tanh(z){)}^2$
   • 注：
     • 当$z$ = 10； $\frac{d}{dz}g(z)\approx 0$
     • 当$z=-10$； $\frac{d}{dz}g(z)\approx 0$
     • 当$z$ = 0； $\frac{d}{dz}g(z)\text{=1-(0)=}1$

3. Rectified Linear Unit (ReLU)
   

   • $g(z)=max(0,z)$
   • $$g(z{)}^{{}^{\prime }}=\{\begin{array}{ll}0& \text{if z < 0}\\ 1& \text{if z > 0}\\ undefined& \text{if z = 0}\end{array}$$

   注：通常在$z$= 0的时候给定其导数1,0；当然$z$=0的情况很少

4. Leaky linear unit (Leaky ReLU)
   

   • $$g(z)=\max (0.01z,z)$$
   • $$g(z{)}^{{}^{\prime }}=\{\begin{array}{ll}0.01& \text{if z < 0}\\ 1& \text{if z > 0}\\ undefined& \text{if z = 0}\end{array}$$

   注：通常在$z=0$的时候给定其导数1,0.01；当然$z=0$的情况很少。

---

3.9 神经网络的梯度下降（Gradient descent for neural networks）

1. 对于浅层神经网络，假设包含的参数为$W^{[1]}，b^{[1]}，W^{[2]}，b^{[2]}$。

   • 令输入层的特征向量个数$n_x=n^{[0]}$，隐藏层神经元个数为$n^{[1]}$，输出层神经元个数为$n^{[2]}=1$。
   • 则$W^{[1]}$的维度为$(n^{[1]},n^{[0]})$，$b^{[1]}$的维度为$(n^{[1]},1)$，W^{[2]}的维度为$(n^{[2]},n^{[1]})$，$b^{[2]}$的维度为$(n^{[2]},1)$。
     

2. forward propagation：
   $$\begin{array}{l}{Z}^{[1]}=W^{[1]}X+b^{[1]}-----(3.9.1.1)\\ A^{[1]}=\sigma (Z^{[1]})--------(3.9.1.2)\\ Z^{[2]}=W^{[2]}{A}^{[1]}+b^{[2]}-----(3.9.1.3)\\ A^{[2]}=\sigma (Z^{[2]})--------(3.9.1.4)\end{array}$$

3. back propagation：
   利用分步求导法则：
   $$\begin{array}{l}d{Z}^{[2]}=A^{[2]}-Y,Y=\left[\begin{array}{cccc}{y}^{[1]}& y^{[2]}& \cdots & y^{[m]}\end{array}\right]--------(3.9.2.1)\\ d{W}^{[2]}=\frac{1}{m}d{Z}^{[2]}{A}^{[1]T}------------------(3.9.2.2)\\ \mathrm{d}{b}^{[2]}=\frac{1}{m}np.sum(d{Z}^{[2]},axis=1,keepdims=True)----(3.9.2.3)\\ d{Z}^{[1]}=W^{[2]T}\mathrm{d}{Z}^{[2]}{g}^{{[1]}^{{}^{\prime }}}(Z^{[1]})---------------(3.9.2.4)\\ d{W}^{[1]}=\frac{1}{m}d{Z}^{[1]}{x}^T-------------------(3.9.2.5)\\ d{b}^{[1]}=\frac{1}{m}np.sum(d{Z}^{[1]},axis=1,keepdims=True)----(3.9.2.6)\end{array}$$

   注：1.其中$d{z}^{[1]}$为：
   $$d{Z}^{[1]}=\underset{(n^{[1]},m)}{W^{[2]T}\mathrm{d}{Z}^{[2]}}\ast \underset{activationfunctionofhiddenlayer}{{g^{[1]}}^{{}^{\prime }}}\ast \underset{(n^{[1]},m)}{(Z^{[1]})}$$
   2. 其中$d{b}^{[1]}$为：
   $$\underset{(n^{[1]},1)}{d{b}^{[1]}}=\frac{1}{m}np.sum(d{Z}^{[1]},axis=1,keepdims=True)$$
   3. 这些都是针对所有样本进行过向量化，$Y$是$1\times m$的矩阵；这里np.sum是python的numpy命令，axis=1表示水平相加求和，keepdims是防止python输出那些古怪的秩数$(n,)$，加上这个确保阵矩阵$d{b}^{[2]}$这个向量输出的维度为$(n,1)$这样标准的形式。

---

3.10（选修）直观理解反向传播（Backpropagation intuition）

我们先回顾逻辑回归的推导，再看看浅层神经网络反向传播的推到。

1. 逻辑回归
   
   • 正向：
     $$\begin{array}{l}x\\ w\\ b\end{array}\}⟹z=w^{T}x+b⟹\alpha =\sigma (z)⟹L\left(a,y\right)---(3.10.1)$$
   • 反向：
     $$\underset{dw=dz\cdot x,db=dz}{\begin{array}{l}x\\ w\\ b\end{array}\}}⟸\underset{dz=da\cdot g^{{}^{\prime }}(z),g(z)=\sigma (z),\frac{dL}{dz}=\frac{dL}{da}\cdot \frac{da}{dz},\frac{d}{dz}g(z)=g^{{}^{\prime }}(z)}{z=w^{T}x+b}⟸\underset{da=\frac{d}{da}L\left(a,y\right)=(-y\log \alpha -(1-y)\log (1-a){)}^{{}^{\prime }}=-\frac{y}{a}+\frac{1-y}{1-a}}{a=\sigma (z)⟸L(a,y)}--(3.10.2)$$
2. 浅层神经网络
   

   • 反向传播(红色)

     • 对单个样本的数学公式
       $$\begin{array}{l}d{z}^{[2]}=a^{[2]}-y------(3.10.1)\\ d{W}^{[2]}=d{z}^{[2]}\cdot \frac{\partial z^{[2]}}{\partial W^{[2]}}=d{z}^{[2]}{a}^{[1]T}------(3.10.2)\\ d{b}^{[2]}=d{z}^{[2]}\cdot \frac{\partial z^{[2]}}{\partial b^{[2]}}=d{z}^{[2]}\cdot 1=d{z}^{[2]}------(3.10.3)\\ d{z}^{[1]}=d{z}^{[2]}\cdot \frac{\partial z^{[2]}}{\partial a^{[1]}}\cdot \frac{\partial a^{[1]}}{\partial z^{[1]}}=W^{[2]T}d{z}^{[2]}\ast g^{[1]’}(z^{[1]})------(3.10.4)\\ d{W}^{[1]}=d{z}^{[1]}\cdot \frac{\partial z^{[1]}}{\partial W^{[1]}}=d{z}^{[1]}{x}^T------(3.10.5)\\ d{b}^{[1]}=d{z}^{[1]}\cdot \frac{\partial z^{[1]}}{\partial b^{[1]}}=d{z}^{[1]}\cdot 1=d{z}^{[1]}------(3.10.6)\end{array}$$

     $Z^{[1]}=W^{[1]}x+b^{[1]},a^{[1]}=g^{[1]}(Z^{[1]})$得到：$$Z^{[1]}=\left[\begin{array}{cccc}⋮& ⋮& ⋮& ⋮\\ z^{[1](1)}& z^{[1](2)}& ⋮& z^{[1](m)}\\ ⋮& ⋮& ⋮& ⋮\end{array}\right]$$
     大写的$Z^{[1]}$表示$z^{[1](1)},z^{[1](2)},z^{[1](3)}...z^{[1](m)}$的列向量堆叠成的矩阵，以下类同。

     • 对多个样本的Python语言(如上一节的‘公式3.9.2‘)
       $$\begin{array}{l}d{Z}^{[2]}=A^{[2]}-Y,Y=\left[\begin{array}{cccc}{y}^{[1]}& y^{[2]}& \cdots & y^{[m]}\end{array}\right]\\ d{W}^{[2]}=\frac{1}{m}d{Z}^{[2]}{A}^{[1]T}\\ \mathrm{d}{b}^{[2]}=\frac{1}{m}np.sum(d{Z}^{[2]},axis=1,keepdims=True)\\ d{Z}^{[1]}=W^{[2]T}\mathrm{d}{Z}^{[2]}{g}^{{[1]}^{{}^{\prime }}}(Z^{[1]})\\ d{W}^{[1]}=\frac{1}{m}d{Z}^{[1]}{x}^T\\ d{b}^{[1]}=\frac{1}{m}np.sum(d{Z}^{[1]},axis=1,keepdims=True)\end{array}$$

---

3.11 随机初始化（Random+Initialization）

1. 对称问题（symmetry breaking problem）
   一个浅层神经网络包含两个输入，隐藏层包含两个神经元。如果权重W^{[1]}和W{[2]}都初始化为零: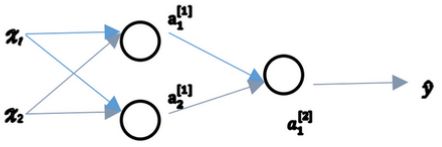
   $$\begin{array}{l}{W}^{[1]}=\left[\begin{array}{ll}0& 0\\ 0& 0\end{array}\right]W^{[2]}=\left[\begin{array}{ll}0& 0\end{array}\right]\end{array}$$
   • 这样使得隐藏层第一个神经元的输出等于第二个神经元的输出，即$a_1^{[1]}=a_2^{[1]}$。经过推导得到$d{z}_1^{[1]}=d{z}_2^{[1]}$，以及$d{W}_1^{[1]}=d{W}_2^{[1]}$。
   • 隐藏层两个神经元对应的权重行向量$W_1^{[1]}$和$W_2^{[1]}$每次迭代更新都会得到完全相同的结果，$W_1^{[1]}$始终等于$W_2^{[1]}$，完全对称。这样隐藏层设置多个神经元就没有任何意义了。
   • 参数$b$可以全部初始化为零，并不会影响神经网络训练效果。
   • 把这种权重$W$全部初始化为零带来的问题称为symmetry breaking problem。
2. 解决方法
   python里可以使用如下语句进行W和b的初始化：

   W_1 = np.random.randn((2,2))*0.01
   b_1 = np.zero((2,1))
   W_2 = np.random.randn((1,2))*0.01
   b_2 = 0
   

   • 将$W_1^{[1]}$和$W_2^{[1]}$乘以0.01的目的是尽量使得权重$W$初始化比较小的值。之所以让$W$比较小，是因为如果使用$sigmoid$函数或者$tanh$函数作为激活函数的话，$W$比较小，得到的$|z|$也比较小（靠近零点），而零点区域的梯度比较大，这样能大大提高梯度下降算法的更新速度，尽快找到全局最优解。

   如果激活函数是ReLU或者Leaky ReLU函数，则不需要考虑这个问题。

---

本章总结

• 左上： 浅层网络即隐藏层数较少，如图所示，这里仅有一个隐藏层。
• 左下： 这里介绍了不同激活函数的特点：
  • sigmoid：sigmoid 函数常用于二分分类问题，或者多分类问题的最后一层，主要是由于其归一化特性。sigmoid 函数在两侧会出现梯度趋于零的情况，会导致训练缓慢。
  • tanh：相对于 sigmoid，tanh 函数的优点是梯度值更大，可以使训练速度变快。
  • ReLU：可以理解为阈值激活（spiking model 的特例，类似生物神经的工作方式），该函数很常用，基本是默认选择的激活函数，优点是不会导致训练缓慢的问题，并且由于激活值为零的节点不会参与反向传播，该函数还有稀疏化网络的效果。
  • Leaky ReLU：避免了零激活值的结果，使得反向传播过程始终执行，但在实践中很少用。
• 右上：为什么要使用激活函数呢？更准确地说是，为什么要使用非线性激活函数呢？
  上图中的实例可以看出，没有激活函数的神经网络经过两层的传播，最终得到的结果和单层的线性运算是一样的，也就是说，没有使用非线性激活函数的话，无论多少层的神经网络都等价于单层神经网络（不包含输入层）。
• 右下：如何初始化参数 w、b 的值？
  当将所有参数初始化为零的时候，会使所有的节点变得相同，在训练过程中只能学到相同的特征，而无法学到多层级、多样化的特征。解决办法是随机初始化所有参数，但仅需少量的方差就行，因此使用 Rand*(0.01)进行初始化，其中 0.01 也是超参数之一。