概率图模型
文章目录
-
- 9.1 有向图模型：贝叶斯网络
- 9.2 无向图模型：马尔科夫随机场
- 9.3 学习与推断
- 9.5 实例模型
9.1 有向图模型：贝叶斯网络
图结构：有向无环图（DAG）
结点：一个或一组随机变量
边：随机变量之间的单向、直接影响
条件独立性：D-分离准则：判断贝叶斯网络结点之间的条件独立性
贝叶斯网络的全局马尔可夫性：给定结点集合A,B,C，若A到B中结点的所有无向路径都是被C阻塞的，则称A和B是被C D-分离的，即A和B关于C条件独立。
阻塞的:若一条无向路径包含结点x满足以下条件之一，则称其是阻塞的：
（1）x是tail-to-tail或head-to-tail结点，并且x包含在C中
（2）x是head-to-head结点，并且x(及其x的任意后代均)不包含在C中
贝叶斯网络的局部马尔可夫性：
（1）给定某变量的父结点，则该变量条件独立于所有其他非其后代结点
（2）给定某变量的马尔可夫毯（父结点、子结点、子结点的父结点），则改变了条件独立于其他变量
9.2 无向图模型：马尔科夫随机场
图结构：无向图
结点：一个或一组随机变量
边：随机变量之间的相互依赖（非“因果关系”）
团：对于图中的结点子集，若其中任意两个结点之间都有连边，则称该节点子集为一个团
极大团：若在团中加入其他任意一个结点都不再形成团，则称该团为极大团
马尔可夫随机场的全局马尔可夫性：给定结点集合A,B,C，若从A中的结点到B中结点必须经过C中的结点，则称A和B被C分离，即A和B关于C条件独立
局部马尔可夫性：给定某变量的马尔可夫毯（邻接变量），则该变量条件独立于其他变量
成对马尔可夫性：给定其他所有变量，两个非相邻变量条件独立
9.3 学习与推断
推断：已知联合概率分布 P ( x 1 , x 2 , . . . , x n ) P(x_{1},x_{2},...,x_{n}) P(x1,x2,...,xn)，估计 P ( x Q ∣ x E ) P(x_{Q}|x_{E}) P(xQ∣xE)，其中 x Q ∩ x E = ϕ x_{Q}\cap x_{E}=\phi xQ∩xE=ϕ， x Q ∪ x E x_{Q}\cup x_{E} xQ∪xE是集合 { x 1 , x 2 , . . . , x n } \{x_{1},x_{2},...,x_{n} \} {x1,x2,...,xn}的子集， x Q x_{Q} xQ是问题变量， x E x_{E} xE是证据变量。
P ( x Q ∣ x E ) = P ( x Q , x E ) P ( x E ) = P ( x Q , x E ) ∑ x Q P ( x Q , x E ) P(x_{Q}|x_{E})=\frac{P(x_{Q},x_{E})}{P(x_{E})}=\frac{P(x_{Q},x_{E})}{\sum_{x_{Q}}P(x_{Q},x_{E})} P(xQ∣xE)=P(xE)P(xQ,xE)=∑xQP(xQ,xE)P(xQ,xE)
核心问题： ∑ x Q P ( x Q , x E ) \sum_{x_{Q}}P(x_{Q},x_{E}) ∑xQP(xQ,xE)
枚举：假设 x Q x_{Q} xQ有k个变量，每个变量的取值个数的期望是r，则时间复杂度为 r k r^{k} rk
推断的核心问题：如何高效地计算边际分布 P ( x E ) = ∑ x Q P ( x Q , x E ) P(x_{E})=\sum_{x_{Q}}P(x_{Q},x_{E}) P(xE)=∑xQP(xQ,xE)
推断方法：
-
精确推断：计算 P ( x E ) P(x_{E}) P(xE)或 P ( x Q ∣ x E ) P(x_{Q}|x_{E}) P(xQ∣xE)的精确值
- 计算复杂度随着极大团规模的增长呈指数级增长，适用范围有限
- （1）变量消去
- 利用图模型的紧凑概率分布形式来削减计算量
- 优点：简单直观，代数上的消去对应图中结点的消去
- 缺点：针对不同的证据变量会造成大量的冗余计算
- （2）信念传播
- 将变量消去过程中产生的中间结果视为可复用的消息，避免重复计算
-
近似推断：在较低的时间复杂度下获得原问题的近似解
-
通过采样一组服从特定分布的样本，来近似原始分布，适用范围更广，操作性更强
-
（1）前向采样
- 依据贝叶斯网络（条件）概率直接采样
- 缺点：
- 对小概率事件采样困难，可能经过很多次采样也无法获得足够多的样本
- 仅适用于贝叶斯网络，不适用于马尔可夫随机场
-
（2）吉布斯采样
- 直接依照条件概率 P ( x Q ∣ x E ) P(x_{Q}|x_{E}) P(xQ∣xE)采样
- 优点：
- 直接从 P ( x Q ∣ x E ) P(x_{Q}|x_{E}) P(xQ∣xE)采样，解决小概率事件采样难的问题
- 同时适用于贝叶斯网络和马尔可夫随机场
- 简单易推导，时间复杂度低
-
学习：从观测数据 x ( 1 ) , x ( 2 ) , . . . , x ( m ) x^{(1)},x^{(2)},...,x^{(m)} x(1),x(2),...,x(m)中学习联合概率分布 P ( x 1 , x 2 , . . . , x n ) P(x_{1},x_{2},...,x_{n}) P(x1,x2,...,xn)，寻找最符合观测数据的概率图模型
9.4 近似推断
9.5 实例模型
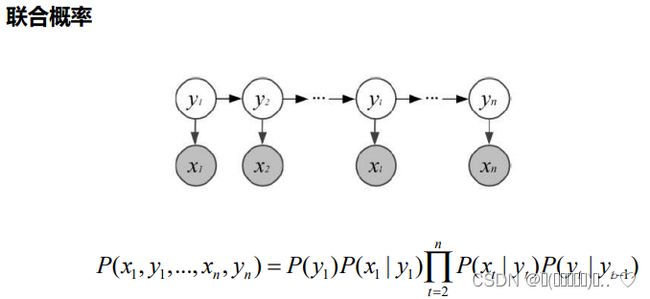
隐马尔可夫模型HMM
定义：隐马尔科夫模型是关于时序的概率模型，是最简单的动态贝叶斯网络模型
状态变量 { y 1 , y 2 , . . . , y n } , y t ϵ Y \{y_{1},y_{2},...,y_{n} \}, y_{t}\epsilon Y {y1,y2,...,yn},ytϵY表示第t时刻的系统状态
观测变量 { x 1 , x 2 , . . . , x n } , x t ϵ X \{x_{1},x_{2},...,x_{n} \}, x_{t}\epsilon X {x1,x2,...,xn},xtϵX表示第t时刻的观测值
观测变量仅依赖于当前时刻的状态变量，当前状态仅依赖于前一时刻的状态
状态集合 Y = { s 1 , s 2 , . . . , s N } Y=\{s_{1},s_{2},...,s_{N} \} Y={s1,s2,...,sN}，观测值集合 X = { o 1 , o 2 , . . . , o M } X=\{o_{1},o_{2},...,o_{M} \} X={o1,o2,...,oM}
隐马尔可夫模型由A，B， π \pi π唯一确定，三者称为隐马尔可夫模型的三要素
生成过程：给定A,B, π \pi π，生成观测序列 { x 1 , x 2 , . . . , x n } \{x_{1},x_{2},...,x_{n} \} {x1,x2,...,xn}
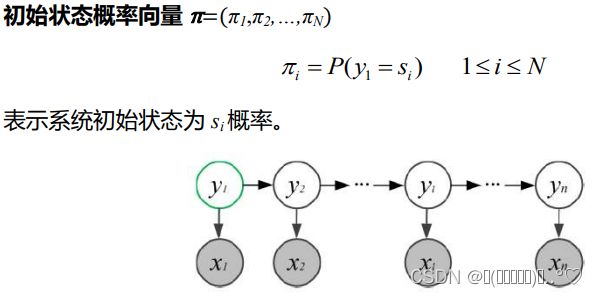
(1)设置t=1，并根据初始状态概率 π \pi π生成初始状态 y 1 y_{1} y1
(2)根据 y t y_{t} yt和观测概率矩阵B生成 x t x_{t} xt
(3)根据 y t y_{t} yt和状态转移矩阵A生成 y t + 1 y_{t+1} yt+1
(4)若t 三个基本问题： （1）概率计算问题：给定模型 λ = ( A , B , π ) \lambda=(A,B,\pi) λ=(A,B,π)和观测序列 x = { x 1 , x 2 , . . . , x n } x=\{x_{1},x_{2},...,x_{n} \} x={x1,x2,...,xn}，计算在模型 λ \lambda λ下观测到x的概率 P ( x ∣ λ ) P(x|\lambda) P(x∣λ)（评估模型与观测序列之间的匹配程度） （2）预测问题：给定模型 λ = ( A , B , π ) \lambda=(A,B,\pi) λ=(A,B,π)和观测序列 x = { x 1 , . . . , x n } x=\{x_{1},...,x_{n} \} x={x1,...,xn}，求使得条件概率 P ( y ∣ x , λ ) P(y|x,\lambda) P(y∣x,λ)最大的观测序列 y = { y 1 , . . . , y n } y=\{y_{1},...,y_{n} \} y={y1,...,yn}（根据观测序列推测状态序列） （3）学习问题：给定观测序列 x = { x 1 , . . . , x n } x=\{x_{1},...,x_{n} \} x={x1,...,xn}，调整模型 λ = ( A , B , π ) \lambda=(A,B,\pi) λ=(A,B,π)参数，使得该系列出现的概率 P ( x ∣ λ ) P(x|\lambda) P(x∣λ)最大（训练模型使其更好地描述观测序列） 条件随机场CRF 定义：条件随机场是给定随机变量x的条件下，随机变量y的马尔可夫随机场。G(V,E)是y中的随机变量构成的无向图，图中每个变量在给定条件x条件下都满足马尔可夫性