常用损失函数及其应用场景
文章目录
- 1 Regression
-
- 1.1 均方误差(MSE)/L2损失
- 1.2 均方根误差(root mean suqare error,RMSE)
- 1.3 平均绝对误差MAE/L1损失
- 1.4 平均偏差误差(Mean Bias Error)
- 1.5 平均绝对百分比误差(Mean Absolute Pencent Error,MAPE)
- 1.6 Huber损失函数
- 2 Classification
-
- 2.1 0-1损失函数(zero-one loss)——Perception
- 2.2 对数损失函数(log)——LR
- 2.3 指数损失函数——Adaboost
- 2.4 Hinge损失——SVM
- 2.5 交叉熵损失函数——LR
- 2.6 对数损失和极大似然函数的关系
在机器学习中,主要有两大任务,分别是分类和回归任务,下面针对这两大场景分别介绍常用的损失函数。
损失函数一般使用 L ( y , f ( x ) ) L(y,f(x)) L(y,f(x))表示,代表预测值和实际值的偏差程度,一般是追求越小越好。
此外,再看一些定义:
- 损失函数:用于衡量’单个样本点’预测值与实际值的偏离程度。
- 风险函数:训练过程中的模型,对已知训练数据的计算。可以理解为是train过程的loss。用于衡量’样本点平均意义’下的好坏,就是说要除以batch_size。
- 经验风险:指预测结果和实际结果的差别。
- 结构风险:指经验风险 + 正则项。
- 泛化函数:指模型对未知数据的预测能力。训练好的模型,对未知数据的计算。可以理解为是test过程的loss。
1 Regression
在回归任务中,预测值和实际值都是实数,一般采用残差 y − f ( x ) y-f(x) y−f(x) 来度量两者的不一致程度.。
1.1 均方误差(MSE)/L2损失
顾名思义,均方误差(MSE)度量的是预测值和实际观测值间差的平方的均值。它只考虑误差的平均大小,不考虑其方向。
- 经过平方,与真实值偏离较多的预测值会受到更为严重的惩罚,所以不够robust。
- MSE 的数学特性很好,这使得计算梯度变得更容易。
M S E = 1 2 n ∑ ( y i − y ^ i ) 2 MSE=\frac{1}{2n}\sum\left(y_{i}-\hat{y}_{i}\right)^{2} MSE=2n1∑(yi−y^i)2
进一步也可以演变为均方根误差函数。
1.2 均方根误差(root mean suqare error,RMSE)
R M S E = ∑ i = 0 n ( y i − y ^ i ) 2 n R M S E=\sqrt{\frac{\sum_{i=0}^{n}\left(y_{i}-\hat{y}_{i}\right)^{2}}{n}} RMSE=n∑i=0n(yi−y^i)2
1.3 平均绝对误差MAE/L1损失
和 MSE 一样,这种度量方法也是在不考虑方向的情况下衡量误差大小。
- MAE 需要像线性规划这样更复杂的工具来计算梯度。
- MAE 对异常值更加稳健,因为它不使用平方。
M A E = ∑ i = 1 n ∣ y i − y ^ i ∣ n M A E=\frac{\sum_{i=1}^{n}\left|y_{i}-\hat{y}_{i}\right|}{n} MAE=n∑i=1n∣yi−y^i∣
1.4 平均偏差误差(Mean Bias Error)
与其它损失函数相比,这个函数在机器学习领域没有那么常见。它与 MAE 相似,唯一的区别是这个函数没有用绝对值。用这个函数需要注意的一点是,正负误差可以互相抵消。
- 它可以确定模型存在正偏差还是负偏差.
M B E = ∑ i = 1 n ( y i − y ^ i ) n MBE=\frac{\sum_{i=1}^{n}\left(y_{i}-\hat{y}_{i}\right)}{n} MBE=n∑i=1n(yi−y^i)
1.5 平均绝对百分比误差(Mean Absolute Pencent Error,MAPE)
MAPE = ∑ i = 1 n ∣ y i − y ^ i y i ∣ × 100 n \text { MAPE }=\sum_{i=1}^{n}\left|\frac{y_{i}-\hat{y}_{i}}{y_{i}}\right| \times \frac{100}{n} MAPE =i=1∑n∣ ∣yiyi−y^i∣ ∣×n100
相比 RMSE,MAPE 相当于把每个点的误差进行了归一化, 降低了个别离群点带来的绝对误差的影响。
1.6 Huber损失函数
L Huber ( f , y ) = { ( f − y ) 2 , ∣ f − y ∣ ⩽ δ 2 δ ∣ f − y ∣ − δ 2 , ∣ f − y ∣ > δ L_{\text {Huber }}(f, y)= \begin{cases}(f-y)^{2}, & |f-y| \leqslant \delta \\ 2 \delta|f-y|-\delta^{2}, & |f-y|>\delta\end{cases} LHuber (f,y)={(f−y)2,2δ∣f−y∣−δ2,∣f−y∣⩽δ∣f−y∣>δ
当δ~ 0时,Huber损失会趋向于MAE;当δ~ ∞(很大的数字),Huber损失会趋向于MSE。
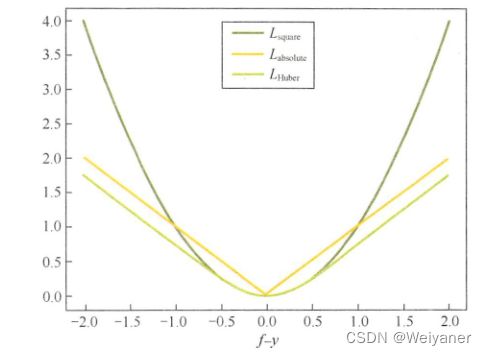
为何使用Huber损失函数?
使用MAE用于训练神经网络的一个大问题就是,它的梯度始终很大,这会导致使用梯度下降训练模型时,在结束时遗漏最小值。对于MSE,梯度会随着损失值接近其最小值逐渐减少,从而使其更准确。
在这些情况下,Huber损失函数真的会非常有帮助,因为它围绕的最小值会减小梯度。而且相比MSE,它对异常值更具鲁棒性。因此,它同时具备MSE和MAE这两种损失函数的优点。不过,Huber损失函数也存在一个问题,我们可能需要训练超参数δ,而且这个过程需要不断迭代。
当
2 Classification
2.1 0-1损失函数(zero-one loss)——Perception
指预测值和目标值不相等为1, 否则为0:
L ( Y , f ( X ) ) = { 1 , Y ≠ f ( X ) 0 , Y = f ( X ) L(Y, f(X))=\left\{\begin{array}{l}1, Y \neq f(X) \\ 0, Y=f(X)\end{array}\right. L(Y,f(X))={1,Y=f(X)0,Y=f(X)
应用:感知机模型
特点:属于非凸函数,一般来说不适用于其他的分类模型。
2.2 对数损失函数(log)——LR
L ( Y , P ( Y ∣ X ) ) = − log P ( Y ∣ X ) = − log ∏ i = 1 P ( Y = y i ∣ X = x i ) = − l o g ∏ i = 1 ∏ j = 1 p i j y i j = ∑ i = 1 N ∑ j = 1 M y i j log ( p i j ) → − 1 N ∑ i = 1 N ∑ j = 1 M y i j log ( p i j ) \begin{aligned} L(Y, P(Y \mid X))&=-\log P(Y \mid X)\\ &=-\log \prod _{i=1}P(Y=y_i|X=x_i)\\ &=-log \prod_{i=1}\prod_{j=1}p_{ij}^{y_{ij}}\\ &=\sum_{i=1}^{N} \sum_{j=1}^{M} y_{i j} \log \left(p_{i j}\right)\\ &\to -\frac{1}{N} \sum_{i=1}^{N} \sum_{j=1}^{M} y_{i j} \log \left(p_{i j}\right)\\ \end{aligned} L(Y,P(Y∣X))=−logP(Y∣X)=−logi=1∏P(Y=yi∣X=xi)=−logi=1∏j=1∏pijyij=i=1∑Nj=1∑Myijlog(pij)→−N1i=1∑Nj=1∑Myijlog(pij)
其中, Y = y 1 , . . . , y M Y={y_1,...,y_M} Y=y1,...,yM为输出变量, X = x 1 , . . . , x N X={x_1,...,x_N} X=x1,...,xN为输入变量, M为分类别数, yij是一个二值指标(取0或者1), 表示类别 j 是否是输入实例 xi 的真实类别. p i j p_{ij} pij 为模型或分类器预测输入实例 xi 属于类别 j 的概率。
应用:逻辑回归模型
对于(0-1)二分类,可以改写为如下形式:
− 1 N ∑ i = 1 N ( y i log p i + ( 1 − y i ) log ( 1 − p i ) ) -\frac{1}{N} \sum_{i=1}^{N}\left(y_{i} \log p_{i}+\left(1-y_{i}\right) \log \left(1-p_{i}\right)\right) −N1i=1∑N(yilogpi+(1−yi)log(1−pi))
特点:
- 对数损失函数能够很好的表征概率分布,适合于需要知道结果属于每类的置信度
- robust不强,对噪声敏感
2.3 指数损失函数——Adaboost
L ( Y , P ( Y ∣ X ) ) = exp [ − y f ( x ) ] L(Y, P(Y \mid X))=\exp[-yf(x)] L(Y,P(Y∣X))=exp[−yf(x)]
应用:AdaBoost算法
特点:对离群点、噪声非常敏感
2.4 Hinge损失——SVM
hinge损失函数表示如果被分类正确,损失为0,否则损失就为 1 − y f ( x ) 1-yf(x) 1−yf(x)。
L ( y , f ( x ) ) = m a x ( 0 , 1 − y f ( x ) ) L(y,f(x)) = max(0,1-yf(x)) L(y,f(x))=max(0,1−yf(x))
应用:SVM
特点
-
一般的 f ( x ) f(x) f(x) 是预测值,在-1到1之间, y y y 是目标值(-1或1)。其含义是, f ( x ) f(x) f(x) 的值在-1 和+1之间就可以了,并不鼓励 ∣ f ( x ) ∣ > 1 |f(x)|>1 ∣f(x)∣>1 ,即并不鼓励分类器过度自信,让某个正确分类的样本距离分割线超过1并不会有任何奖励,从而使分类器可以更专注于整体的误差。
-
健壮性相对较高,对异常点、噪声不敏感,但它没太好的概率解释。
2.5 交叉熵损失函数——LR
等价于对数损失函数
2.6 对数损失和极大似然函数的关系
在用sigmoid作为激活函数的时候,为什么要用交叉熵损失函数,而不用均方误差损失函数?
参考:https://zhuanlan.zhihu.com/p/58883095
