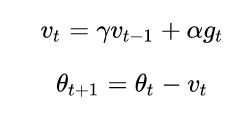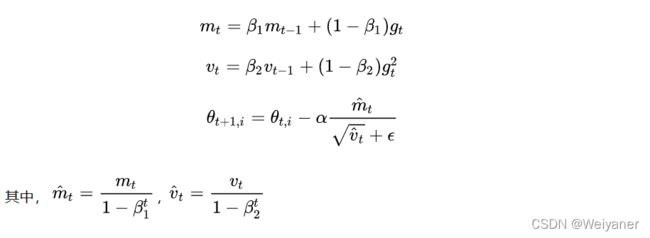机器学习/深度学习常用优化方法总结

1 随机梯度下降（SGD）

随机梯度下降在机器学习/深度学习中的重要作用不言而喻，甚至其他的许多优化方法都是根据随机梯度下降法改进而来。经典的SGD使用全局训练数据的平均损失来近似目标函数：
$$L(\theta )=\frac{1}{M}\sum _{i=1}^{M}L(f(x_i,\theta ),y_i)$$
参数求导：
$$\nabla L(\theta )=\frac{1}{M}\sum _{i=1}^M\nabla L(f(x_i,\theta ),y_i))$$
更新公式为：

$${\theta }_{i+1}={\theta }_i-\alpha \nabla L({\theta }_t)$$

由于经典的梯度下降法在每次对模型参数进行更新时，需要遍历所高的训练数据 。当 M很大时，这需要很大的计算量 ，耗费很长的计算时间 ，在实际应用中基本不可行。

因此，随机梯度下降法用单个训练数据即可对模型参数进行一次重新，大大加快了收敛速率 。 i衷方法也非常适用于数据源源不断到来的在线重新场景 。

为了降低随机梯度的方差从而使得迭代更加稳定，也为了充分利用高度优化的矩阵运算操作，在实际应用中我们会同时时处理若
干训练数据， 被称为小批量梯度下降法（ Mini-Batch Gradient Descent ）。其中m< $$L(\theta )=\frac{1}{m}\sum _{i=1}^{m}L(f(x_i,\theta ),y_i)$$
参数求导：
$$\nabla L(\theta )=\frac{1}{m}\sum _{i=1}^m\nabla L(f(x_i,\theta ),y_i))$$

关于小批量梯度下降法的问题

• 如何选取m：一般使用2次幂，可以充分利用矩阵运算操作。
• 如何挑选m个训练数据：随机排序，按顺序挑选m个。
• 如何选取学习速率：为了加快收敛速度和求解精度。采用衰减学习速率的方案：一开始较大学习率，误差曲线进入平台期后，减小学习速率。

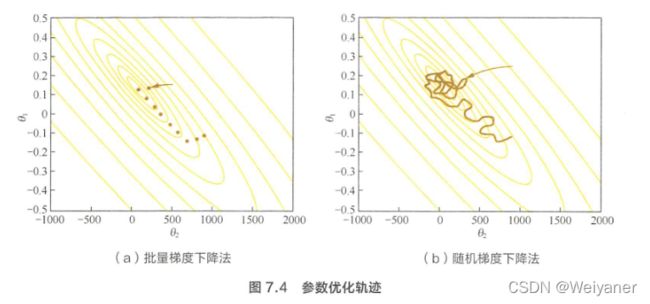
批量梯度下降法（ Batch Gradient Descent, BGD ）就
好比正常下山 ，而随机梯度下降就好比蒙着眼睛下山。
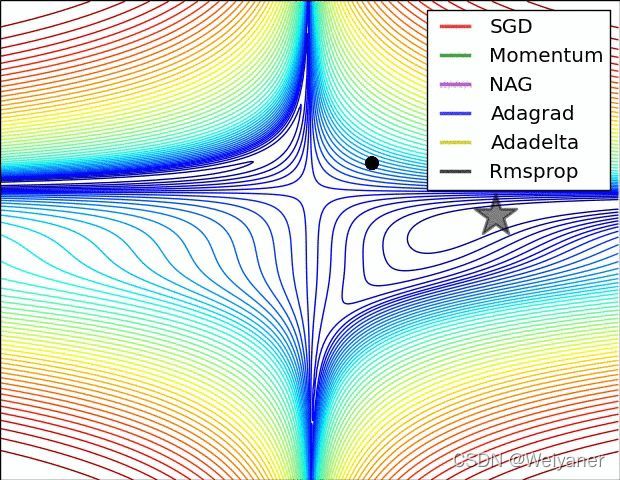
进一步地，有人会说深度学习中的优化问题本身就很难，有太多局部最优点的陷阱。这些陷阱对随机梯度下降法和批量梯度下降法都是普遍存在的 。 但对随机梯度下降法来说 ， 可怕的不是局部最优点，而是鞍点和山谷。

山谷顾名思义就是狭长的山间小道，左右两边是峭壁；鞍点的形状像是一个马鞍 ， 一个方向上两头翘，另 一个方向上两头垂 ， 而中心区域是一片近乎水平的平地 。 为什么随机梯度下降法最害怕遇上这两类地形呢？在山谷中，准确的梯度方向是沿山道向下，稍有偏离就会撞向山壁，而粗糙的梯度估计使得它在两山壁间来回反弹震荡，不能沿 山道方向迅速下降 ，导致收敛不稳定和收敛速度慢。在鞍点处 2 随机楠度下降法会走入一片平坦之地（此时离最低点还很远，故也称 plateau ） 。 想象一下蒙着双眼只凭借脚底感觉坡度 1 如果坡度很明显，那么基本能估计出下山的大致方向， 如果坡度不明显 3 则很可能走锚方向 。 同样，在梯度近乎为零的区域，随机梯度下降法无法准确察觉出梯度的微小变化，结果就停滞下来。

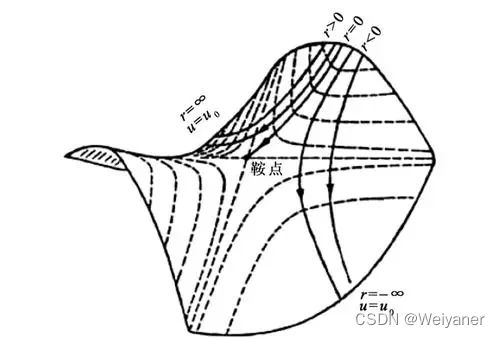
为了克服鞍点和山谷的影响，对随机梯度下降提出了以下改进算法

2 基于动量（Momentum）的SGD

动量是模拟物理中动量的概念，迭代点的更新方向由当前的负梯度方向和上一次的迭代更新方向加权组合形成。

• 一方面是加快下降，因为在下降的方向上不断累积动量，使得下降的速度变快了。
• 另一方面，这样的方式可以使迭代跳出鞍点和部分较浅的局部极小值点，使更有可能找到全局极小值。
  

3 AdaGrad

上面的动量是基于历史信息的，AdaGrad是基于环境感知的。针对不同参数的经验性判断，自适应的确定学习速率。不同参数的更新速率不同，更新频率越快步子越小。

4 Adam

考虑了动量和环境感知。

优点：

• 结合了AdaGrad善于处理稀疏数据的能力
• 善于处理非平滑目标
• 对内存需求小
• 具备自适应能力
• 可用于大多数非凸优化——适用于大数据集和高维空间

5 关于优化方法的选择

1. 对于稀疏数据，尽量选择自适应能力的优化方法，不用手动调节
2. SGD训练时间更长，但是只要初始化和学习率调节好，效果更可靠
3. 如果对于深层网络，可以使用学习率自适应的优化方法，更快收敛