浅谈WQS二分、带权二分、凸优化与一类斜率优化DP
幕天
- 题意
- 一个简单的转化
- 二维DP
-
- 朴素
- 斜率优化
- 带权二分
-
- 我们先看一道简单题
-
- 题意
- 分析
- 代码
- 进入正题
-
- 题目回顾
- 分析
-
- 加权
- 权与段数的关系
-
- 单调性
- 两个问题
- DP
-
- 朴素DP
- 斜率优化
-
- 就题论题的分析方法
- 一个普适的结论
- 代码
- 后记
除最后一张普适公式外,文中所有图像和公式均为原创,转载请附出处谢谢!!!
题意
[BZOJ 4518] Sdoi2016 征途
求 n n n个数 a 1 , a 2 , ⋯ , a n a_1,a_2,\cdots,a_n a1,a2,⋯,an分成 m m m段,求每段的数之和的方差 s 2 s^2 s2的最小值,输出 s 2 × m 2 s^2\times m^2 s2×m2。
( 1 ≤ n ≤ 2 × 1 0 5 1\leq n\leq2\times10^5 1≤n≤2×105, 1 ≤ m ≤ n 1\leq m\leq n 1≤m≤n, ∑ i = 1 n a i ≤ 3 × 1 0 4 \sum\limits_{i=1}^{n}a_i\leq3\times10^4 i=1∑nai≤3×104,实际上数据可以开成这样)
一个简单的转化
设第 i i i段数之和是 p i p_i pi,众所周知方差 s 2 = ∑ i = 1 m ( p i − p ‾ ) 2 m s^2=\dfrac{\sum\limits_{i=1}^{m}(p_i-\overline{p})^2}{m} s2=mi=1∑m(pi−p)2,其中 p ‾ = ∑ i = 1 m p i m = ∑ i = 1 n a i m \overline{p}=\dfrac{\sum\limits_{i=1}^{m}p_i}{m}=\dfrac{\sum\limits_{i=1}^{n}a_i}{m} p=mi=1∑mpi=mi=1∑nai。
所以 s 2 × m 2 = m ( ∑ i = 1 m ( p i − p ‾ ) 2 ) = m ( ∑ i = 1 m p i 2 − 2 × p ‾ × ∑ i = 1 m p i + m × p ‾ 2 ) = m ∑ i = 1 m p i 2 − 2 × ( ∑ i = 1 n a i ) 2 + ( ∑ i = 1 n a i ) 2 = m ∑ i = 1 m p i 2 − ( ∑ i = 1 n a i ) 2 \begin{aligned} s^2\times m^2&=m\left(\sum\limits_{i=1}^{m}(p_i-\overline{p})^2\right)\\ &=m\left(\sum\limits_{i=1}^{m}{p_i}^2-2\times\overline{p}\times\sum\limits_{i=1}^{m}p_i+m\times\overline{p}^2\right)\\ &=m\sum\limits_{i=1}^{m}{p_i}^2-2\times\left(\sum\limits_{i=1}^{n}a_i\right)^2+\left(\sum\limits_{i=1}^{n}a_i\right)^2\\ &=m\sum\limits_{i=1}^{m}{p_i}^2-\left(\sum\limits_{i=1}^{n}a_i\right)^2 \end{aligned} s2×m2=m(i=1∑m(pi−p)2)=m(i=1∑mpi2−2×p×i=1∑mpi+m×p2)=mi=1∑mpi2−2×(i=1∑nai)2+(i=1∑nai)2=mi=1∑mpi2−(i=1∑nai)2
发现 ( ∑ i = 1 n a i ) 2 \left(\sum\limits_{i=1}^{n}a_i\right)^2 (i=1∑nai)2是定值,所以要求的就是 m ∑ i = 1 m p i 2 m\sum\limits_{i=1}^{m}{p_i}^2 mi=1∑mpi2的最小值。
二维DP
(不考虑时空问题)
m m m也是定值,所以只需要求 ∑ i = 1 m p i 2 \sum\limits_{i=1}^{m}{p_i}^2 i=1∑mpi2的最小值。
朴素
先处理前缀和 S i S_i Si,一个直观的思路是 d p [ i ] [ j ] dp[i][j] dp[i][j]表示前 i i i个数,分成 j j j段,的平方和的最小值。那么这个 O ( n 3 ) O(n^3) O(n3)的DP就超级简单: d p [ i ] [ j ] = min { d p [ k ] [ j − 1 ] + ( S i − S k ) 2 } dp[i][j]=\min\{dp[k][j-1]+(S_i-S_k)^2\} dp[i][j]=min{dp[k][j−1]+(Si−Sk)2}
斜率优化
机智的人会发现这个是个斜率优化的板子(我们等会进行理解)可以优化到 O ( n 2 ) O(n^2) O(n2),虽然可以再滚动一维数组,但是时间还是过不了。
带权二分
众所周知,带权二分,又叫wqs二分,凸优化等。它的应用范围很脑残:一般是让你在一堆元素当中恰好选 x x x个/分 x x x段,以达成某个条件。
我们先看一道简单题
题意
[BZOJ 2654] tree
给你一个无向带权连通图,每条边是黑色或白色。让你求一棵最小权的恰好有 need \text{need} need条白色边的生成树。
分析
可能你会考虑到用破圈法换边,但是这个的正确性是fake的。或许你能骗到几十分。下面是这个方法的解释:
先用黑边做一个最小生成树,然后从小到大依次加入白边,每加入一条就用破圈法找到这个圈里面最大权的黑边,替换。
反例:(红色的是白边), need = 1 \text{need}=1 need=1
我们给每个白边的权加 w w w( w w w可以是负数),再直接做最小生成树,可以得到一个白边的数量 x x x,很显然 w w w跟 x x x成反相关,也就是说: w w w越大,选的白边越少。
于是二分 w w w即可。
这就是最基本的带权二分。
对了这道题可以先把黑边和白边分别排序,check的时候用Kruskal归并排序,时间复杂度少一个 log n \log n logn。
代码
我没有写归并,而且很丑。
#include进入正题
题目回顾
我们通过一个简单的转化,将原问题变成了求 m ∑ i = 1 m p i 2 m\sum\limits_{i=1}^{m}{p_i}^2 mi=1∑mpi2的最小值。
分析
同样的我们想办法给某个东西加一个权。
加权
好了,就是给每段的平方( p i 2 {p_i}^2 pi2)加一个权 c c c。
像上一道题一样,这个时候的段数已经不重要了。所以我们求的是,分的段数没有限制的情况下(我们现在令这个段数为 x x x) ∑ i = 1 x ( p i 2 + c ) \sum\limits_{i=1}^{x}\left({p_i}^2+c\right) i=1∑x(pi2+c)的最小值,如果在这个最小值的状态下 x x x恰好等于 m m m,原问题就解决了(时刻记住,取得最小值是先决条件)。
权与段数的关系
单调性
然后我们来感性理解一下这个段数 x x x和权值 c c c的关系,以确定能否二分,令:
f ( x ) = min { ∑ i = 1 x p i 2 } g ( c ) = min { ∑ i = 1 x ( p i 2 + c ) } = min { f ( x ) + x ⋅ c } \begin{aligned} f(x)&=\min\{\sum\limits_{i=1}^{x}{p_i}^2\}\\ g(c)&=\min\{\sum\limits_{i=1}^{x}\left({p_i}^2+c\right)\}=\min\{f(x)+x\cdot c\} \end{aligned} f(x)g(c)=min{i=1∑xpi2}=min{i=1∑x(pi2+c)}=min{f(x)+x⋅c}
容易发现的是, f ( x ) f(x) f(x)单减(分的段数越多,代价越小):

随便找个 x 0 x_0 x0:

那么 f ( x 0 ) + x 0 ⋅ c f(x_0)+x_0\cdot c f(x0)+x0⋅c长这样( tan θ = c \tan\theta=c tanθ=c):
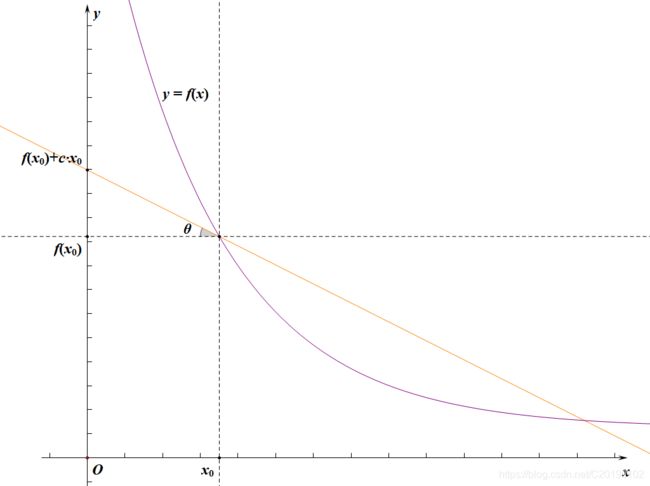
g ( c ) g(c) g(c)显然就是斜率为 − c -c −c的直线(下图中的红线)与 f ( x ) f(x) f(x)的切线的截距:
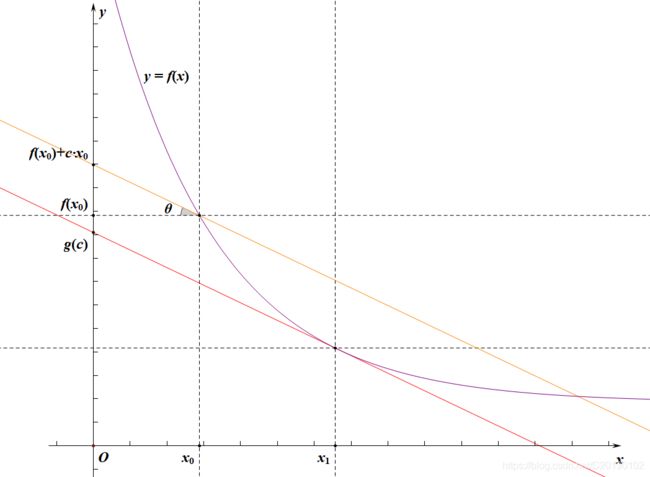
所以我们的忘情水二分实际上是二分的斜率,求切点的横坐标,使切点的横坐标逼近 m m m!
你可能会问,为什么不直接求 f ( m ) f(m) f(m),要是能求就不需要忘情水了啊!(其实可以求,就是最开始的那个二维DP+斜率优化,只是会超时)。
或者说,忘情水直接灭掉了DP的“cnt”那一维!
其实上面那些没什么用,你只需要很明显地发现由于 f ( x ) f(x) f(x)单减, g ( x ) g(x) g(x)和 c c c正相关即可: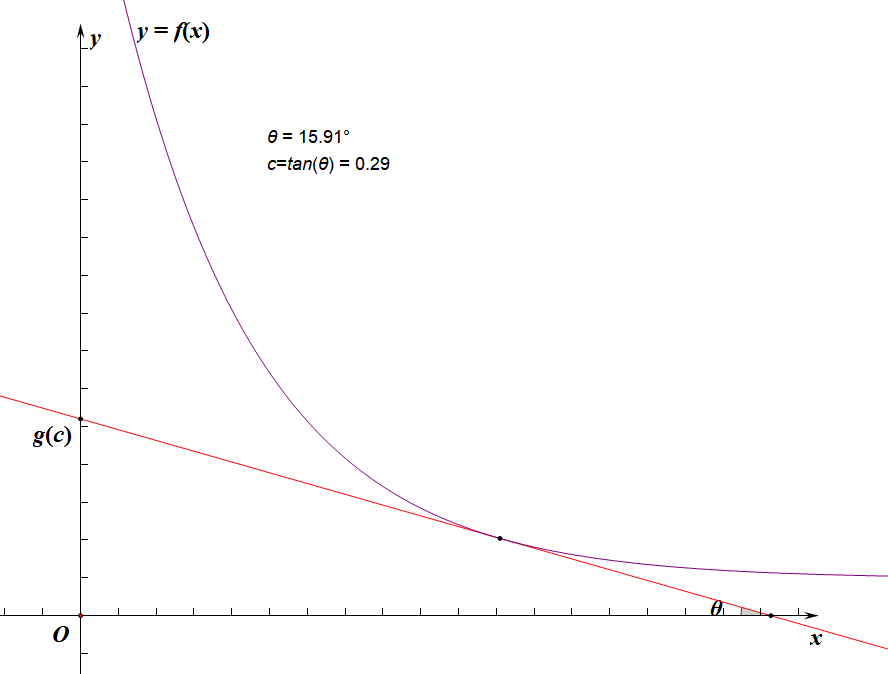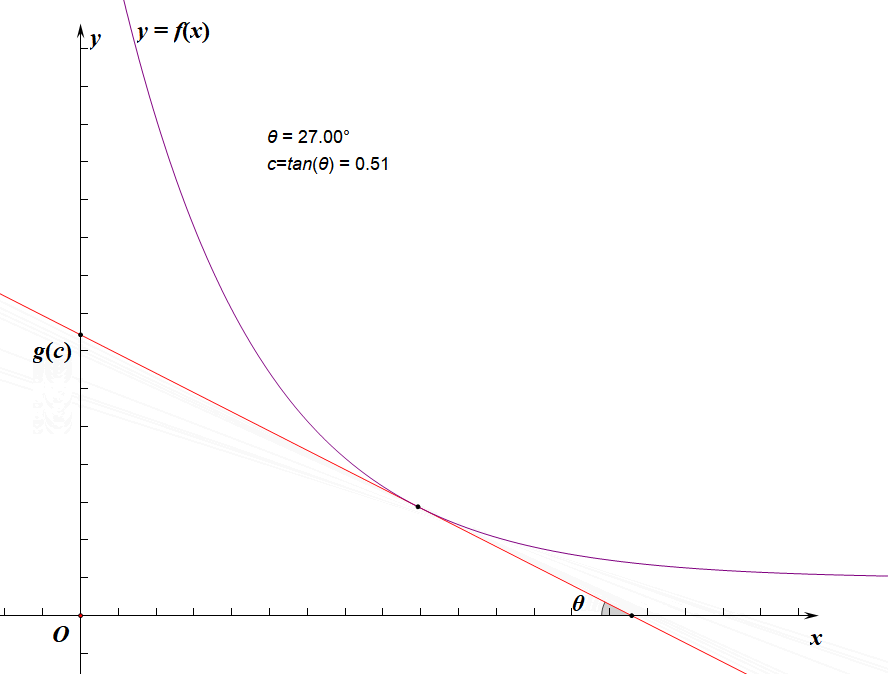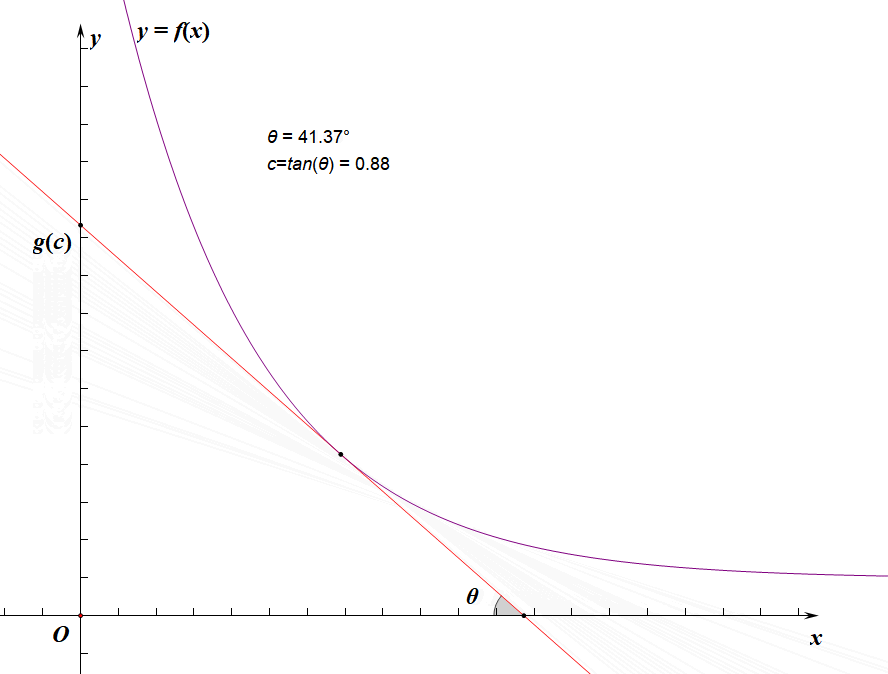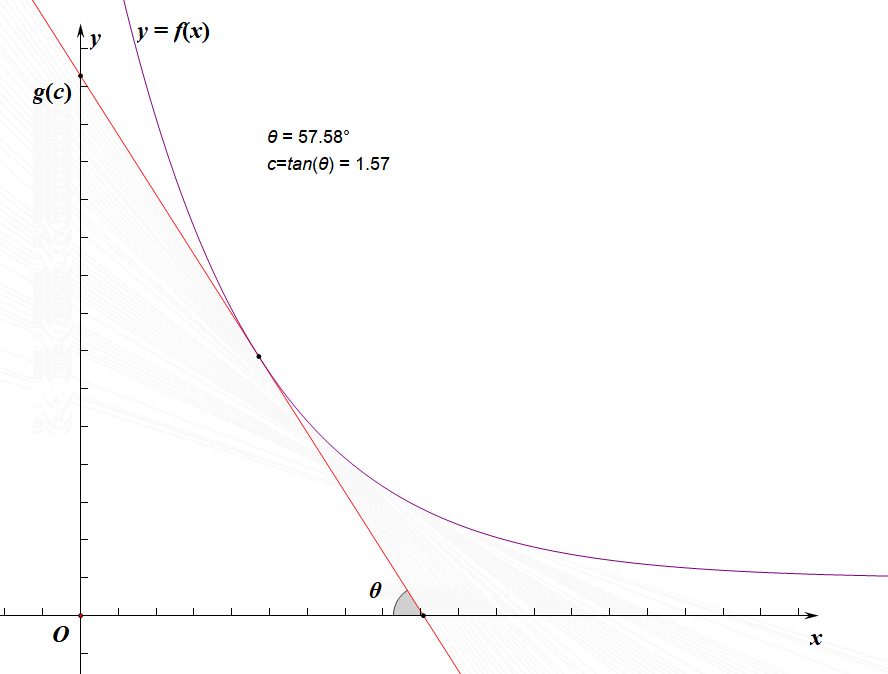
两个问题
那么,在 c c c为整数的范围内,到底能不能二分出一个 x x x恰好等于 m m m呢?
这个时候就不能考虑连续函数了,因为 f ( x ) f(x) f(x)(它本身就)是离散的(所以上面这些图都不严谨):
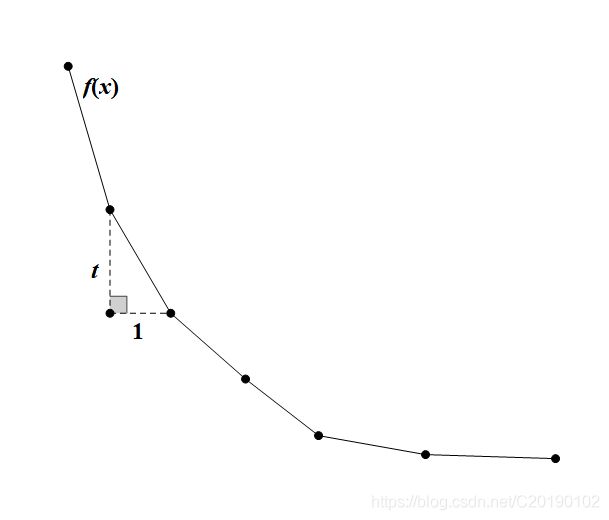
注意到 f ( x ) f(x) f(x)的定义域和值域都是 Z \Z Z,相邻点的横坐标之差都是 1 1 1,这说明了, f ( x ) f(x) f(x)的任意一条切线的斜率(上图中的 t t t)肯定是整数!于是我们一定可以二分到一个整数斜率!
但是还有一个问题:
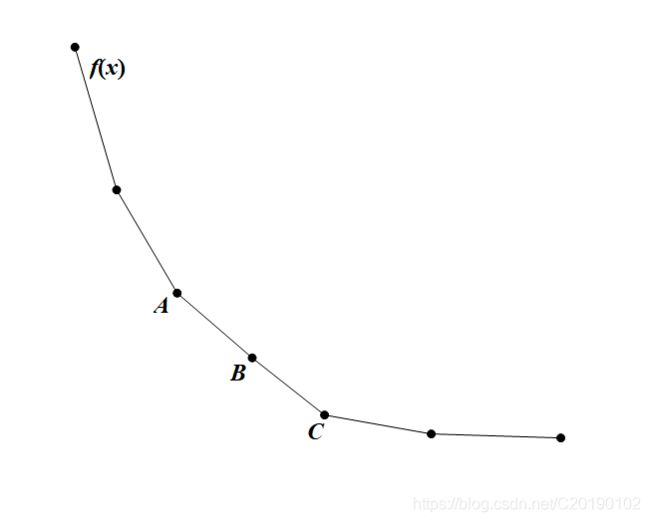
图中 A , B , C A,B,C A,B,C三点共线,当你二分到 k l A C k_{l_{AC}} klAC时,到底哪个横坐标算最终的 x x x?事实上,三个都可以,也就是说 x A , x b x_A,x_b xA,xb或 x c = m x_c=m xc=m,这个斜率都是对的!但这个返回什么其实不影响,因为你不输出方案,二分最终的 L e f t Left Left和 R i g h t Right Right最后肯定在 A C AC AC以内,但不一定是 m m m(因写法而不同), A , B , C A,B,C A,B,C三个点对应的答案肯定是对的(答案仅与 g ( c ) g(c) g(c)和最开始那个简单的转换里面的常数有关,而 A , B , C A,B,C A,B,C三点 g ( c ) g(c) g(c)都一样),但是输出方案就会有问题,因为(就这道题来说) x A ≠ x C ≠ x C x_A\neq x_C\neq x_C xA=xC=xC(还记得 x x x实际意义是什么吗,分成的段数!)。
上面这段话只是在解释这个算法的正确性,如果不能看懂也无妨,毕竟是细节问题,当然欢迎提问。
DP
朴素DP
熟练地写出求 ∑ i = 1 x ( p i 2 + c ) \sum\limits_{i=1}^{x}\left({p_i}^2+c\right) i=1∑x(pi2+c)最小值的DP式子( S i S_i Si还是前缀和) d p [ i ] = min { d p [ j ] + ( S i − S j ) 2 + c } dp[i]=\min\{dp[j]+(S_i-S_j)^2+c\} dp[i]=min{dp[j]+(Si−Sj)2+c}这个显然是 O ( n 2 ) O(n^2) O(n2),总的复杂度是 O ( n 2 log S n ) O(n^2\log S_n) O(n2logSn),以原题的数据范围是过得了的。
斜率优化
就题论题的分析方法
鉴于我还没有讲过斜率优化,这里将会详细讲解一下,从入门开始。
假设对于某个 d p [ i ] dp[i] dp[i],有从 j 1 j_1 j1转移比从 j 2 j_2 j2转移过来更优,那么: d p [ j 1 ] + ( S i − S j 1 ) 2 + c < d p [ j 2 ] + ( S i − S j 2 ) 2 + c dp[j_1]+(S_i-S_{j_1})^2+c
这个很像斜率式对吧,所以对于一个 j j j,我们把它做成一个点 P j ( S j , d p [ j ] + S j 2 ) P_j\left(S_j,dp[j]+{S_j}^2\right) Pj(Sj,dp[j]+Sj2),左边就是直线 P j 1 P j 2 P_{j_1}P_{j_2} Pj1Pj2的斜率,再做一条斜率为 2 S i 2S_i 2Si的直线 l l l,它们就是这个样子的( k P j 1 P j 2 > k l k_{P_{j_1}P_{j_2}}>k_l kPj1Pj2>kl, S j 1 < S j 2 S_{j_1}

显然 S j S_j Sj是单调增的,那么,由于DP是从小到大枚举下标的,那么我们用当前这个 d p [ i ] dp[i] dp[i]维护这个“凸包”(为什么叫这个名字你一会就知道了)时, P i P_i Pi也是从左到右加进去的(这就是为什么要讨论 S j 1 < S j 2 S_{j_1}
- 情况一
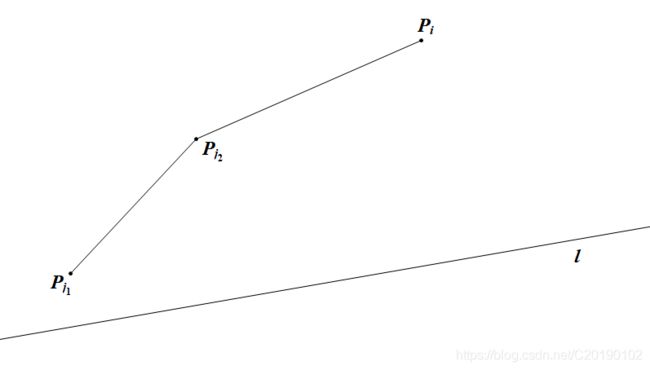 由于 2 S i 2S_i 2Si也是单调,那么 l l l接下来会逆时针转成这样:
由于 2 S i 2S_i 2Si也是单调,那么 l l l接下来会逆时针转成这样:

或这样:

比较这三种情况中三条线的斜率,可以得到 j 2 j_2 j2完全没有用,所以我们删掉 j 2 j_2 j2,变成这样:
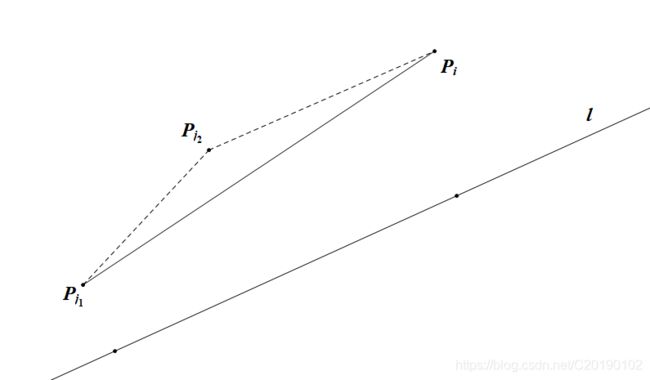
- 情况二

由于 2 S i 2S_i 2Si也是单调,那么 l l l接下来会逆时针转成这样:
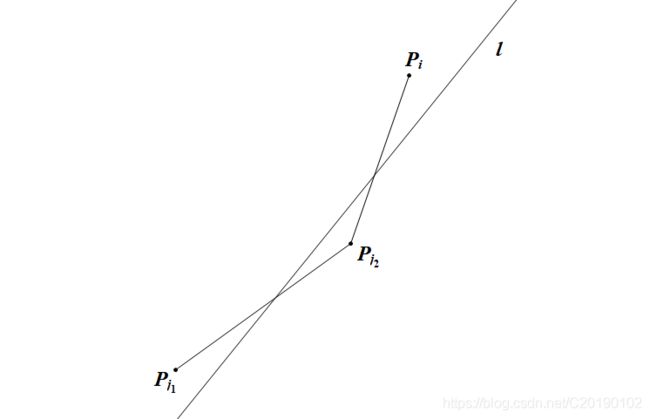
同情况一,还有这样:
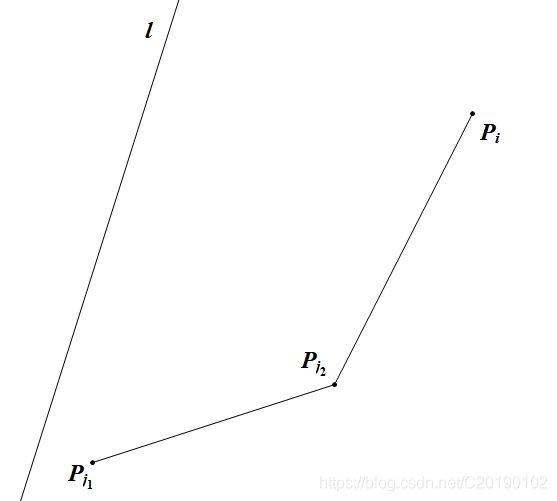
比较这些情况中三条线的斜率,可以得到 j 2 j_2 j2是有用的,所以要保留 j 2 j_2 j2。
于是,想象一下,很多的 j j j到了一起,变成了这样:
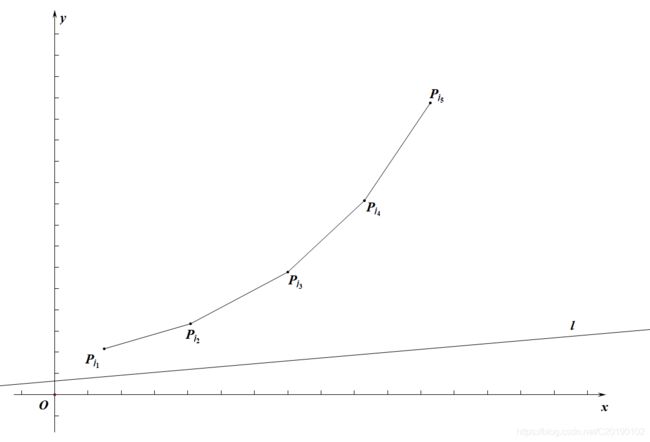
我们形象地把它称为下凸包。
梳理一下,我们现在有一个这样的下凸包,要得到 d p [ i ] dp[i] dp[i]。
由于 i i i往后移了一位,所以 2 S i 2S_i 2Si会变大, l l l会逆时针转一点,就可能导致凸包开头的某些斜率太小的线段不合法,例如下图中红色的 P j 1 , P j 2 P_{j_1},P_{j_2} Pj1,Pj2就该被删掉(红色线段斜率比 l l l小了),因为从这时开始,随着 l l l不断逆时针转,它们一辈子都不能比 P j 3 P_{j_3} Pj3更优了:

处理掉不合法的点过后,再看剩下的点,比较一下斜率可得 P j 3 P_{j_3} Pj3优于 P j 4 P_{j_4} Pj4优于 P j 5 P_{j_5} Pj5(实际上很明显的是越靠左越优,因为斜率是递增的,并且都比 k l k_l kl大)。
所以, d p [ i ] dp[i] dp[i]直接从 d p [ j 3 ] dp[j_3] dp[j3]转移来即可。
然后,将 i i i按照上面的维护下凸包的方法加入到最后(右端)即可。
一个普适的结论
Tip: T ( j 1 , j 2 ) T(j_1,j_2) T(j1,j2)是下面这个式子里左边那坨, g ( i ) g(i) g(i)就是右边那坨。
( d p [ j 1 ] + S j 1 2 ) − ( d p [ j 2 ] + S j 2 2 ) S j 1 − S j 2 > 2 S i \dfrac{(dp[j_1]+{S_{j_1}}^2)-(dp[j_2]+{S_{j_2}}^2)}{S_{j_1}-S_{j_2}}>2S_i Sj1−Sj2(dp[j1]+Sj12)−(dp[j2]+Sj22)>2Si

(来自课件,侵删)(其实这个没有什么用,现推还能保证准确性)
代码
更多细节一定要看代码,虽然比较丑(#define int long long是被逼迫的!)
#include后记
这篇文章是我呕心沥血制作,经超级大神犇cxh的细心指导后(他真的很强!!!)完成(这个是他关于这个问题的博客,他最后关于二分细节的探讨我没有写,可以参考!)。有问题一定要提出!!!
