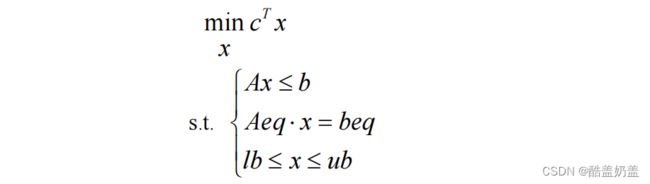数学建模基础笔记——线性规划模型

(1)标准形式

---

x_i-决策变量
z-目标函数
c-价值向量
b-资源向量

(2)三要素

---

决策变量
目标函数
约束条件

(3)解的理解

---

（1）可行解:满足条件
（2）最优解，是目标函数达到最大值或最小值的解
（3）可行域

(4)灵敏度分析

---

（1）参数变化时，最优解会发生什么变化
（2）若保持最优解，参数需在什么范围内变化

(5)基于求解器的求解方法

---

函数调用格式

[x,fval] = linprog(c,A,b)
[x,fval] = linprog(c,A,b,Aeq,beq)
[x,fval] = linprog(c,A,b,Aeq,beq,lb,ub)

注意：三种不同的写法，有哪个参数就写哪个
在命令行窗口输入
示例
：

c=[4,3];b=[10,8,7];
a=[2,1;1,1;0,1];lb=zeros(2,1);
[x,fval]=linprog(c,-a,-b,[],[],lb)
y=-fval

(6)基于问题求解的求解方法

接上题

prob=optimproblem('ObjectiveSense','max')%目标函数最大优化问题
 c=[4;3];b=[10;8;7];
a=[2,1;1,1;0,1];
x=optimvar('x',2,'LowerBound',0);
prob.Objective=c'*x
prob.Constraints.con=a*x<=b;
[sol,fval,flag,out]=solve(prob)
sol.x

其中prob=optimproblem(‘ObjectiveSense’,‘max’)为求解最大值，prob=optimproblem为最小值