[论]【MGT】Meta Graph Transformer: A Novel Framework for Spatial–Temporal Traffic Prediction

Meta Graph Transformer: A Novel Framework for Spatial–Temporal Traffic Prediction

原文，见这里
作者：Xue Ye , Shen Fang , Fang Sun ， Chunxia Zhang , Shiming Xian
期刊：爱思唯尔Neurocomputing
关键字：交通预测，时空建模，元学习，注意机制，深度学习
相关博文：翻译
代码：https://github.com/lonicera-yx/MGT
或 gitee code

---

bib

@article{2021Meta,
  title={Meta Graph Transformer: A Novel Framework for Spatial–Temporal Traffic Prediction - ScienceDirect},
  author={ Xue, Yab  and  Shen, Fab  and  Fang, S. C.  and  Cz, D  and  Sxa, B },
  journal={Neurocomputing},
  volume={491},
  pages={544-563},
  year={2021},
}

知识点参考

1. Laplacian Eigenmaps：《四大机器学习降维算法》， 《推导方法》，《不完整的csdn》

摘要

准确的交通预测是提高智能交通系统性能的关键。这项任务的关键挑战是如何在尊重和利用数据的空间和时间异质性的同时，正确地建模复杂的交通动态。本文提出了一种名为元图转换器(Meta Graph Transformer, MGT)的新框架来解决这个问题。MGT 框架是对原始转换器的推广，该转换器用于对自然语言处理中的向量序列进行建模。具体来说，MGT有一个编码器-解码器架构。编码器负责将历史交通数据编码为中间表示，而解码器自回归预测未来的交通状态。MGT的主要构建模块是三种类型的注意层，分别是时间自我注意(TSA)、空间自我注意(SSA)和时间编码器-解码器注意(TEDA)。它们都是多头结构。编码器和解码器都使用TSA和SSA来捕获时间和空间相关性。解码器采用TEDAs，使解码器中的每个位置都能在时间上参与输入序列中的所有位置。通过利用多个图，SSA可以利用各种诱导偏差进行稀疏空间注意。为了便于模型对时间和空间条件的感知，从外部属性学习时空嵌入(spatial - temporal Embeddings, sts)，这些外部属性由时间属性(如顺序、一天中的时间)和空间属性(如拉普拉斯特征映射)组成。这些嵌入通过元学习被所有的注意层利用，从而赋予这些层空间-时间异质性感知(STHA)的属性。在三个真实交通数据集上的实验证明了我们的模型比几种最先进的方法的优越性。

1. Introduction

交通基础设施的发展和人们出行需求的不断变化，呼唤交通资源的有效优化和高效配置。解决这些问题的需要就投在了智能交通系统(ITS)领域。ITS的核心是两大支柱**:智能交通基础设施和数据分析算法**。前者可以从各种设备（如环路检测器和地铁票价采集系统）收集大量交通数据，而后者在将交通数据转换为有用信息方面起着关键作用。交通量预测是智能交通系统（ITS）的基本任务之一。流量预测的目标是根据网络中所有位置的历史记录(即前$P$个时间步的流量状态)，预测网络中所有位置未来的流量状态(即下一个$H$时间步的流量状态)。图1给出了时空交通预测的简要说明。准确的交通预测可以指导交通部门更好地管理和规划。然而，复杂的空间和时间相关性使这项任务具有挑战性。

Fig.1 时空交通预测的插图。

在早期，统计模型在解决交通预测问题中很流行，比如自回归综合移动平均方法[1,2]、卡尔曼滤波[3]、向量自回归模型[4]。这些模型被严格的数学理论验证.然而，它们的性能往往受到可能不正确的交通数据假设（线性、平稳性等）的限制。

随后，各种基于机器学习的流量预测方法被开发出来，如支持向量回归[5]、随机森林[6]、k最近邻模型[7]等。这些方法有能力建模非线性相关性和提取更复杂的相关性，特别是当大规模数据可用时。然而，这些模型的有效性很大程度上取决于复杂的特征工程，这可能是困难和耗时的。

近十年来，深度学习方法在图像识别[8,9]、目标检测[10,11]、机器翻译[12,13]等各个领域都带来了突破。深度学习的强大能力也吸引了交通领域的研究人员。将区域划分为网格，利用二维或三维(含时间维度)卷积进行交通预测[14-18]。但是，这种基于网格的方法没有考虑交通数据的底层图结构。另一个研究方向是时空图神经网络(spatial - temporal Graph Neural Networks, STGNNs)[19]，其空间信息的交换是由图来引导的。这种方法最近很流行。典型的模型有STGCN[20]和DCRNN[21]。

顾名思义，STGNN框架通常涉及建模的两个方面:一个沿空间维度，另一个沿时间维度。这两个方面的建模可以分别进行[20,22-26]，也可以同时进行[21,27 - 30]。后者的一种常见做法是将递归神经网络(RNN)中的矩阵乘法替换为图卷积。STGNN框架的主要挑战是有效捕获交通网络演化过程中复杂的时空相关性，从而尽可能提高预测的准确性。

在空间建模方面，许多工作都是在静态图[21,20]的基础上进行图卷积[31,32]。该图通常由真实的交通网络构建，其边权值从距离上反映了两个节点的接近程度。虽然基于距离的图在一定程度上揭示了地理位置接近的地点之间的相互影响，但它在远程建模[33]中是不足的。为了弥补这一缺陷，Graph WaveNet[22]和AGCRN[30]提出通过节点嵌入学习隐藏的空间依赖，而PVCGN[27]和Multi-STGCnet[23]从不同角度构建多个图进行空间特征学习。这些方法的问题是，在每个图(预先构建或学习)中，分配给相邻节点的权值在训练后是固定的。这种方法不适用于空间相关性会随时间变化的交通任务。因此，有研究者考虑利用注意力机制[12]来动态确定邻居的权重[34,28,24-26]。 通常，分配给邻居的注意系数是通过参数化函数计算的，中心节点的特征和相邻节点的特征作为输入输入输入到该函数中。这样，就可以用动态权重代替静态权重进行特征聚合，从而大大增强了模型的适应性。

然而，大多数基于注意力的方法都有一个显著的缺陷:参数在所有位置和时间间隔中是共享的，因此节点之间的相关性仅取决于它们各自的特征。为什么这很重要?假设有一对地铁站(图2):A站位于商业中心，B站位于居民区。高峰时段的交通以通勤为主，A站的出流量与b站的入流量高度相关，而高峰时段以外的交通随机性较大，导致A站与b站的相关性较弱。$(a,b)$和$(c,d)$分别为7:00和14:00。前者是在高峰时间，而后者不是。交通数据在a和c处的值相同，同理b和d处的值也相同。如果相关性仅依赖于特征，那么a和c相关，b和d相关，然而事实并非如此。这表明空间相关性本质上是时间异质性的。此外，空间相关性还需要考虑空间异质性，典型交通网络中的不同节点甚至不具有相同的局部拓扑。因此，考虑到时空异质性似乎是空间建模的一个自然的改进方向。

Fig.2 时空异质性图解。A和B是两个地铁站。

在时间建模方面，现有的方法主要分为三类:基于RNN的方法[21,23,28,27,30]、基于cnns的方法[20,22,25]和基于注意力的方法[34,24,26]。rnn[35,13]最早被提出用于自然语言处理，试图同时记忆长、短期信息。然而，由于[36]的梯度消失问题，RNN很难捕获长期依赖[37]。此外，rnn的顺序性使得其在训练时不可能被并行化。同时，基于CNNs的方法通过在时间维度上使用一维卷积[38]实现并行化。然而，受限于内核大小，一维卷积无法捕获长期依赖关系。尽管当足够多的一维卷积层堆叠在[39]时，任何时间点对最终都会被关联起来，但这种关联会被稀释，无法有效利用。相比之下，基于注意力的方法通过关注每个时间位置来有效地学习长期依赖，并且可以很容易地并行化。

就像空间建模一样，时空异质性可以被用来提高时间建模的性能。考虑图2中对$(e,b)$和$(f,d)$，分别具有相同的时间跨度(1小时)和相同的值。因为$(e,b)$取自高峰时段，它们的相关性应该强于$(f,d)$。这种差异将被时空同质的方法所忽略。

沿着这条路线，一些作品[29,24,30,26]考虑了时空异质性。但他们要么在序列层次上考虑异质性[29,30,26]，要么通过时空嵌入和输入（特征）的直接串联[24]或求和[29,26]引入异质性。前者无法合并全局时间信息，而后者混淆了两种不同类型数据之间的关系。

本文提出了一个元图转换器(Meta Graph Transformer, MGT)框架来解决流量预测问题。管理行为在时间和空间维度上充分利用了注意机制。因此，它享有所有关注的好处，如动态关联、高效的长期建模和容易并行。此外，我们设计了一个元学习过程（因此被称为元图转换器），将从外部时间和空间属性中学习到的元知识整合到注意层中，从而使我们的模型能够执行时空异质性感知（STHA）注意。此外，我们的空间注意层集成了多个图，从而考虑了各种类型的空间相关性。我们的模型的贡献总结如下:

• 本研究开发了一个框架，将元学习整合到注意机制中，以捕捉交通预测任务中的时空异质性。
• 将外部的空间和时间属性融合到空间-时间嵌入(spatial - temporal Embeddings, STEs)中，在此指导下设计了三种类型的注意层，在时间和空间维度上执行 STHA 操作.
• 创建了一个多图版本的空间注意，以更好地捕捉不同类型的空间依赖关系。
• 在三个交通数据集上进行了大量实验，以评估我们提出的模型。结果表明，我们的模型明显优于最先进的方法。

2. Related Work

2.1. Spatial–Temporal Traffic Prediction

交通预测是ITS[40]中的经典任务，近年来已经取得了很大的进展[41-55]。早期的工作主要集中在统计方法 上，如自回归综合移动平均方法[1,2]、卡尔曼滤波[3]、向量自回归模型[4]等。虽然这些模型有复杂的数学理论支持，但不切实际的假设，如线性和平稳性，限制了它们在交通预测中的表现。基于机器学习的支持向量回归[5]、随机森林[6]和k-最近邻模型[7]等方法克服了这些局限性。这些模型能够对更复杂的依赖关系进行建模，并受益于大规模数据。但是手工进行特征工程的需要使它们成为劳动密集型和耗时的。

深度学习 [56]通过自动提取网络中的表示，绕过了复杂的特征手工制作过程。受卷积神经网络(Convolutional Neural Networks, CNNs)在图像任务上的巨大成功[8-11]的启发，交通社区的研究人员将感兴趣区域划分为2D或3D细胞[14-18]，并将其视为具有卷积的图像。例如ST-ResNet[14]利用基于cnn的残差神经网络来预测全市的人群流动。STDN [17]通过本地CNN和LSTM预测区域交通状态。ST-3DNet[18]引入3D卷积，自动捕获交通数据在空间和时间维度上的相关性。

由于交通网络自然是图结构 的，许多研究人员考虑直接在图上建模交通数据。这些模型统称为STGNNs [19]。沿空间和时间维度的建模可以分别进行[20,22-26]或同时进行[21,27-30]。对于后者，一种常见的做法是用图卷积代替RNN网络中的矩阵乘法[21,27,28,30]，另一种方法是直接在局部时空图[29]上进行卷积。

在空间建模方面，许多文献[21,20]采用了静态图上的局部图卷积[31,32]，该静态图是由真实交通网络构建的。然而，由于其他交通关系，空间依赖可能是非本地的，如出发地-目的地相关性和功能相似性。为了解决这个问题，

Graph WaveNet[22]和AGCRN[30]都通过节点嵌入学习了一个隐藏的空间依赖。
PVCGN[27]构造一个物理图和两个基于领域知识的虚拟图来进行图卷积。
Multi-STGCnet[23]设计了三个空间矩阵来提取目标站的空间相关性，将目标站的空间相关性分为近邻居、中邻居和远邻居。

上述方法的共同点是，在测试阶段，每个图上的边权值都是固定的。但实际上，节点之间的空间关系可能会随着时间的推移而改变。为了进一步提高空间建模的适应性，许多研究利用关注机制[12]根据输入动态分配边缘权值。

ASTGCN【34】使用空间注意机制【57】捕捉动态空间相关性。
MRA-BGCN[28]利用多范围注意机制，有效地利用多个范围信息，生成集成表示。
LSGCN[25]提出了一种基于门控机制的图关注网络cosat，用于捕获空间信息。
GMAN[24]和ASTGNN[26]采用scale - dot - product attention机制对空间相关性进行建模。

关于时间建模，现有的方法主要分为三类:基于RNN的方法、基于CNNs的方法和基于注意力的方法。
基于rnn的方法[21,23,28,27,30]通常利用长短期记忆 (LSTM)[35]或门控循环单元(GRU)[13]作为时间建模的基本块。一些研究[21,28,27,30]通过特定的空间卷积来修改RNN中的矩阵乘法，以同时捕获空间和时间相关性。虽然rnn被提出用于建模长序列，但由于梯度消失问题[36]，它们在捕获长期依赖[37]方面实际上效率很低，而且它们的序列性质使得训练过程中不可能实现并行化。
相比之下，基于cnns的方法[20,22,25]很容易并行化。STGCN[20]和LSGCN[25]使用一维卷积[38]进行时间特征学习。Graph WaveNet[22]通过叠加多个扩张的1D卷积[39]指数级放大接收野。然而，长期的相关性将被如此稀释，以有效地利用。
基于注意力的方法[34,24,26]以并行的方式参与每个时间位置，这使它们能够胜任长期建模。

一些研究[29,24,30,26]考虑了时空异质性 。通常，

• STSGCN[29]具有针对不同时间段的多个内置模块，以捕获本地化的时空图中的异构性。
• AGCRN[30]在传统GCN的基础上增加了节点自适应参数学习模块。
• GMAN[24]在进行缩放点积方法之前将时空嵌入与特征连接起来。>
• ASTGNN[26]在输入中加入了时间嵌入和空间嵌入来引入异构性。

对于STSGCN、AGCRN和ASTGNN，考虑的异质性是相对于输入序列的，因此与内在的时间属性无关。此外，通过直接求和29,26将外部时空属性与输入(特征)融合似乎是不合理的，因为它们本质上是两种不同类型的数据。

2.2. Attention Mechanism

注意机制[12,58]最早被提出用于神经语言建模。它使查询能够自适应地参与和聚合值集合。在算法上，分配给每个值的权重是由查询的兼容函数和与该值相关的相应键计算出来的。近年来，注意力机制为许多任务带来了很大的改进，如自然语言处理[59]，图像字幕[60]，语音识别[61]和多元时间序列分析[62]。在交通领域，注意力机制在交通数据动力学建模中也显示出了其有效性。近期工作包括ASTGCN[34]、MRA-BGCN[28]、LSGCN[25]、GMAN[24]、ASTGNN[26]。

当查询queries, 键 keys 和 值values 相同时，注意力就变成了自我关注。相对于RNN和CNN，自注意作为一种序列表示学习方法，具有全局的接受域，通过并行化可以有效地执行。这些特性赋予了它强大的长序列建模能力。此外，通过使用多头注意[58]，它能够学习不同表示子空间中的相关性，使得建模更加灵活。

3. Preliminaries

3.1. Problem Formulation

在本节中，我们介绍了一些定义，并建立了交通预测问题。
Definition 1 (Traffic Network) :交通网络是一个有向图$\mathcal{G}=(V,E,A)$,其中$V=\{v_1,v_2,\cdots ,v_N\}$是$N$个节点的集合表示交通系统中的点(例如，道路传感器、路段、十字路口、地铁站)，$E$是一个有向边的集合，其中$(v_i,v_j)$表示从$v_j$指向$v_i$的有向边，$A$表示邻接矩阵：
$$A(i,j)=\{\begin{array}{ll}1,& if(v_i,v_j)\in E\\ 0,& elseotherwise\end{array}fori,j=1,\cdots ,N\text{\hspace{1em}(1)}$$

Definition 2 (Traffic States) : 节点$i$在时刻$t$的交通状态用 ${\mathcal{X}}_t^i\in R^C$,其中$C$表示featrues的number.所有节点的在时刻$t$的状态用${\mathcal{X}}_t=[{\mathcal{X}}_t^1,\cdots ,{\mathcal{X}}_t^N]\in R^{N\times C}$.

Definition 3 (Temporal Attributes): 每个时间间隔$t$附加几个时间属性，如一天中的时间、一周中的哪一天和休息日指示器。假设有$M$个可用的时态属性。时间间隔t的第$m$个属性记为$T_t^m=\{1,2,\cdots ,N_m\}$,其中，$N_m$表示可能的状态。

Definition 4 (Multiple Graphs): 基于特定的领域知识(距离、相似度等)，可以构建多个图来解释节点之间的不同关系(详见4.3.1节)。这些图被表示为$\{{\mathcal{G}}_b=(V,E_b,W_b{)}_{b=1}^B\}$,其中$E_b$表示为边集，$W_b$表示为${\mathcal{G}}_b$的权重矩阵，$B$表示graph的可能的数量。所有的图共享节点集合$V$.

Proof. 给定过去P时间间隔内的历史交通状态
$$\mathcal{X}=[{\mathcal{X}}_{t-P},{\mathcal{X}}_{t-P+1},\cdots ,{\mathcal{X}}_{t-1}]\in R^{P\times N\times C}\text{\hspace{1em}(2)}$$
在过去的$P$和下一个$H$时间间隔的时间属性
$$\mathcal{T}=[{\mathcal{T}}_{t-P}^m,{\mathcal{T}}_{t-P+1}^m,\cdots ,{\mathcal{T}}_{t+H-1}^m]\in R^{P+H}m=1,2,\cdots ,M\text{\hspace{1em}(3)}$$
以及多个预构建的图形$\{{\mathcal{G}}_b=(V,E_b,W_b{)}_{b=1}^B\}$
我们的目标是预测未来H时间间隔内的交通状态
$$\mathcal{Y}=[{\mathcal{X}}_t,{\mathcal{X}}_{t+1},\cdots ,{\mathcal{X}}_{t+N-1}]\in R^{H\times N\times C}\text{\hspace{1em}(4)}$$

3.2. Multi-Head Attention

在本节中，我们简要回顾了注意机制的概念，并引入多头注意作为理解我们方法的前提知识。

注意机制[12]可以看作是一个将查询 query 和键值对集合a collection of key-value pairs映射到输出的函数，其中查询、键和值都是向量。输出是由这些值的加权和计算出来的。分配给每个值的权重是通过一个兼容性函数计算的，其变量是查询和相应的键。

本文采用“缩放点积注意”（Scaled Dot Product Attention）[58]，通过矩阵乘法对所有查询并行执行操作。具体而言，给定查询、维度$d_k$的键和维度$d_v$的值，attention由以产生：

❓公式为什么是这个样子啊
❓查询？键？值？又分别具有什么含义呢

为了使模型能够共同出席不同的表示子空间( representation subspaces), 目前比较流行的方法是采用多头注意。让我们用$d_{model}$来表示模型的feature size。。Given the original queries $Q\in R^{n_1\times d_{model}}$ ,keys $K\in R^{n_2\times d_{model}}$ , and values $V\in R^{n_2\times d_{model}}$ ,多头注意力被计算为：

4. Meta Graph Transformer

Fig.3 (a)MGT体系结构。MGT采用编码器-解码器架构。编码器和解码器都使用跳跃连接堆叠多个子层。利用TSA、SSA和TEDA三种类型的注意层学习空间和时间相关性。所有注意层都使用STEs来执行STHA操作。SSA利用TMs进行稀疏空间注意。采用自回归方法对未来交通状态进行增量预测。(b)特定时空点$(i,t)$的STE。STE由TE和SE熔合而成。TE是从时间属性(temporal attributes)$\{{\mathcal{T}}_t^m{\}}_{m=1}^M$和序列位置$t$学习到的。SE是从交通网络的拉普拉斯特征映射学习到的。(c ) 图${\mathcal{G}}_b$的TM。首先在权重矩阵中加入自环，然后行归一化，计算出${\mathcal{G}}_b$的TM。

4.1. Overall Pipeline

该模型的主要思想是在外部时空属性的引导下，通过构建时空异质性感知(spatial - temporal heterogeneous - aware, STHA)注意层来学习复杂的时空相关性。MGT的整体架构如图3(a)所示。提出的模型具有编码器-解码器架构。
编码器和解码器 都堆叠多个相同的子层。为了提高深度神经网络的学习效率，每一个子层的输出都是跳接的，并加入到最后一个子层的输出中。在子层中，三种类型的注意层被用来学习空间和时间相关性。它们被称为时间自我注意(TSA)、空间自我注意(SSA)和时间编码器-解码器注意(TEDA)。编码器和解码器都利用TSA和SSA分别对时间和空间依赖性进行建模。解码器使用TEDAs来允许解码器中的每个位置在时间上响应输入序列中的所有位置。所有的注意层都具有多头结构，并利用从外部时空属性学习到的时空嵌入(spatial - temporal Embeddings, STs)进行STHA 操作。此外，开发 SSAs 是为了利用多个图，或者等价地利用它们的转移矩阵(TMs)，以捕获各种类型的空间相关性。为了避免解码器中的任何时间位置参与到它前面的位置，一个掩码被解码器中的所有 TSA 使用。一般情况下，MGT 模型的流程描述如下:

1. encoder的输入是历史交通数据的状态traffic state$\mathcal{X}\in R^{P\times N\times C}$.encoder使用一个带Relu函数(激活函数)的线性变换将输入映射为${\mathcal{X}}^{(0)}\in R^{P\times N\times d_{model}}$.其中$d_{model}$使我们mdoel的feature size.

线性变换+ReLU

X

X0

2. ${\mathcal{X}}^{(0)}$被喂入$l_n$个相同的encorder layers且使用skip 链接.设第$l$层的encorder layer的输出为${\mathcal{X}}^{(l)}$,最终的encoder的输出output为${\mathcal{X}}_{en}={\sum }_{l=1}^{ln}{\mathcal{X}}^{(l)},\in R^{P\times N\times d_{model}}$

X0

X1

..第l个..

Xln

X-encoder

3. 给定${\mathcal{X}}_{en}$, decoder以自回归(autoregressive)的方式预测未来交通状态。特别的，decoder 接受${\mathcal{X}}_{t-1}$真实值和之间预测的值(例如，${\hat{\mathcal{X}}}_t,\cdots ,{\hat{\mathcal{X}}}_{t+T-2}$预测值)共同作为输入。与encoder类似，decoder输入经过带有ReLU的线性变换得到具有featrue size的映射结果 (例如，$[{\mathcal{X}}_{t-1},{\hat{\mathcal{X}}}_t,\cdots ,{\hat{\mathcal{X}}}_{t+T-2}]\in R^{T\times N\times C}\to R^{T\times N\times d_{model}}$)。然后喂入$l_{de}$个decorder layers 使用skip 链接。最后，利用线性变换将特征大小映射回C，并保留最后一个时间位置的输出作为下一个时间区间${\hat{X}}_{t+T-1}\in R^{N\times C}$的预测。
4. 步骤3重复H次，逐步生成所有期望的未来交通状态(图4)。
   

Fig.4 MGT的自回归预测示例。

4.2. Spatial–Temporal Embeddings

对于特殊时空点$(i,t)$,其中$i$代表节点，$t$代表特定的时间点。一个时空嵌入(spatial–
temporal embedding) $c_t^i\in R_{model}^d$ 被构造为将该点的外部空间和时间属性编码为固定长度的向量。图3(b)说明了STE的构造。

4.2.1. Temporal Embeddings

应该注意的是，除了所有时间属性$\{T_t^m{\}}_{m=1}^M$ 附加在时间间隔t上，还有另一个动态属性——相对于输入的时间位置$pos$需要考虑。具体地，时间间隔t的 时间嵌入(TE) 按如下方式构建.

1. 每一个$T_t^m$采用独热方法编码为长度为$N_m$的向量。
2. 然后，用总共$M$个可学习矩阵将这些向量线性变换为长度为$d_{model}$向量

这两个步骤相当于将每个时间属性嵌入到一个长度为$d_{model}$向量中。
对于时间位置$pos$,其位置编码$P{E}_{pos}$是一个长度为$d_{model}$的向量。它的第$i$个坐标($0\le i\le d_{model}$)被给定为：

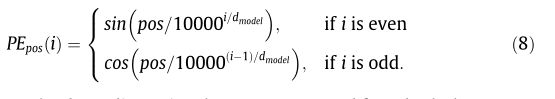
然后根据时间属性和时间位置计算出$d_{model}$维向量，并结合可学习参数进行线性变换，生成时间间隔为$t$的最终时间嵌入$U_t\in R_{model}^d$。

4.2.2. Spatial Embeddings

受[63]著作的启发，图结构信息graph structure information通过一种称为特征映射的经典图嵌入技术graph embedding technique called Eigenmaps被编码到我们的空间嵌入(SE)中[64]。为满足要求，将邻接矩阵$A$对称定义为$A_s=\max (A,A^T)$且所得到的无向图假定是连通的。然后，特征映射算法可以通过以下方式进行。

1. 首先计算归一化的拉普拉斯矩阵$L=I-D_s^{-1/2}{A}_s{D}_s^{-1/2}$，其中$D_s$是度矩阵，$I$是段位矩阵。
2. 拉普拉斯可以分解为$L=U\Lambda U^T$,其中$\Lambda =\{{\lambda }_0,\cdots ,{\lambda }_{N-1}\}$,$U=(U_0,U_1,\cdots ,U_{N-1})$是矩阵的特征向量。
3. 节点$v_i$的$k(k<N)$维嵌入被构建为${\hat{Z}}_i=[U_1(i),U_2(i),\cdots ,U_k(i)]\in R^k$。在计算特征映射后，进行可学习的线性变换来生成最终的空间嵌入$Z_i\in R_{model}^d$

4.2.3. Spatial–Temporal Embeddings

点$(i,t)$的时空嵌入$C_t^i$可以很容易地从$Z_i$和$U_t$的串联，然后是一个线性层构建。

4.3. Transition Matrices

根据后面要指定的规则，多重加权图$\{{\mathcal{G}}_b=(V,E_b,W_b){\}}_{b=1}^B$可以构造来捕获节点之间的各种类型的关系。下面，我们首先介绍三种常见图的构造，然后给出基于这些图的转移矩阵的计算。

4.3.1. Construction of Multiple Graphs

交通网络本身可以看作是一个简单的加权图，其中所有边的权值都为1。这样的图称为连通性图。给定距离信息，可以修改图的边权值，以反映节点之间的真实接近程度。$v_j$到$v_i$的基于距离的权重的一般定义为:

除了物理连通性外，功能相似性也是空间相关性探索的关键因素。虽然有些节点在现实中可能并不相连，甚至相距遥远，但在一个交通网络中(商业中心、居民区等)可能具有相同的功能，从而符合相似的交通模式。表示$X_{hist}^i\in R^{P^{\prime }C}$ 为节点$v_i$的历史流量状态($P^{\prime }$为训练集中的总时间间隔数)，定义$v_i$与$v_j$的相似度为:

通过选择相似度大于给定阈值的边，可以构造基于相似度的权值矩阵$W_{sim}$。

另一个有用的图是基于一些交通流数据集提供的源-目的地(OD)信息。典型情况下，$v_j$到$v_i$基于OD的相关性可以定义为:

其中$count(i,j)$表示从$v_j$到$v_i$的实体(车辆或人员)的总数。最终的基于OD值的权值矩阵$W_{od}$是通过选择大于阈值的边来构建的，或者通过保留每个节点的top-k出近邻来构建的。

4.3.2. Transition Matrices

给定一个加权图${\mathcal{G}}_b=(V,E_b,W_b)$,对应的转移矩阵$S_b\in R^{N\times N}$应该被下面的方式计算。

1. $W_b$的对角元素被设置为1.
2. 然后利用行归一化，计算出转移矩阵如下

4.4. Encoder

编码器通过跳跃连接将输入投影层和Len相同的编码器层堆叠起来。每个编码器层由三个组件组成，即TSA、SSA和一个前馈网络( FFN )。TSA 和 SSA 都是多头结构。它们分别负责学习时间和空间相关性。FFN 执行位置转换。在第4.2节描述的 STE 的指导下，TSA 和 SSA 能够执行 STHA 注意操作，使学习过程更适应特定的时空条件。同时，通过利用多个图，或4.3节中描述的等价的 TMs, SSA 能够从不同的角度捕捉空间相关性。这三个部分按顺序连接起来，协同学习时空表征。

4.4.1. Temporal Self-Attention

当查询queries、键key和值value为相同的向量序列，即$Q=K=V$时，3.2节中的多头注意就变成了多头自我注意。在多头自我注意直接应用于第$(l-1)$层$H^{l-1}\in R^{P\times N\times d_{model}}$的输出似乎是合理的。这相当于计算：

事实上，从式(7)可以看出，所有时间位置的参数也是共享的。这种共享机制忽略了交通状态动态随时间和地点变化较大的现象。

针对上述时间多头自注意的缺点，提出了一种STEs-guided TSA with multi-head。“‘STEs-guided”的主要思想是用相应的STEs的函数(或元知识)取代共享参数，从而将查询queries、键key和值value的学习与特定的时空条件联系起来。通过这种方式，TSA 能够进行 STHA 自我注意操作。更具体地说，为每个头部创建一个隐藏层的多层感知器:

网络生成了3个映射矩阵projection matices将$H_{t,i}^{l-1}\in R_{model}^d$分别转换为query,key and value的向量，在此基础上进行时间自我注意。此外，利用残差连接[9]和层归一化[65]使深度网络能够更好地学习。
编码器的TSA详细信息见算法1。

4.4.2. Spatial Self-Attention

与TSA相似，STEs-guided SSA with multi-head和multi-graph 被设计用于空间特征学习。使用“多重图”的直觉是，与其关注所有空间位置，不如关注那些通过领域知识更可能与中心节点相关的节点，这样更有效、更合理。因此，我们利用多个图$\{{\mathcal{G}}_b=(V,E_b,W_b){\}}_{b=1}^B$或等效的TMs $\{S_b{\}}_{b=1}^B$来捕捉不同类型的节点之间的关系，进行稀疏的自我注意。

更具体地说，对于每个图$G_b$，一个节点$v_i$将会参与它的入邻居集合$\{v_j|j\in N_i^b\}$ $N_h$次，得到$v_i$的总$B{N}_h$个向量，然后通过拼接和线性变换融合这些向量。此外，通过元素乘法，由转移矩阵中的动态注意系数和静态值共同确定分配给相邻节点的权值，从而充分利用领域知识。此外，为了保证 STHA 操作，在注意力参数的生成中利用了 STEs 。与TSA一样，这里也采用了剩余连接和层归一化。

编码器的SSA的详细信息显示在Algorithm2中。

4.4.3. Feed Forward Network

前馈网络( FNN ，图3(a))是一个位置变换层。每个时空点的参数是共享的。给定任意位置的特征向量$X\in R_{model}^d$，FFN 的表达式为:

4.5. Decoder

解码器将输出投影层output projection layer、具有跳接连接的$L_{de}$相同解码器层和用于预测的线性层堆叠起来。每个解码器层由四个组件组成，即 TSA with Mask、SSA、TEDA 和 FFN 。SSA 和 FFN 的结构与编码器中的结构相同，而 TSA 的行为通过Mask来修改，以防止任何位置参与未来的时间步长。TEDA 作为连接编码器输出和每个解码器层的桥梁，能够从历史数据中进行自适应特征学习。需要注意的是，STEs 可以被TSA with Mask 和SSA 在解码器中使用 ，它为$\{C_{t-1+s}^i|s\in \{0,\cdots ,T-1\},i\in \{1,\cdots ,N\}\}$,其中$T$表示解码器输入的时间间隔数。

4.5.1. TSA with Mask

带Mask的 TSA 工作原理与第4.4.1节中描述的TSA基本相同。唯一的区别是，一个Mask会在缩放的点积之后添加，目的是防止任何位置在时间上出现在它之前的位置❓。

Mask 设计成$T\times T$矩阵,对角线上的元素取$-\infty$，其他的取0。那么算法1中的第12行修改为:

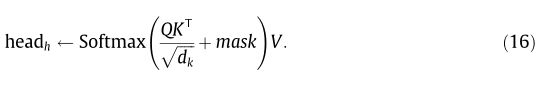
4.5.2. Temporal Encoder-Decoder Attention

创建 TEDA 用于解码器沿着时间维度自适应地参与编码特征。在这种情况下，查询queries来自解码器，而键key和值value来自编码器。通过与算法1相同的方法，可以根据编码器的输出$X_{en}\in R^{P\times N\times d_{model}}$计算出多头的键和值。keys为$\{K_{t-r,i}^h|r\in \{1,\cdots ,P\},i\in \{1,\cdots ,N\},h\in \{1,\cdots ,N_h\}\}$,Values为$\{V_{t-r,i}^h|r\in \{1,\cdots ,P\},i\in \{1,\cdots ,N\},h\in \{1,\cdots ,N_h\}\}$。这些键和值随后被解码器中的每个TEDA用来执行STEs-guided temporal attention 操作。 TEDA 的具体情况见算法3。

5. Experiments

在本节中，MGT框架和12个基线方法在三个交通数据集上实现:两个地铁人群流数据集和一个公路交通流数据集。此外，还分析了模型中关键部件和超参数的影响。

5.1. Datasets

为了验证本文提出的方法，在HZMetro、SHMetro和PEMS08三个大型交通数据集上进行了综合实验。统计信息汇总在表1中

• HZMetro[27]:该数据集来自中国杭州地铁系统。日期从2019年1月1日到2019年1月25日，我们关注的是5:30-23:30这段时间。人群流量(包括流入和流出)以15分钟的时间间隔进行聚集，一天总共有73个时间间隔。此外，我们还根据周末和节假日信息为每一天创建休息日指标。运行中的车站数量为80个。基于[27]提供的连通图和相关图，结合流量数据，采用4.3.1节中相似性阈值设置为0.1的方法，可以构建三种图。

• SHMetro [27]:该数据集建立于中国上海地铁系统，其日期涵盖2016年7月1日至2016年9月30日三个月。车站的数量是288个。与HZMetro一样，考虑了5:30-23:30这段时间，人流的时间间隔为15分钟。还为每一天创建了休息日指标，并使用与HZMetro相同的方法构建了三种类型的图表。

• PEMS08[34,29]:这是一个公路交通流数据集，收集自Caltrans (California Department of Transportation)的PeMS (Performance Measurement System)[66]。时间为2016年7月1日至2016年8月31日。将流量数据汇总到5分钟，每天有288个时间间隔。传感器的数量是170个。采用4.3.1节的方法构造基于距离的连通图和相似图，其中相似阈值设置为0.1。

5.2. Experimental Settings

在实验中，我们的目标是在给定过去一小时的交通状况的前提下，预测下一小时的交通状况。三个数据集的训练集、验证集和测试集的划分比例如表2所示。输入的特征大小为2用于HZMetro, SHMetro和1用于PEMS08。均值和标准差从训练集计算出来，用于对输入数据进行归一化。在时间属性上，城市数据集考虑了时间和休息日指标，因为城市流量受通勤影响较大，而公路数据集考虑了时间和星期。使用可用的图为所有数据集预先计算了转移矩阵，HZMetro、SHMetro的矩阵数量为3,PEMS08的矩阵数量为2。特征映射是基于k维为8的交通网络计算的。

在训练阶段，将一小时的历史数据输入编码器，以经过时间偏移的真实数据作为解码器输入，同时预测下一小时的所有状态。在测试阶段，预测是自回归的，即预测的输出将用于下一步的预测。为了衡量每种方法的性能，采用了三个指标:平均绝对误差(Mean Absolute Error, MAE)、均方根误差(Root Mean Square Error, RMSE)和平均绝对百分比误差(Mean Absolute Percentage Error, MAPE)。假设$Y=(Y_1,Y_2,\cdots ,Y_{N_s}{)}^T$表示真实值，$\hat{Y}=({\hat{Y}}_1,{\hat{Y}}_2,\cdots ,{\hat{Y}}_{N_s}{)}^T$表示预测值，其中$N_s$测试样本数量，指标定义如下:

模型特征尺寸$d_{model}$和元学习器的隐藏尺寸$d_{mt}$都设为16。在所有的注意力层中，head的次数是4。编码器和解码器分别采用6层编码器和6层解码器。为了更好的训练，在剩余连接之前，在SSA中加入概率为0.3的dropout层[67]。我们使用PyTorch[68]框架来实现我们的模型。批量大小为2，损失函数选择MAE。采用Adam[69]优化方法进行训练，初始学习率为0.001，权重衰减为0.0002。模型训练100个epoch, 50和80个epoch后学习率以0.1的比率衰减。

5.3. Baseline Methods

为了全面评估我们提出的方法的性能，我们的实验中考虑了12个基线方法。这些方法大致可以分为三类:统计模型、机器学习方法和神经网络方法。这些方法的详细情况如下:

1. 历史平均(HA):这是一种简单的季节性平均方法。周期设置为7天，使用p个周期进行预测。HZMetro的p值为2,SHMetro和PEMS08的p值为4。例如，通过平均过去的周五的相同时间间隔的数据，可以预测特定周五的7:00-7:15时间间隔的数据。
2. 支持向量回归(Support Vector Regression, SVR)[70]:该模型是支持向量分类(Support Vector Classification)用于解决回归问题的扩展。它通过最小化一个$ϵ-insensitive$损失函数和一个2范数正则化项来学习核的特征空间中的线性回归模型。每个位置都共享预测模型。Scikit-learn用于实现这种方法，我们使用径向基函数(RBF)核且设置$ϵ$为0.1。
3. 随机森林(Random Forest, RF) [71]:回归随机森林是一种元估计器，拟合多个决策树回归器，并使用平均来提高预测精度，同时控制过拟合。每个位置都共享预测模型。Scikit-learn被用来实现这个模型。我们使用整个数据集来构建每棵树，森林中的树数设置为10。
4. 向量自回归(VAR)[72]:向量自回归模型是一元自回归模型对多元时间序列数据的扩展。它允许多个时间序列之间的交互。statmodels被用来实现这个模型。
5. 前馈神经网络(FNN):采用一个隐藏层的多层感知器进行预测。该网络接收整个过去一小时内所有地点的交通数据，并预测下一小时的交通状况。隐藏大小设置为256。FNN的实现使用了PyTorch。
6. FCGRU (Fully Connected门控递归单元) :该模型采用Sequence-to-Sequence[73]架构，采用两层GRU[13]层作为递归模块。每个时间步的输入是一个NC维向量，即它包含了所有位置的特征。每一层GRU的隐藏大小为256。FCGRU的实现使用了PyTorch。
7. 扩散卷积递归神经网络(Diffusion Convolutional Recurrent Neural Network, DCRNN)[21]:该模型通过将空间相关性建模为双向图随机漫步，提出了一种图卷积运算，即扩散卷积，并将Seq2Seq框架中的矩阵乘法替换为所提出的图卷积，同时捕获时空相关性。该模型是基于其代码实现的。
8. Graph WaveNet (GWN)[22]:该Graph Wave-Net利用堆叠的扩张一维卷积组件来有效地学习时间相关性，并通过可学习的节点嵌入开发自适应依赖矩阵来捕获数据中隐藏的空间依赖性。我们基于它的代码实现这个模型。
9. Physical-Virtual Collaboration Graph Network(PVCGN)[27]:该模型将物理图和虚拟图合并到图卷积门控循环单元(GC-GRU)中学习时空表示，同时应用全连接门控循环单元(FC-GRU)捕捉全局演化趋势。这个模型是基于它的代码实现的。
10. Attention based Spatial–Temporal Graph Neural Network(ASTGNN) [26]:该模型在时间维度和空间维度上都采用了自我注意机制。在时间维度上，它通过将查询和键的投影操作替换为一维卷积来考虑本地上下文信息。在空间维度上，开发了具有自注意的动态图卷积模块。我们基于它的代码实现这个模型。
11. Adaptive Graph Convolutional Recurrent Network(AGCRN) [30]: AGCRN在传统GCN的基础上增加了节点自适应参数学习和数据自适应图生成模块，分别学习节点特有的模式和从数据中发现空间相关性。这个模型是基于它的代码实现的。
12. Long Short-term Graph Convolutional Networks(Long -term Graph Convolutional Networks, LSGCN) [25]:该模型以门控的方式集成了一种新的图关注网络cosat和GCN来获取空间特征，并采用门控的线性单元来获取时间特征。由于LSGCN的源代码是不公开的，我们根据其文章实现了该方法。

5.4. Experimental Results and Analysis

不同方法在三个流量数据集上的性能如表3所示。指标是所有时间步骤的平均值。可以看到，我们的模型在所有情况下都优于所有基线方法。在HZMetro上，MGT的RMSE、MAE、MAPE分别提高了3.23%、1.70%、1.23%，居次优。类似的改进也可以在SHMetro和PEMS08上看到，其中改善率分别为4.20%、3.58%、3.92%和0.43%、6.38%、2.09%。

图5给出了不同方法在所有数据集上的多步预测结果。为清晰起见，不显示HZMetro和SHMetro上的HA、SVR、RF、VAR 和 LSGCN 的结果，以及PEMS08上的HA的结果。与其他方法相比，MGT在所有时刻步骤中都表现出良好的性能。此外，随着时间的推移，MGT 的优势越来越明显，说明MGT具有长期预测的能力。

HA 依赖于流量数据的周周期。因此，HA的性能在很大程度上取决于数据集符合这种周期性的强度。此外，特殊事件，如假期也会影响结果。因此，HA的预测质量随数据集的不同而不同。但总的来说，结果远远不能令人满意。

与HA相比，SVR 和 RF 考虑了近期的流量数据，构建了更加复杂的模型。然而，SVR和RF对所有位置的建模都是模糊的，没有考虑空间相关性。一方面，节点之间的差异被忽略。另一方面，来自其他节点的有用信息没有得到充分利用。因此，当上述两个因素严重影响预测过程时，例如在HZMetro和SHMetro数据集中，SVR和RF就变得无能。

VAR 通过对多个时间序列构建向量自回归模型来考虑节点之间的相关性。因此，它在空间建模上比SVR和RF有一些优势，HZMetro和SHMetro可以看出这一点。但是VAR所假设的线性依赖在很大程度上限制了它在交通预测任务中的表现。

与上述方法相比，表3中基于神经网络的方法总体上表现出更好的性能。其原因在于神经网络复杂的函数形式和强大的特征提取能力。然而，网络的结构会影响特征学习的效率。

FNN 采用一层隐层的全连接结构，能够隐式学习复杂的时空相关性。在HZMetro上，模糊神经网络方法比非神经网络方法具有明显的优势。然而，模糊神经网络的有效性受到其完全忽略时间和空间结构的阻碍。在SHMetro和PEMS08上，FNN未能取得霸权，因为它努力应对更大的空间尺度和时间范围。

FCGRU 利用RNN获取时间相关性。与FNN相比，FCGRU在所有数据集上的结果都有所改善。但对空间结构的忽视限制了其整体性能。此外，由于其[58]的顺序性质，RNN在关联时间距离位置方面效率很低。DCRNN、 PVGCN 和 AGCRN 也存在这样的问题，它们都采用了RNN架构。GWN 和 LSGCN 使用一维卷积来缓解这个问题，但仍然需要叠加多层来进行长期学习。

DCRNN 利用图卷积进行空间特征提取。在SHMetro和PEMS08上，与图不可知方法相比，RMSE得分显著提高。但是一个图表似乎不足以捕捉交通网络的各种空间相关性。为了弥补这一缺陷，GWN和AGCRN都开发了一个自适应依赖矩阵来捕获隐藏的空间依赖性，而PVCGN利用多个图来考虑节点之间的不同关系。然而，在测试过程中，预构建或学习的图形仍然是静态的，这在空间相关性可能会随着时间变化的交通领域是不合适的。

STGNN 在时间和空间维度上都采用了注意机制，从而实现了训练示例中的动态相关性和并行化。然而，在ASTGNN中合并空间和时间异质性的方法相当简单——直接在输入中添加相应的位置嵌入。这种添加混淆了位置信息和交通状态的本质。此外，在不考虑全局时间属性的情况下，其时间异质性仅限于序列级别。此外，ASTGNN在一个图上执行空间注意操作，这使得它在提取空间距离依赖关系方面效率低下。

AGCRN 通过引入节点自适应参数学习模块，考虑了空间异质性。然而，特定节点的转换和学习到的空间依赖都是静态的。LSGCN通过空间门控块捕获全局和动态空间相关性。但在空间学习过程中，时间异质性仍未被考虑。此外，由于LSGCN是为一步预测而训练的，因此可能无法很好地学习时间上的依赖性。在我们的实验中，LSGCN的效率低于其他基于gnn的方法。

在上述方法中，ASTGNN的思想最接近我们提出的模型。然而，与ASTGNN不同的是，MGT通过元学习向注意层注入相关信息来引导注意机制的行为，从而考虑到空间和时间异质性。这样，MGT在保存参数的同时，可以对不同的时空点进行不同的注意操作。此外，不仅局部时间位置，还将全局时间属性集成到我们的 STEs 中，使我们的模型能够感知内在的时间异质性。此外，MGT 利用多个图来学习各种类型的空间相关性，从而充分利用领域知识。实验结果验证了该模型的优越性。

5.5. Comparison on rush hours

为了验证MGT的鲁棒性，表4和图6报告了高峰时段的结果。港珠澳地铁、上海地铁的高峰时段为早高峰07:00-09:00，晚高峰17:00-19:00。对于PEMS08，考虑06:00 - 24:00的流量。

从表4中可以看出，在高峰时段，我们的模型在所有情况下都比所有基线保持优势。在HZMetro上，MGT的RMSE、MAE、MAPE分别提高了2.29%、3.24%、3.73%，居次优。SHMetro和PEMS08的改善率分别为1.58%、3.81%、3.88%和0.22%、6.44%、0.32%。

图6显示了高峰时段所有数据集上不同方法的多步预测结果。与图5类似，为清晰起见，HZMetro和SHMetro上的 HA、SVR、RF、VAR 和 LSGCN 结果以及PEMS08上的 HA结果均未显示。从图中我们可以看到，MGT 在所有时间步长上通常优于其他基线，这表明了我们模型的稳健性。

5.6. Ablation Study

为了分析我们模型中不同成分的影响，消融研究在所有三个数据集上实施。

5.6.1. Analysis in view of Temporal and Spatial Message Passing

为了研究从时间和空间维度传递的消息的贡献，我们设计了三种模型变体:

1. MGT- noTSA:去除MGT中所有的TSA(带或不带掩膜)层，以研究时间自我注意的贡献。
2. MGT- noSSA:去除MGT中所有SSA层，研究空间自我注意的贡献
3. MGT-noMG:我们将SSA使用的图的数量减少到1个，即只使用基本连通性图。目的是证明使用多个图是合理的。

上述模型采用与 MGT 相同的设置，只是研究的组件不同。表5显示了不同变体模型下一个小时的平均得分，并将其与MGT进行比较。多步性能如图7所示。

从表5和图7可以看出，MGT- noTSA的表现不如 MGT，这表明了时间自我注意层在我们的模型中的帮助。在MGT-noSSA中也可以看到类似的分数下降，这表明来自其他位置的交通状态对于推断当前位置至关重要。与MGT-noSSA相比，MGT-noMG考虑了空间学习的图结构，从而提高了预测精度。此外，通过考虑多个图形，MGT进一步提高了预测精度。这种现象表明多个图在捕捉各种类型的空间相关性方面是有用的。

5.6.2. Analysis in view of Temporal and Spatial Heterogeneity

为了研究时空异质性对交通预测的影响，我们的模型考虑了四种变量:

1. MGT- noSTE: MGT中每一个由ste引导的注意都被传统的多头注意所取代(公式6)，从而评估考虑时空异质性的效果.
2. MGT-noTE:STEs被SEs取代，以验证考虑时间异质性的必要性。
3. MGT-noSE:将STEs替换为TEs，验证考虑空间异质性的必要性。
4. MGT- noMeta:与MGT- noSTE类似，MGT中的每一个由STEs-guided attention 都被传统的多头注意所取代。不同之处在于，STEs 是直接加入到输入中，以考察进行 STHA 注意操作的效果。

上述模型采用与MGT相同的设置，只是研究的组件不同。表6显示了所有不同模型下一个小时的平均得分，并将其与MGT进行比较。多步性能如图8所示。

MGT-noSTE的结果是我们变种中最糟糕的。通过考虑空间嵌入，MGT-noTE提高了预测精度，验证了交通数据存在空间异质性。类似的改进可以在MGT-noSE中看到，它将时间嵌入到每个注意层，表明在交通预测中考虑时间异质性的重要性。MGT noMeta通过简单的输入求和来利用时空嵌入，从而赋予模型在一定程度上区分不同时空点的能力。因此，MGT-noMeta比MGT-noSTE取得了更好的分数。通过以元学习的方式利用时空嵌入，MGT取得了最好的效果。这充分证明了STHA注意力操作的力量。

5.6.3. Analysis of Transition Matrices

为了解释转移矩阵在我们的模型中的有效性，研究了所有可用转移矩阵的可能组合。表7报告了所有时间步骤的平均度量。多步预测对比如图9所示。

可以看到，不使用任何TMs的模型(对应于5.6.1节中的MGT-noSSA)的结果是最差的。随着TMs数量的增加，大多数情况下误差会减少。当所有可用的tm都被利用(对应于 MGT )时，模型通常会获得最佳性能。这种现象验证了多个图在空间相关性学习中的有用性和有效性。

5.7. Analysis of Hyperparameters

为了进一步研究超参数的影响，我们对HZMetro进行了一系列实验。研究了4个超参数，即模型的特征大小$d_{model}$、元学习者的隐藏大小$d_{mt}$、编码器(解码器)层数L(我们设$L_{en}=L_{de}=L$)和head的数目$N_h$。除研究的超参数外，实验设置与第5.2节相同。结果如图10所示。从结果可以看出，我们的模型对超参数不敏感。

5.8. Model Size Comparison

表8列出了三个流量数据集上所有神经网络模型的模型规模(即参数个数)。作为一种考虑多图的方法，MGT的参数比PVCGN少得多。此外，MGT的大小并不随着节点数的增加而增加(HZMetro和SHMetro都是0.7 M)。此外，通过元学习，MGT能够实现STHA注意操作，同时保持经济的内存消耗。

5.9. Efficiency Study

研究了不同神经网络模型对三种交通数据集的推理效率。所有的实验都运行在相同的NVIDIA TITAN Xp GPU上。对于每个设置，我们报告推断测试样本所需的平均时间(秒)。表9总结了所有的运行时间。由表9可以看出，FNN 和 FCGRU 是最有效的模型，DCRNN、GWN、ASTGNN、AGCRN 和 LSGCN 在推断过程中花费的时间相对较多，PVGCN 花费的时间最多。MGT对HZMetro、SHMetro和PEMS08的推断时间分别为0.0129s、0.0254s和0.1819s。这意味着MGT可以在0.2秒内预测每个数据集在未来一小时内的所有位置的交通状态。总之，所有的模型都可以实时运行。为了进一步降低MGT的计算复杂度，可以考虑一种或多种模型压缩技术[74]，如参数修剪和共享、低秩分解和知识蒸馏。我们把这个留给以后研究。

6. Conclusion

在本文中，我们提出了一种新的用于时空交通预测的元图转换器框架。管理策略框架在时间维度和空间维度上均采用注意机制。对每个时空点，将外部属性嵌入为一个时空嵌入，然后由所有注意层利用外部属性进行时空异构感知注意操作。此外，利用多个图来进行稀疏的空间注意，使模型能够从不同的角度捕捉空间相关性。在三个大型交通数据集上的实验证明了该模型的优越性。

Fig5–>10

Fig.5 不同方法在HZMetro、SHMetro和PEMS08数据集上的多步预测比较.

Fig.6 不同方法在HZMetro、SHMetro和PEMS08数据集上的高峰时段多步预测比较

Fig.7 从时间和空间信息传递的角度对不同变量模型进行多步预测比较。

Fig.8 从时间和空间异质性的角度比较不同变量模型的多步预测。

Fig.9 不同转换矩阵选择的MGT变量模型的多步预测比较。

Fig.10 HZMetro超参数分析。研究的四个超参数分别是:模型的特征大小dmodel、元学习者的隐藏大小dmt、编码器(解码器)层数L和头部数Nh。第一列显示了未来一小时的平均指标，而其他三列说明了多步预测性能

---

注释区