详细介绍机器学习中的交叉验证方法

前言

在研究生阶段接触机器学习的时候，我导问我一个问题，你实验里面有用到交叉验证吗？当时我就一脸懵逼了，然后当然吞吞吐吐说有。后面赶紧补了一下交叉验证的只是以及在代码上加上。说到这，突然很怀念以前的学生食堂。废话不多说，现在总结下交叉验证的方法。机器学习的模型在训练阶段目的是希望能够学习一些参数，获得从训练集的权重和偏差的最佳值。交叉验证时一种用于估计机器学习模型性能的统计方法，它是一种评估统计分析结果如何推广到独立数据集的方法，其实简单而言就是验证模型的泛化能力。

在交叉验证中，先将训练数据分成若干个小的训练测试集，然后根据若干个训练集训练你的模型。以下是常用的交叉验证方法：

• HoldOut交叉验证
• K-Fold交叉验证
• 分层K-Fold交叉验证
• Leave P Out交叉验证
• 留一法交叉验证
• 蒙特卡罗（shuffle-split）
• 时间序列（滚动交叉验证）

HoldOut交叉验证

HoldOut将整个数据集被随机划分为训练集和验证集。根据经验，整个数据集的近 70% 用作训练集，其余 30% 用作验证集。这种方式是比较常用的。它的优点是：快速执行：因为我们必须将数据集拆分为训练集和验证集一次，并且模型将在训练集上仅构建一次，因此可以快速执行。缺点是：1. 不适合不平衡数据集：假设我们有一个不平衡数据集，它具有“0”类和“1”类。假设 80% 的数据属于“0”类，其余 20% 的数据属于“1”类。在训练集大小为 80%，测试数据大小为数据集的 20% 的情况下进行训练-测试分割。可能会发生“0”类的所有 80% 数据都在训练集中，而“1”类的所有数据都在测试集中。所以我们的模型不能很好地概括我们的测试数据，因为它之前没有看到过“1”类的数据；2. 大量数据无法训练模型。在小数据集的情况下，将保留一部分用于测试模型，其中可能具有我们的模型可能会错过的重要特征，因为它没有对该数据进行训练。

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
iris=load_iris()
X=iris.data
Y=iris.target
print("Size of Dataset {}".format(len(X)))
logreg=LogisticRegression()
x_train,x_test,y_train,y_test=train_test_split(X,Y,test_size=0.3,random_state=42)
logreg.fit(x_train,y_train)
predict=logreg.predict(x_test)
print("Accuracy score on training set is {}".format(accuracy_score(logreg.predict(x_train),y_train)))
print("Accuracy score on test set is {}".format(accuracy_score(predict,y_test)))

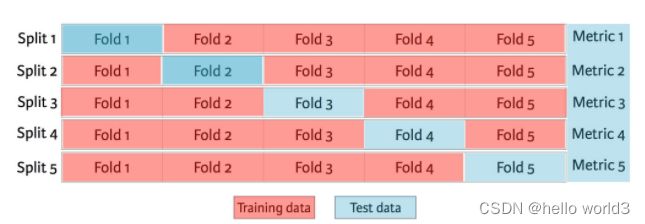
K折交叉验证

K 折交叉验证技术中，整个数据集被划分为 K 个相等大小的部分。每个分区称为一个“Folder”。一折用作验证集，其余 K-1 折用作训练集。操作过程如下所示：

1. Shuffle the dataset randomly.
2. Split the dataset into k groups
3. For each unique group:
   3.1 Take the group as a hold out or test data set
   3.2 Take the remaining groups as a training data set
   3.3 Fit a model on the training set and evaluate it on the test set
   3.4 Retain the evaluation score and discard the model
4. Summarize the skill of the model using the sample of model evaluation scores
   

K折交叉验证将整个数据集既用作训练集又用作验证集。但是不用于不平衡的数据集：正如在 HoldOut 交叉验证的情况下所讨论的，在 K-Fold 验证的情况下也可能发生训练集的所有样本都没有样本形式类“1”，并且只有 类“0”。验证集将有一个类“1”的样本；不适合时间序列数据：对于时间序列数据，样本的顺序很重要。但是在 K 折交叉验证中，样本是按随机顺序选择的。

from sklearn.datasets import load_iris
from sklearn.model_selection import cross_val_score,KFold
from sklearn.linear_model import LogisticRegression
iris=load_iris()
X=iris.data
Y=iris.target
logreg=LogisticRegression()
kf=KFold(n_splits=5)
score=cross_val_score(logreg,X,Y,cv=kf)
print("Cross Validation Scores are {}".format(score))
print("Average Cross Validation score :{}".format(score.mean()))

分层K折交叉验证

分层K-Fold(Stratified K FOLD) 是K折校验的增强版本，适用于不平衡的数据集。就像K-FOLDER一样，整个数据集被分成大小相等的K-fold。优点是能够很好地处理不平衡数据，分层交叉验证中的每个折叠都会以整个数据集中相同的比率表示所有类别的数据。缺点是不适合时间序列数据：对于时间序列数据，样本的顺序很重要。

from sklearn.datasets import load_iris
from sklearn.model_selection import cross_val_score,StratifiedKFold
from sklearn.linear_model import LogisticRegression
iris=load_iris()
X=iris.data
Y=iris.target
logreg=LogisticRegression()
stratifiedkf=StratifiedKFold(n_splits=5)
score=cross_val_score(logreg,X,Y,cv=stratifiedkf)
print("Cross Validation Scores are {}".format(score))
print("Average Cross Validation score :{}".format(score.mean()))

Leave P Out

Leave P Out 交叉验证是一种详尽的交叉验证技术，其中 p 样本用作验证集，剩余的 n-p 样本用作训练集。假设在数据集中有 100 个样本。如果使用 p=10，那么在每次迭代中，10 个值将用作验证集，其余 90 个样本将用作训练集。重复这个过程，直到整个数据集在 p 样本和 n-p 训练样本的验证集上被划分。它的优点是所有数据样本都用作训练和验证样本。缺点是1. 计算时间长：由于上述技术会不断重复，直到所有样本都用作验证集，因此计算时间会更长；2. 不适合不平衡数据集：与 K 折交叉验证相同，如果在训练集中我们只有 1 个类的样本，那么我们的模型将无法推广到验证集。

from sklearn.model_selection import LeavePOut,cross_val_score
from sklearn.datasets import load_iris
from sklearn.ensemble import RandomForestClassifier
iris=load_iris()
X=iris.data
Y=iris.target
lpo=LeavePOut(p=2)
lpo.get_n_splits(X)
tree=RandomForestClassifier(n_estimators=10,max_depth=5,n_jobs=-1)
score=cross_val_score(tree,X,Y,cv=lpo)
print("Cross Validation Scores are {}".format(score))
print("Average Cross Validation score :{}".format(score.mean()))

留一交叉验证

留一交叉验证是一种详尽的交叉验证技术，其中 1 个样本点用作验证集，其余 n-1 个样本用作训练集。假设在数据集中有 100 个样本。然后在每次迭代中，1 个值将用作验证集，其余 99 个样本作为训练集。因此，重复该过程，直到数据集的每个样本都用作验证点。它与使用 p=1 的 LeavePOut 交叉验证相同。

蒙特卡罗交叉验证

蒙特卡罗交叉验证，也称为Shuffle Split交叉验证，是一种非常灵活的交叉验证策略。在这种技术中，数据集被随机划分为训练集和验证集。我们已经决定了要用作训练集的数据集的百分比和用作验证集的百分比。如果训练集和验证集大小的增加百分比总和不是 100，则剩余的数据集不会用于训练集或验证集。假设我们有 100 个样本，其中 60% 的样本用作训练集，20% 的样本用作验证集，那么剩下的 20%( 100-(60+20)) 将不被使用。这种拆分将重复我们必须指定的“n”次。

蒙特卡罗交叉验证优点是可以自由使用训练和验证集的大小，另外可以选择重复的次数而不依赖于重复的折叠次数。但是它的缺点是可能不会为训练集或验证集选择很少的样本。不适合不平衡的数据集，在定义训练集和验证集的大小后，所有的样本都是随机选择的，所以训练集可能没有测试局中的数据类别设置，并且该模型将无法概括为看不见的数据。

from sklearn.model_selection import ShuffleSplit,cross_val_score
from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression
logreg=LogisticRegression()
shuffle_split=ShuffleSplit(test_size=0.3,train_size=0.5,n_splits=10)
scores=cross_val_score(logreg,iris.data,iris.target,cv=shuffle_split)
print("cross Validation scores:n {}".format(scores))
print("Average Cross Validation score :{}".format(scores.mean()))

时间序列交叉验证

时间序列数据是在不同时间点收集的数据。由于数据点是在相邻时间段收集的，因此观测值之间可能存在相关性。这是区分时间序列数据与横截面数据的特征之一。

在时间序列数据的情况下，我们不能选择随机样本并将它们分配给训练集或验证集，因为使用未来数据中的值来预测过去数据的值是没有意义的。由于数据的顺序对于时间序列相关问题非常重要，所以我们根据时间将数据拆分为训练集和验证集，也称为“前向链”方法或滚动交叉验证。我们从一小部分数据作为训练集开始。基于该集合，我们预测稍后的数据点，然后检查准确性。然后将预测样本作为下一个训练数据集的一部分包括在内，并对后续样本进行预测。

import numpy as np
from sklearn.model_selection import TimeSeriesSplit
X = np.array([[1, 2], [3, 4], [1, 2], [3, 4], [1, 2], [3, 4]])
y = np.array([1, 2, 3, 4, 5, 6])
time_series = TimeSeriesSplit()
print(time_series)
for train_index, test_index in time_series.split(X):
    print("TRAIN:", train_index, "TEST:", test_index)
    X_train, X_test = X[train_index], X[test_index]
    y_train, y_test = y[train_index], y[test_index]