GRU模型
GRU模型
GRU(Gated Recurrent Unit),也称门控循环单元结构,它是传统RNN的变体,同LSTM一样能够有效捕捉长序列之间的语义关联,环节梯度消失和梯度爆炸现象,同时它的结构和计算机要比LSTM更简单,他的核心结构可以分为两个部分解析:
- 更新门
- 重置门
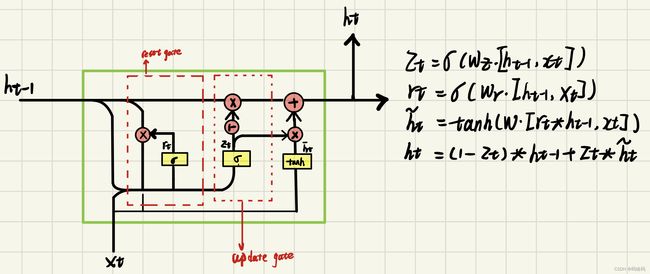
GRU的内部结构图和计算公式
内部结构分析
和之前分析过的LSTM中的门]控- -样,首先计算更新门]和重置门的门]值分别是z(的和r(t),计算方法就是使用X(t)与h(t-1)拼接进行线性变换,再经过sigmoid激活.之后更新门门值作用在了h(t-1)上,代表控制上一时间步传来的信息有多少可以被利用.接着就是使用这个更新后的h(t- 1)进行基本的RNN计算,即与x(t)拼接进行线性变化,经过tanh激活,得到新的h(t)。最后重置门的门值会作用在新的h(t),而1-门值会作用在h(t-1)上, 随后将两者的结果相加,得到最终的隐含状态输出h(t),这个过程意味着重置门有能力重置之前所有的计算,当门值趋于1时,输出就是新的h(),而当门值趋于0时,输出就是上一时间步的h(t-1)。
Bi-GRU与Bi-LSTM的逻辑相同,都是不改变其内部结构,而是将模型应用两次且方向不同,再将两次得到的LSTM结果进行拼接作为最终输出。具体参见上小节中的Bi-LSTM。
code
Pytorch中GRU工具的使用:
●位置:在torch.nn工具包之中,通过torch.nn.GRU可调用.
nn.GRU类初始化主要参数解释
●input size: 输入张量x中特征维度的大小
●hidden size: 隐层张量h中特征维度的大小
●num. _layers:隐含层的数量
●bidirectional:是否选择使用双向LSTM,如果为True,则使用;默认不使用
●nn.GRU类实例化对象主要参数解释:
●input: 输入张量x
●h0: 初始化的隐层张量h
import torch
import torch.nn as nn
#实例化GRU对象
#第一个参数: input_size(输入张量x的维度)
#第二个参数: hidden_size( 隐藏层的维度,隐藏层神经元数量)
#第三个参数: num_layers (隐藏层的层数)
gru = nn.GRU(5,6,2)
#设定输入的张量x
#第一个参数: sequence_length( 输入序列的长度)
#第二个参数: batch_size(批次的样本数)
#第三个参数: input_size(输入张量x的维度)
input = torch. randn(1,3,5)
#初始化隐藏层的张量h0
#第一个参数:num_layers*num_direction(隐藏层层数*方向数)
#第二个参数:batch_size(批次样本个数)
#第三个参数:hidden_size(隐藏层的维度)
h0 = torch. randn(2,3,6)
#将input,h0放入GRU中,得到输出张量结果
output,hn = gru(input,h0)
output
'''
tensor([[[ 0.2434, -0.1658, -0.2573, 0.4601, 0.4427, 0.1731],
[-0.0840, 0.0435, -0.0394, 0.2295, -0.5860, -0.6337],
[-0.4222, -0.6013, -0.7849, -0.8197, -0.7507, 0.7607]]],
grad_fn=)'''
output.shape
#torch.Size([1, 3, 6])
hn
'''tensor([[[ 0.0074, -0.6283, 0.2433, 0.1006, 0.8167, -0.2925],
[ 0.1320, -0.3379, 1.0510, 0.7130, -0.3881, -0.6786],
[-0.1086, -0.2509, 0.4275, 0.5853, -0.4212, -0.3319]],
[[ 0.2434, -0.1658, -0.2573, 0.4601, 0.4427, 0.1731],
[-0.0840, 0.0435, -0.0394, 0.2295, -0.5860, -0.6337],
[-0.4222, -0.6013, -0.7849, -0.8197, -0.7507, 0.7607]]],
grad_fn=)'''
hn.shape
#torch.Size([2, 3, 6])
GRU的优势
●GRU和LSTM作用相同,在捕捉长序列语义关联时,能有效抑制梯度消失或爆炸,效果都优于传统RNN且计算复杂度相比STM要小。
GRU的缺点
●GRU仍然不能完全解决梯度消失问题,同时其作用RNN的变体,有着RNN结构本身的一大弊端,即不可并行计算,这在数据量和模型体量逐步增大的未来,是RNN发展的关键瓶颈。