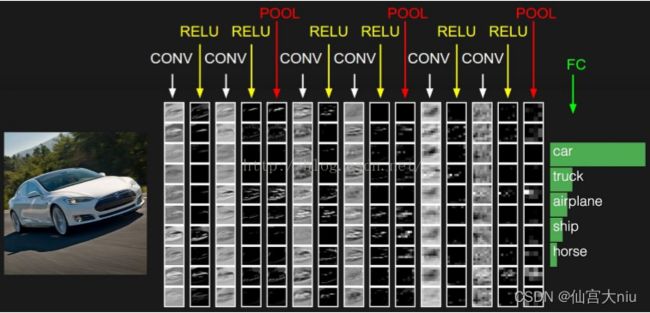
卷积神经网络(CNN)基础知识
文章目录
- 卷积神经网络基础知识
-
- 卷积与互相关
-
- 卷积
-
- 一维卷积
- 二维卷积
- 互相关
- 填充与步幅
-
- 填充
- 步幅
- 卷积神经网络结构和原理详解(见下节)
卷积神经网络基础知识
卷积神经网络(Convolutional Neural Network,CNN或ConvNet)是一种具有局部连接、权值共享等特性的深层前馈神经网络。
卷积神经网络最早主要是用来处理图像信息。在用全连接前馈网络来处理图像时,会存在以下两个问题:
- 参数太多:如果输人图像大小为100×100×3(即图像高度为100,宽度为100以及RGB 3个颜色通道),在全连接前馈网络中,第一个隐藏层的每个神经元到输入层都有100×100×3=30000个互相独立的连接,每个连接都对应一个权重参数。随着隐藏层神经元数量的增多,参数的规模也会急剧增加。这会导致整个神经网络的训练效率非常低,也很容易出现过拟合。
- 局部不变性特征:自然图像中的物体都具有局部不变性特征,比如尺度缩放、平移、旋转等操作不影响其语义信息:而全连接前馈网络很难提取这些局部不变性特征,一般需要进行数据增强来提高性能。卷积神经网络是受生物学上感受野机制的启发而提出的。感受野(Receptive Field)机制主要是指听觉、视觉等神经系统中一些神经元的特性,即神经元只接受其所支配的刺激区域内的信号。在视觉神经系统中,视觉皮层中的神经细胞的输出依赖于视网膜上的光感受器。视网膜上的光感受器受刺激兴奋时,将神经冲动信号传到视觉皮层,但不是所有视觉皮层中的神经元都会接受这些信号,一个神经元的感受野是指视网膜上的特定区域,只有这个区城内的刺激才能够激活该神经元。
目前的卷积神经网络一般是由卷积层、汇聚层和全连接层交叉堆叠而成的前馈神经网络。卷积神经网络有三个结构上的特性:局部连接、权重共享以及汇聚。这些特性使得卷积神经网络具有一定程度上的平移缩放和旋转不变性。和前馈神经网络相比,卷积神经网络的参数更少。
卷积神经网络主要使用在图像和视频分析的各种任务(比如图像分类、人脸识别、物体识别、图像分割等)上,其准确率一般也远远超出了其他的神经网络模型.近年来卷积神经网络也广泛地应用到自然语言处理、推荐系统等领域。
卷积与互相关
卷积
卷积(Convolution),是分析数学中一种重要的运算。在信号处理或者图像处理中,经常使用一维卷积或二维卷积
一维卷积
一维卷积经常用在信号处理中,用于计算信号的延迟累积,假设一个信号发生器每个时刻t产生一个信号 x t x_t xt,其信息的衰减率为 ω k ω_k ωk。即在 K − 1 K-1 K−1个时间步长后,信息为原来的 ω ω ω倍。假设 ω 1 = 1 , ω 2 = 1 / 2 , ω 3 = 1 / 4 ω_1=1,ω_2=1/2,ω_3=1/4 ω1=1,ω2=1/2,ω3=1/4,那么在时到t收到的信号,为当前时刻产生的信息和以前时刻延迟信息的叠加,
y t = 1 × x t + 1 2 × x t − 1 + 1 4 × x t − 2 = ω 1 × x t + ω 2 × x t − 1 + ω 3 × x t − 2 = ∑ k = 1 3 ω k x t − k + 1 % MathType!MTEF!2!1!+- % feaahqart1ev3aaaM9-sbqvzybssUbxD0bctH52z1f2zLbaxIv2zP5 % 2EHXwAN5wFnaciMaYE7XfDLHhD7LxF991ECrxz4r3E01xF91tmCrxA % Tv2CGS3E413x7rxF9TcxMjxyJTxm9TNm9XfDP1wzZbYE7HxFFThDTe % tF9TcxMjxyJTxm9Thn9XfDP1wzZbYE7HxFFThDTitF9bcxCbsdGyci % GaciG0ZE7X1BTv2zHbsFFTxm91hx0LwBLnhi7ThE991E01xFRS3EC9 % wBLDwyG03x7jtF9XfDP1wzZbYE7HxFFThDTetF9TYE7X1BTv2zHbsF % FT3m91hx0LwBLnhi7ThE991E01Im91hiCXfinaIjGaciGaspCnxDTX % fBP1wA0n3x7TwpX0Nx7ntF7T3EC9wBLDwyG03x7TwF913E7HxFFThD % TS2kX0xFGWfxG0axL5gz7fgBPDMB9bWexLMBbXgBcf2CPn2qVrwzqf % 2zLnharuavP1wzZbItLDhis9wBH5garmWu51MyVXgaruWqVvNCPvMC % G4uz3bqee0evGueE0jxyamXvP5wqSX2qVrwzqf2zLnharyWYoZC5ai % baieYlNi-xH8yiVC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0x % bbG8FasPYRqj0-yi0dXdbba9pGe9xq-JbbG8A8frFve9Fve9Ff0dme % aabaqaciGacaGaaeqabaWaaeaaeaqbaOabaeqabaaeaaaaaaaaa8qa % caqG5bWdamaaBaaaleaapeGaaeiDaaWdaeqaaOWdbiabg2da9iaaig % dacqGHxdaTcaWG4bWdamaaBaaaleaapeGaamiDaaWdaeqaaOWdbiab % gUcaRmaalaaapaqaa8qacaaIXaaapaqaa8qacaaIYaaaaiabgEna0k % aadIhapaWaaSbaaSqaa8qacaWG0bGaeyOeI0IaaGymaaWdaeqaaOWd % biabgUcaRmaalaaapaqaa8qacaaIXaaapaqaa8qacaaI0aaaaiabgE % na0kaadIhapaWaaSbaaSqaa8qacaWG0bGaeyOeI0IaaGOmaaWdaeqa % aaGcbaWdbiabg2da9iabeM8a39aadaWgaaWcbaWdbiaaigdaa8aabe % aak8qacqGHxdaTcaWG4bWdamaaBaaaleaapeGaamiDaaWdaeqaaOWd % biabgUcaRiabeM8a39aadaWgaaWcbaWdbiaaikdaa8aabeaak8qacq % GHxdaTcaWG4bWdamaaBaaaleaapeGaamiDaiabgkHiTiaaigdaa8aa % beaak8qacqGHRaWkcqaHjpWDpaWaaSbaaSqaa8qacaaIZaaapaqaba % GcpeGaey41aqRaamiEa8aadaWgaaWcbaWdbiaadshacqGHsislcaaI % YaaapaqabaaakeaapeGaeyypa0ZaaabCa8aabaWdbiabeM8a39aada % WgaaWcbaWdbiaadUgaa8aabeaaaeaapeGaam4Aaiabg2da9iaaigda % a8aabaWdbiaaiodaa0GaeyyeIuoakiaadIhapaWaaSbaaSqaa8qaca % WG0bGaeyOeI0Iaam4AaiabgUcaRiaaigdaa8aabeaaaaaa!0338! \begin{array}{l} {{\rm{y}}_{\rm{t}}} = 1 \times {x_t} + \frac{1}{2} \times {x_{t - 1}} + \frac{1}{4} \times {x_{t - 2}}\\ = {\omega _1} \times {x_t} + {\omega _2} \times {x_{t - 1}} + {\omega _3} \times {x_{t - 2}}\\ = \sum\limits_{k = 1}^3 {{\omega _k}} {x_{t - k + 1}} \end{array} yt=1×xt+21×xt−1+41×xt−2=ω1×xt+ω2×xt−1+ω3×xt−2=k=1∑3ωkxt−k+1
我们把 ω 1 , ω 2 , . . . ω_1,ω_2,... ω1,ω2,...称为滤波器或卷积核。假设滤波器的长度为 K K K,它和一个信号序列 x 1 , x 2 . . . x_1,x_2... x1,x2...的卷积为:
y t = ∑ k = 1 K ω k x t − k + 1 % MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbWexLMBbXgBd9gzLbvyNv2CaeHbl7mZLdGeaGqiVu0Je9sqqr % pepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs % 0-yqaqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaai % aabeqaamaabaabauaakeaacaWG5bWaaSbaaSqaaiaadshaaeqaaOGa % eyypa0ZaaabCaeaacWGNasyYdC3ai4jGBaaaleacEcOai4jGdUgaae % qcEciaaeaacaWGRbGaeyypa0JaaGymaaqaaiaadUeaa0GaeyyeIuoa % kiacEc4G4bWai4jGBaaaleacEcOai4jGdshacWGNaAOeI0Iai4jGdU % gacWGNaA4kaSIai4jGigdaaeqcEciaaaa!60AC! {y_t} = \sum\limits_{k = 1}^K {{\omega _k}} {x_{t - k + 1}} yt=k=1∑Kωkxt−k+1
为了简单起见,假设卷积的输出 y t y_t yt的下标 t t t从 K K K开始。
信号序列 x x x和滤波器 ω ω ω卷积定义为:
y = w ∗ x % MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbWexLMBbXgBd9gzLbvyNv2CaeHbl7mZLdGeaGqiVu0Je9sqqr % pepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs % 0-yqaqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaai % aabeqaamaabaabauaakeaacaWH5bGaaCypaiaahEhacGaGqFOkaiaa % hIhaaaa!44F2! {\bf{y = w*x}} y=w∗x
其中 ∗ * ∗表示卷积运算。一般情况下滤波器的长度K远小于信号序列x的长度。
我们可以设计不同的滤波器来提取信号序列的不同特征。比如,当令滤波器 ω = [ 1 / K , … , 1 / K ] ω=[1/K,…,1/K] ω=[1/K,…,1/K]时,卷积相当于信号序列的简单移动平均(窗口大小为 K K K);当令滤波器 ω = [ 1 , − 2 , 1 ] ω=[1,-2,1] ω=[1,−2,1]时,可近似对信号序列的二阶微分,即
x ′ ′ ( t ) = x ( t + 1 ) + x ( t − 1 ) − 2 x ( t ) % MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbWexLMBbXgBd9gzLbvyNv2CaeHbl7mZLdGeaGqiVu0Je9sqqr % pepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs % 0-yqaqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaai % aabeqaamaabaabauaakeaacaWG4bGaaiiyaiaaccgacaGGOaGaamiD % aiaacMcacqGH9aqpcaWG4bGaaiikaiaadshacqGHRaWkcaaIXaGaai % ykaiabgUcaRiaadIhacaGGOaGaamiDaiabgkHiTiaaigdacaGGPaGa % eyOeI0IaaGOmaiaadIhacaGGOaGaamiDaiaacMcaaaa!54F8! x''(t) = x(t + 1) + x(t - 1) - 2x(t) x′′(t)=x(t+1)+x(t−1)−2x(t)
图1,给出了两个滤波器的一维卷积示例。可以看出,两个滤波器分别提取了输入序列的不同特征。滤波器 ω = [ 1 / 3 , 1 / 3 , 1 / 3 ] ω=[1/3,1/3,1/3] ω=[1/3,1/3,1/3]可以检测信号序列中的低频信息,而滤波器 ω = [ 1 , − 2 , 1 ] ω=[1,-2,1] ω=[1,−2,1]可以检测信号序列中的高频信息。(这里的高频和低频是指信号变化的强烈程度。)

图 1 一维卷积示例(下层为输入信号序列,上层为卷积结果,边上的数字为滤波器的权重)
二维卷积
卷积也经常用在图像处理中。因为图像为一个二维结构,所以需要将一维卷积进行扩展。给定一个图像 X ∈ R M × N Χ∈R^{M×N} X∈RM×N和一个滤波器 ω ∈ R U × V \omega\in\mathbb{R}^{U\times V} ω∈RU×V,一般 ≪ , ≪ ≪,≪ U≪M,V≪N,其卷积为:
y i j = ∑ u = 1 U ∑ v = 1 V ω u v x i − u + 1 , j − v + 1 % MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbWexLMBbXgBd9gzLbvyNv2CaeHbl7mZLdGeaGqiVu0Je9sqqr % pepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs % 0-yqaqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaai % aabeqaamaabaabauaakeaacaqG5bWaaSbaaSqaaiaadMgacaWGQbaa % beaakiabg2da9maaqahabaWaaabCaeaacqaHjpWDdaWgaaWcbaGaam % yDaiaadAhaaeqaaOGaamiEamaaBaaaleaacaWGPbGaeyOeI0IaamyD % aiabgUcaRiaaigdaaeqaaOWaaSbaaSqaaiaacYcacaWGQbGaeyOeI0 % IaamODaiabgUcaRiaaigdaaeqaaaqaaiaadAhacqGH9aqpcaaIXaaa % baGaamOvaaqdcqGHris5aaWcbaGaamyDaiabg2da9iaaigdaaeaaca % WGvbaaniabggHiLdaaaa!5DC5! {{\rm{y}}_{ij}} = \sum\limits_{u = 1}^U {\sum\limits_{v = 1}^V {{\omega _{uv}}{x_{i - u + 1}}_{,j - v + 1}} } yij=u=1∑Uv=1∑Vωuvxi−u+1,j−v+1
为了简单起见,假设卷积的输出 y i j y_{ij} yij的下标 ( i , j ) \mathrm{(}i,j) (i,j)从 ( U , V ) \mathrm{(}U,V) (U,V)开始。
输入信息 X Χ X和滤波器 W W W的二维卷积定义为:
Y = W ∗ X % MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbWexLMBbXgBd9gzLbvyNv2CaeHbl7mZLdGeaGqiVu0Je9sqqr % pepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs % 0-yqaqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaai % aabeqaamaabaabauaakeaacaWGzbGaeyypa0Jaam4vaiacaIQGQaGa % amiwaaaa!4499! Y = W*X Y=W∗X
其中 ∗ * ∗表示卷积运算。
给出二维卷积示例:
假设卷积核 h \mathbf{h} h大小为 3 × 3 3\times3 3×3,待处理矩阵 x \mathbf{x} x为 5 × 5 5\times5 5×5:
h = [ 1 0 0 0 0 0 0 0 − 1 ] % MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbWexLMBbXgBd9gzLbvyNv2CaeHbl7mZLdGeaGqiVu0Je9sqqr % pepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs % 0-yqaqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaai % aabeqaamaabaabauaakeaacaWHObGaeyypa0ZaaeWaaeaafaqabeWa % daaabaGaaGymaaqaaiaaicdaaeaacaaIWaaabaGaaGimaaqaaiaaic % daaeaacaaIWaaabaGaaGimaaqaaiaaicdaaeaacqGHsislcaaIXaaa % aaGaayjkaiaawMcaaaaa!4A2E! {\bf{h}} = \left[ {\begin{matrix} 1&0&0\\ 0&0&0\\ 0&0&{ - 1} \end{matrix}} \right] h=⎣⎡10000000−1⎦⎤
x = [ 1 1 1 1 1 − 1 0 − 3 0 1 2 1 1 − 1 0 0 − 1 1 2 1 1 2 1 1 1 ] % MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbWexLMBbXgBd9gzLbvyNv2CaeHbl7mZLdGeaGqiVu0Je9sqqr % pepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs % 0-yqaqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaai % aabeqaamaabaabauaakeaacaWH4bGaeyypa0ZaaeWaaeaafaqabeqb % faaaaaqaaiaaigdaaeaacaaIXaaabaGaaGymaaqaaiaaigdaaeaaca % aIXaaabaGaeyOeI0IaaGymaaqaaiaaicdaaeaacqGHsislcaaIZaaa % baGaaGimaaqaaiaaigdaaeaacaaIYaaabaGaaGymaaqaaiaaigdaae % aacqGHsislcaaIXaaabaGaaGimaaqaaiaaicdaaeaacqGHsislcaaI % XaaabaGaaGymaaqaaiaaikdaaeaacaaIXaaabaGaaGymaaqaaiaaik % daaeaacaaIXaaabaGaaGymaaqaaiaaigdaaaaacaGLOaGaayzkaaaa % aa!58D1! {\bf{x}} = \left[{\begin{matrix} 1&1&1&1&1\\ { - 1}&0&{ - 3}&0&1\\ 2&1&1&{ - 1}&0\\ 0&{ - 1}&1&2&1\\ 1&2&1&1&1 \end{matrix}} \right] x=⎣⎢⎢⎢⎢⎡1−1201101−121−311110−12111011⎦⎥⎥⎥⎥⎤
- 将卷积核翻转 180 ° 180° 180°
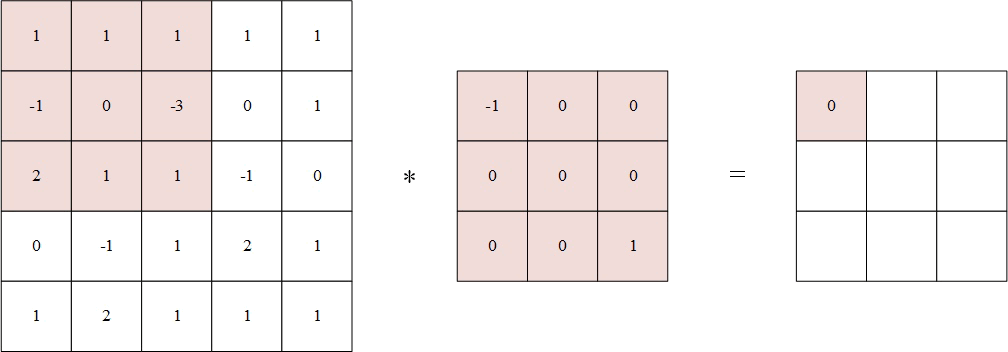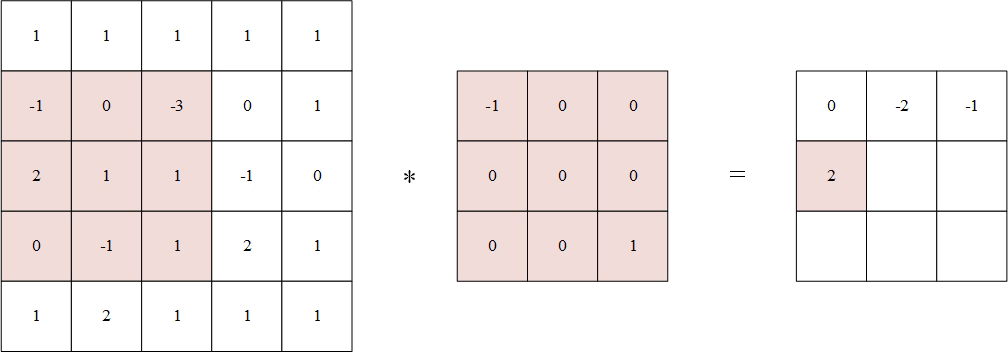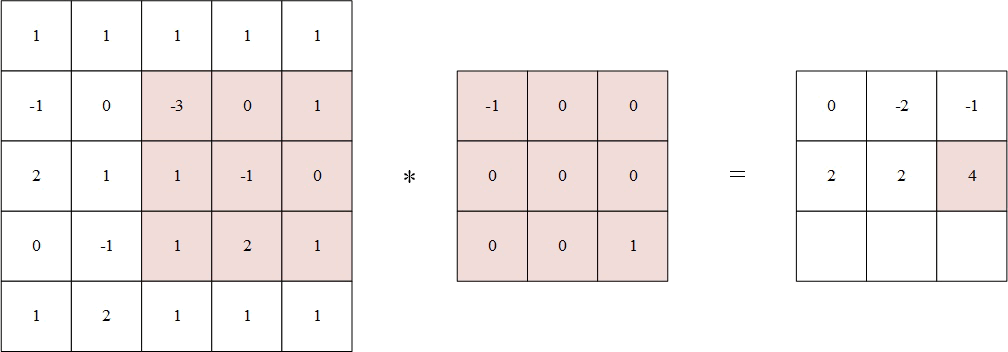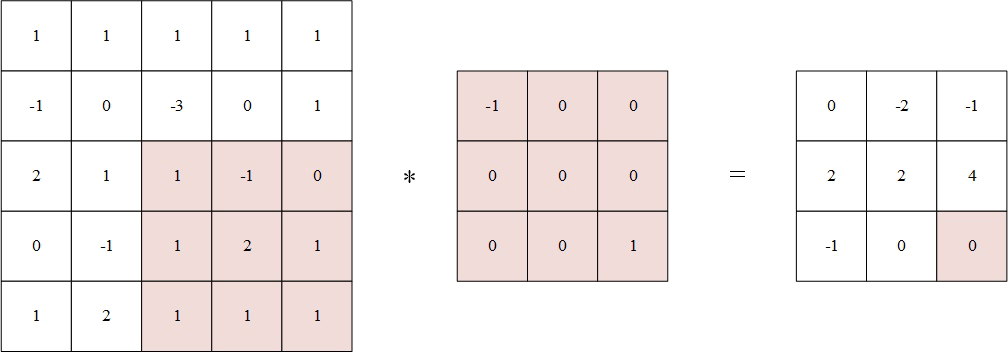
- 将翻转后的卷积核中心分别对准 X ( 2 , 2 ) Χ(2,2) X(2,2), X ( 2 , 3 ) Χ(2,3) X(2,3), X ( 2 , 4 ) Χ(2,4) X(2,4), X ( 3 , 2 ) Χ(3,2) X(3,2), X ( 3 , 3 ) Χ(3,3) X(3,3), X ( 3 , 4 ) Χ(3,4) X(3,4), X ( 4 , 2 ) Χ(4,2) X(4,2), X ( 4 , 3 ) Χ(4,3) X(4,3), X ( 4 , 4 ) Χ(4,4) X(4,4),然后对应元素相乘后相加。
例如,输出矩阵第一个值为:
1 × ( − 1 ) + 1 × 0 + 1 × 0 + ( − 1 ) × 0 + 0 × 0 + ( − 3 ) × 0 + 2 × 0 + 1 × 0 + 1 × 1 = 0 % MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbWexLMBbXgBd9gzLbvyNv2CaeHbl7mZLdGeaGqiVu0Je9sqqr % pepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs % 0-yqaqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaai % aabeqaamaabaabauaakeaacaaIXaGaey41aqRaaiikaiabgkHiTiaa % igdacaGGPaGaey4kaSIaaGymaiabgEna0kaaicdacqGHRaWkcaaIXa % Gaey41aqRaaGimaiabgUcaRiaacIcacqGHsislcaaIXaGaaiykaiab % gEna0kaaicdacqGHRaWkcaaIWaGaey41aqRaaGimaiabgUcaRiaacI % cacqGHsislcaaIZaGaaiykaiabgEna0kaaicdacqGHRaWkcaaIYaGa % ey41aqRaaGimaiabgUcaRiaaigdacqGHxdaTcaaIWaGaey4kaSIaaG % ymaiabgEna0kaaigdacqGH9aqpcaaIWaaaaa!6EB1! 1 \times ( - 1) + 1 \times 0 + 1 \times 0 + ( - 1) \times 0 + 0 \times 0 + ( - 3) \times 0 + 2 \times 0 + 1 \times 0 + 1 \times 1 = 0 1×(−1)+1×0+1×0+(−1)×0+0×0+(−3)×0+2×0+1×0+1×1=0
互相关
在机器学习和图像处理领城,卷积的主要功能是在一个图像(或某种特征)上滑动一个卷积核(即滤波器),通过卷积操作得到一组新的特征。在计算卷积的过程中,需要进行卷积核翻转。在具体实现上:一般会以互相关操作来代替卷积,从而会减少一些不必要的操作或开销,互相关(Cross-Correlation)是一衡量两个序列相关性的函数,通常是用滑动窗口的点积计算来实现.给定一个图像 X ∈ R M × N Χ∈R^{M×N} X∈RM×N和一个滤波器 ω ∈ R U × V \omega\in\mathbb{R}^{U\times V} ω∈RU×V,它们的互相关为:
y i j = ∑ u = 1 U ∑ v = 1 V ω u v x i + u − 1 , j + v − 1 % MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbWexLMBbXgBd9gzLbvyNv2CaeHbl7mZLdGeaGqiVu0Je9sqqr % pepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs % 0-yqaqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaai % aabeqaamaabaabauaakeaacaqG5bWaaSbaaSqaaiaadMgacaWGQbaa % beaakiabg2da9maaqahabaWaaabCaeaacqaHjpWDdaWgaaWcbaGaam % yDaiaadAhaaeqaaOGaamiEamaaBaaaleaacaWGPbGaey4kaSIaamyD % aiabgkHiTiaaigdaaeqaaOWaaSbaaSqaaiaacYcacaWGQbGaey4kaS % IaamODaiabgkHiTiaaigdaaeqaaaqaaiaadAhacqGH9aqpcaaIXaaa % baGaamOvaaqdcqGHris5aaWcbaGaamyDaiabg2da9iaaigdaaeaaca % WGvbaaniabggHiLdaaaa!5DC5! {{\rm{y}}_{ij}} = \sum\limits_{u = 1}^U {\sum\limits_{v = 1}^V {{\omega _{uv}}{x_{i + u - 1}}_{,j + v - 1}} } yij=u=1∑Uv=1∑Vωuvxi+u−1,j+v−1
上式可以表述为:
Y = W ⊗ X = r o t 180 ( W ) ∗ X % MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbWexLMBbXgBd9gzLbvyNv2CaeHbl7mZLdGeaGqiVu0Je9sqqr % pepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs % 0-yqaqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaai % aabeqaamaabaabauaakqaaeeqaaiaadMfacqGH9aqpcaWGxbGaey4L % IqSaamiwaaqaaiabg2da9iaadkhacaWGVbGaamiDaiaaigdacaaI4a % GaaGimaiaacIcacaWGxbGaaiykaiacaASGQaGaamiwaaaaaa!4FFD! \begin{array}{c} Y = W \otimes X\\ = rot180(W)*X \end{array} Y=W⊗X=rot180(W)∗X
其中 ⨂ \bigotimes ⨂表示互相关运算, r o t 180 ( ⋅ ) rot180(\cdot) rot180(⋅)表示旋转 180 ∘ {180}^\circ 180∘, Y ∈ R M − U + 1 , N − V + 1 Y\in\mathbb{R}^{M-U+1,N-V+1} Y∈RM−U+1,N−V+1为输出矩阵。
给出二维互相关示例:
假设卷积核 h \mathbf{h} h大小为 3 × 3 3\times3 3×3,待处理矩阵 x \mathbf{x} x为 5 × 5 5\times5 5×5:
h = [ 1 0 0 0 0 0 0 0 − 1 ] % MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbWexLMBbXgBd9gzLbvyNv2CaeHbl7mZLdGeaGqiVu0Je9sqqr % pepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs % 0-yqaqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaai % aabeqaamaabaabauaakeaacaWHObGaeyypa0ZaaeWaaeaafaqabeWa % daaabaGaaGymaaqaaiaaicdaaeaacaaIWaaabaGaaGimaaqaaiaaic % daaeaacaaIWaaabaGaaGimaaqaaiaaicdaaeaacqGHsislcaaIXaaa % aaGaayjkaiaawMcaaaaa!4A2E! {\bf{h}} = \left[ {\begin{matrix} 1&0&0\\ 0&0&0\\ 0&0&{ - 1} \end{matrix}} \right] h=⎣⎡10000000−1⎦⎤
x = [ 1 1 1 1 1 − 1 0 − 3 0 1 2 1 1 − 1 0 0 − 1 1 2 1 1 2 1 1 1 ] % MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbWexLMBbXgBd9gzLbvyNv2CaeHbl7mZLdGeaGqiVu0Je9sqqr % pepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs % 0-yqaqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaai % aabeqaamaabaabauaakeaacaWH4bGaeyypa0ZaaeWaaeaafaqabeqb % faaaaaqaaiaaigdaaeaacaaIXaaabaGaaGymaaqaaiaaigdaaeaaca % aIXaaabaGaeyOeI0IaaGymaaqaaiaaicdaaeaacqGHsislcaaIZaaa % baGaaGimaaqaaiaaigdaaeaacaaIYaaabaGaaGymaaqaaiaaigdaae % aacqGHsislcaaIXaaabaGaaGimaaqaaiaaicdaaeaacqGHsislcaaI % XaaabaGaaGymaaqaaiaaikdaaeaacaaIXaaabaGaaGymaaqaaiaaik % daaeaacaaIXaaabaGaaGymaaqaaiaaigdaaaaacaGLOaGaayzkaaaa % aa!58D1! {\bf{x}} = \left[{\begin{matrix} 1&1&1&1&1\\ { - 1}&0&{ - 3}&0&1\\ 2&1&1&{ - 1}&0\\ 0&{ - 1}&1&2&1\\ 1&2&1&1&1 \end{matrix}} \right] x=⎣⎢⎢⎢⎢⎡1−1201101−121−311110−12111011⎦⎥⎥⎥⎥⎤
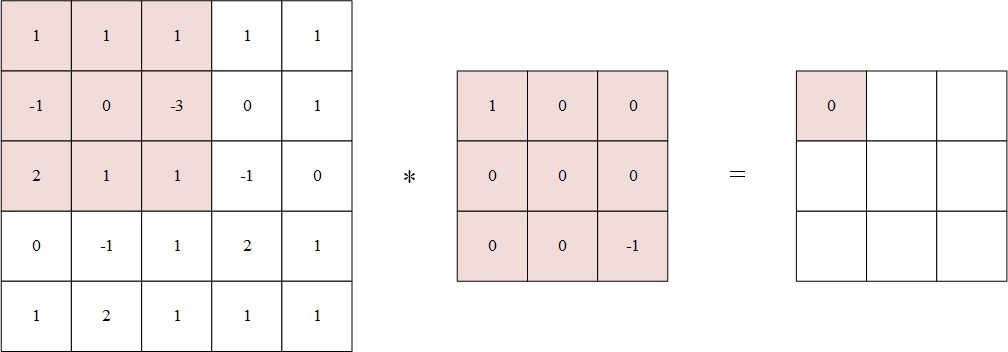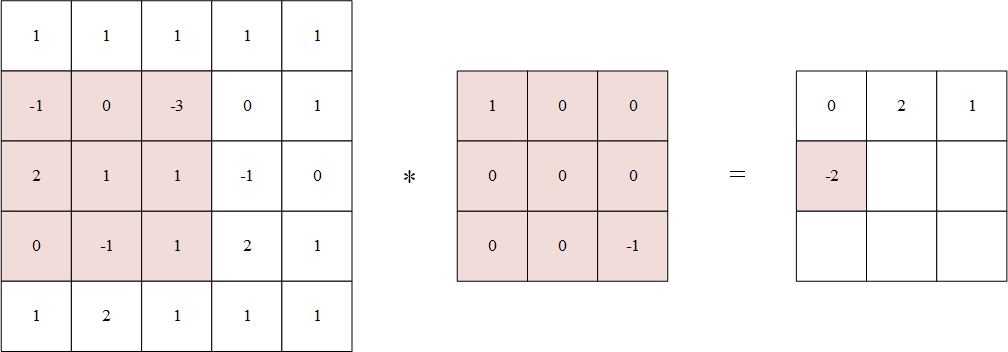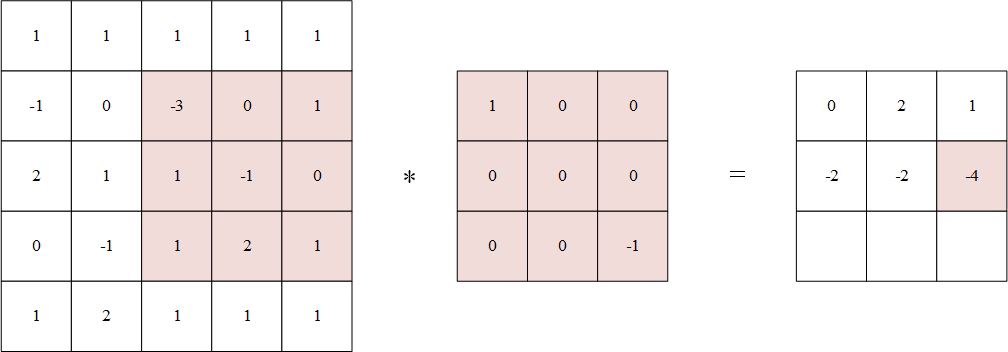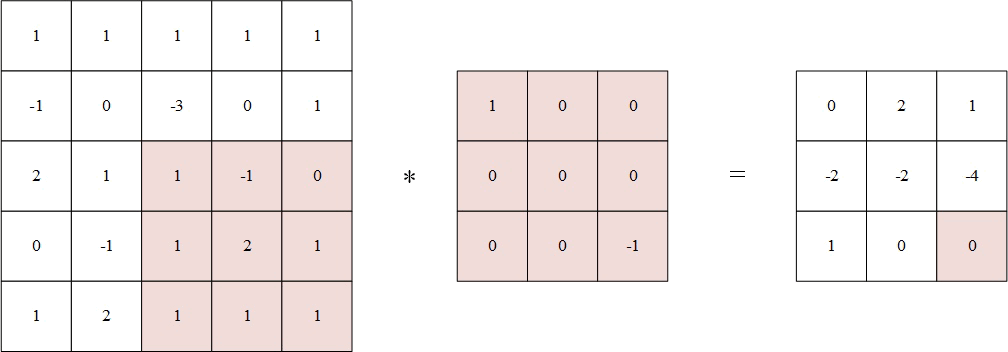
将翻转后的卷积核中心分别对准 X ( 2 , 2 ) Χ(2,2) X(2,2), X ( 2 , 3 ) Χ(2,3) X(2,3), X ( 2 , 4 ) Χ(2,4) X(2,4), X ( 3 , 2 ) Χ(3,2) X(3,2), X ( 3 , 3 ) Χ(3,3) X(3,3), X ( 3 , 4 ) Χ(3,4) X(3,4), X ( 4 , 2 ) Χ(4,2) X(4,2), X ( 4 , 3 ) Χ(4,3) X(4,3), X ( 4 , 4 ) Χ(4,4) X(4,4),然后对应元素相乘后相加。
例如,输出矩阵第一个值为:
1 × 1 + 1 × 0 + 1 × 0 + ( − 1 ) × 0 + 0 × 0 + ( − 3 ) × 0 + 2 × 0 + 1 × 0 + 1 × ( − 1 ) = 0 % MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbWexLMBbXgBd9gzLbvyNv2CaeHbl7mZLdGeaGqiVu0Je9sqqr % pepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs % 0-yqaqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaai % aabeqaamaabaabauaakeaacaaIXaGaey41aqRaaGymaiabgUcaRiaa % igdacqGHxdaTcaaIWaGaey4kaSIaaGymaiabgEna0kaaicdacqGHRa % WkcaGGOaGaeyOeI0IaaGymaiaacMcacqGHxdaTcaaIWaGaey4kaSIa % aGimaiabgEna0kaaicdacqGHRaWkcaGGOaGaeyOeI0IaaG4maiaacM % cacqGHxdaTcaaIWaGaey4kaSIaaGOmaiabgEna0kaaicdacqGHRaWk % caaIXaGaey41aqRaaGimaiabgUcaRiaaigdacqGHxdaTcaGGOaGaey % OeI0IaaGymaiaacMcacqGH9aqpcaaIWaaaaa!6EB1! 1 \times 1 + 1 \times 0 + 1 \times 0 + ( - 1) \times 0 + 0 \times 0 + ( - 3) \times 0 + 2 \times 0 + 1 \times 0 + 1 \times ( - 1) = 0 1×1+1×0+1×0+(−1)×0+0×0+(−3)×0+2×0+1×0+1×(−1)=0
在神经网络中使用卷积是为了进行特征提取,卷积核是否进行翻转和器特征提取的能力无关,特别是当卷积核是可进行学习的超参数,卷积和互相关在能力上是等价的。因此为了实现上的方便起见,使用互相关来代替卷积。事实上,很多深度学习工具中的卷积操作其实都是互相关操作。
填充与步幅
在卷积的标准定义基础上,还可以引入卷积核的零填充和滑动步长来增加卷积的多样性,可以更灵活的地进行特征提取。
填充
填充(padding)是指在输入高和宽的两侧填充元素(通常是0元素)。一般来说,假设输入形状是 n h × n w n_\mathrm{h}\times n_w nh×nw,卷积核窗口形状是 k h × k w k_\mathrm{h}\times k_w kh×kw,那么数出形状将会是 ( n h − k h + 1 ) × ( n w − k w + 1 ) {(n}_\mathrm{h}-k_\mathrm{h}+1)\times{(n}_w-k_w+1) (nh−kh+1)×(nw−kw+1)。一般来说,如果在高的两侧一共填充 p h p_\mathrm{h} ph行,在宽的两侧一共填充p_w列,那么输出的形状将会是 ( n h − k h + p h + 1 ) × ( n w − k w + p w + 1 ) {(n}_\mathrm{h}-k_\mathrm{h}+p_\mathrm{h}+1)\times{(n}_w-k_w+p_w+1) (nh−kh+ph+1)×(nw−kw+pw+1),也就是说,输出的高和宽会分别会增加 p h p_\mathrm{h} ph和 p w p_w pw。
给出填充后二维互相关运算示例:假设卷积核 h \mathbf{h} h大小为 2 × 2 2\times2 2×2,待处理矩阵 x \mathbf{x} x为 3 × 3 3\times3 3×3:
h = [ 0 1 2 3 ] % MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbWexLMBbXgBd9gzLbvyNv2CaeHbl7mZLdGeaGqiVu0Je9sqqr % pepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs % 0-yqaqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaai % aabeqaamaabaabauaakeaacaqGObGaeyypa0ZaaeWaaeaafaqabeGa % caaabaGaaGimaaqaaiaaigdaaeaacaaIYaaabaGaaG4maaaaaiaawI % cacaGLPaaaaaa!4596! {\rm{h}} = \left[ {\begin{matrix} 0&1\\ 2&3 \end{matrix}} \right] h=[0213]
x = [ 0 1 2 3 4 5 6 7 8 ] % MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbWexLMBbXgBd9gzLbvyNv2CaeHbl7mZLdGeaGqiVu0Je9sqqr % pepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs % 0-yqaqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaai % aabeqaamaabaabauaakeaacaqG4bGaeyypa0ZaaeWaaeaafaqabeWa % daaabaGaaGimaaqaaiaaigdaaeaacaaIYaaabaGaaG4maaqaaiaais % daaeaacaaI1aaabaGaaGOnaaqaaiaaiEdaaeaacaaI4aaaaaGaayjk % aiaawMcaaaaa!496E! {\rm{x}} = \left[ {\begin{matrix} 0&1&2\\ 3&4&5\\ 6&7&8 \end{matrix}} \right] x=⎣⎡036147258⎦⎤
在原输入高和宽的两侧分别添加了值为 0 0 0的元素,使得输入高和宽从 3 3 3变成了 5 5 5,并导致输出高和宽由 2 2 2增加到 4 4 4。将卷积核置于填充后的矩阵中,然后对应元素相乘后相加。
例如,输出矩阵第一个值为:
0 × 0 + 0 × 1 + 0 × 2 + 0 × 3 = 0 % MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbWexLMBbXgBd9gzLbvyNv2CaeHbl7mZLdGeaGqiVu0Je9sqqr % pepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs % 0-yqaqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaai % aabeqaamaabaabauaakeaacaaIWaGaey41aqRaaGimaiabgUcaRiaa % icdacqGHxdaTcaaIXaGaey4kaSIaaGimaiabgEna0kaaikdacqGHRa % WkcaaIWaGaey41aqRaaG4maiabg2da9iaaicdaaaa!51B7! 0 \times 0 + 0 \times 1 + 0 \times 2 + 0 \times 3 = 0 0×0+0×1+0×2+0×3=0

在很多情况下,我们会设置 p h = k h − 1 p_\mathrm{h}=k_\mathrm{h}-1 ph=kh−1和 p w = k w − 1 p_w=k_w-1 pw=kw−1来使输入和输出具有相同的高和宽。这样会方便在构造网络时推测每个层的输出形状。假设这里 k h k_\mathrm{h} kh是奇数,我们会在高的两侧分别填充 p h / 2 p_\mathrm{h}/2 ph/2行。如果 k h k_\mathrm{h} kh是偶数,一种可能是在输入的顶端一侧填充 p h / 2 p_\mathrm{h}/2 ph/2行,而在底端一侧填充 p h / 2 p_\mathrm{h}/2 ph/2行。在宽的两侧填充同理。
步幅
二维互相关运算。卷积窗口从输入数组的最左上方开始,按从左往右、从上往下的顺序,依次在输入数组上滑动。我们将每次滑动的行数和列数称为步幅(stride)。
目前我们看到的例子里,在高和宽两个方向上步幅均为 1 1 1。我们也可以使用更大步幅。高和宽步幅为 3 3 3的二维互相关运算。
给出填充后并使用新的步幅的二维互相关运算示例:假设卷积核 h \mathbf{h} h大小为 2 × 2 2\times2 2×2,待处理矩阵 x \mathbf{x} x为 3 × 3 3\times3 3×3:
h = [ 0 1 2 3 ] % MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbWexLMBbXgBd9gzLbvyNv2CaeHbl7mZLdGeaGqiVu0Je9sqqr % pepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs % 0-yqaqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaai % aabeqaamaabaabauaakeaacaqGObGaeyypa0ZaaeWaaeaafaqabeGa % caaabaGaaGimaaqaaiaaigdaaeaacaaIYaaabaGaaG4maaaaaiaawI % cacaGLPaaaaaa!4596! {\rm{h}} = \left[ {\begin{matrix} 0&1\\ 2&3 \end{matrix}} \right] h=[0213]
x = [ 0 1 2 3 4 5 6 7 8 ] % MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbWexLMBbXgBd9gzLbvyNv2CaeHbl7mZLdGeaGqiVu0Je9sqqr % pepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs % 0-yqaqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaai % aabeqaamaabaabauaakeaacaqG4bGaeyypa0ZaaeWaaeaafaqabeWa % daaabaGaaGimaaqaaiaaigdaaeaacaaIYaaabaGaaG4maaqaaiaais % daaeaacaaI1aaabaGaaGOnaaqaaiaaiEdaaeaacaaI4aaaaaGaayjk % aiaawMcaaaaa!496E! {\rm{x}} = \left[ {\begin{matrix} 0&1&2\\ 3&4&5\\ 6&7&8 \end{matrix}} \right] x=⎣⎡036147258⎦⎤
在原输入高和宽的两侧分别添加了值为 0 0 0的元素,使得输入高和宽从 3 3 3变成了 5 5 5,设置高和宽步幅为 3 3 3,并导致输出高和宽由 4 4 4减少到 2 2 2。将卷积核置于填充后的矩阵中,然后对应元素相乘后相加。
例如,输出矩阵第一个值为:
0 × 0 + 0 × 1 + 0 × 2 + 0 × 3 = 0 % MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbWexLMBbXgBd9gzLbvyNv2CaeHbl7mZLdGeaGqiVu0Je9sqqr % pepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs % 0-yqaqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaai % aabeqaamaabaabauaakeaacaaIWaGaey41aqRaaGimaiabgUcaRiaa % icdacqGHxdaTcaaIXaGaey4kaSIaaGimaiabgEna0kaaikdacqGHRa % WkcaaIWaGaey41aqRaaG4maiabg2da9iaaicdaaaa!51B7! 0 \times 0 + 0 \times 1 + 0 \times 2 + 0 \times 3 = 0 0×0+0×1+0×2+0×3=0

可以看到,输出第一列第二个元素时,卷积窗口向下滑动了 3 3 3行,而在输出第一行第二个元素时卷积窗口向右滑动了 3 3 3列。一般来说,当高的步幅为 s h \mathrm{s}_\mathrm{h} sh,宽的步幅为 s w s_w sw,输出的形状为 [ ( n h − k h + p h + s h ) / s h ] × [ ( n w − k w + p w + s w ) / s w ] {[(n}_\mathrm{h}-k_\mathrm{h}+p_\mathrm{h}+\mathrm{s}_\mathrm{h})/\mathrm{s}_\mathrm{h}]×[(nw-kw+pw+sw)/sw] [(nh−kh+ph+sh)/sh]×[(nw−kw+pw+sw)/sw]。
如果设置 p h = k h − 1 p_\mathrm{h}=k_\mathrm{h}-1 ph=kh−1和 p w = k w − 1 p_w=k_w-1 pw=kw−1,那么输出的形状为将会简化为 [ ( n h + s h − 1 ) / s h ] × [ ( n w + s w − 1 ) / s w ] {[(n}_\mathrm{h}+\mathrm{s}_\mathrm{h}-1)/\mathrm{s}_\mathrm{h}]×[(nw+sw-1)/sw] [(nh+sh−1)/sh]×[(nw+sw−1)/sw]。更进一步,如果输入的高和宽分别能被高和宽上的步幅整除,那么输出形状将为 ( n h / s h ) × ( n w / s w ) {(n}_\mathrm{h}/\mathrm{s}_\mathrm{h})\times{(n}_w/s_w) (nh/sh)×(nw/sw)。