DBnet论文笔记
整理笔记
- 原文链接:https://arxiv.org/pdf/1911.08947.pdf
- 官方代码:https://link.zhihu.com/?target=https%3A//github.com/MhLiao/DB
- 周军复现代码:https://link.zhihu.com/?target=https%3A//github.com/WenmuZhou/DBNet.pytorch
以上两个版本都是基于pytorch实现的,github上还有基于tensorflow实现的版本。
目前文字检测算法可以大致分为两类:基于回归的方法和基于分割的方法。一般基于分割的方法流程是下图蓝色箭头所示:先通过网络输出图片的文本分割结果(概率图,每个像素为是否是正样本的概率),使用预设的阈值将分割结果图转换为二值图,最后使用一些聚合的操作例如连通域将像素级的结果转换成检测结果。

从上述描述可知,因为有一个使用阈值来判定前景和背景的操作,这个操作是不可微的,所以无法使用网络将该部分流程放入到网络中训练,本文通过学习threshmap和使用可微的操作来将阈值转换放入到网络中训练。流程如上图中的红色箭头所示。
1、网络结构
标准FPN结构,不过看图,最后两个输出是由不同的输出头给出。作者在resnet的stage2-4中使用Deformable convolution来更好的检测长文本。
2、二值化
2.1标准的二值化
对于一个大小为H × W H\times WH×W(图的高为H,宽为W)的概率图P来说,使用下式来将概率图中的每个像素进行二值化:
B i , j = { 1 i f P i , j > = t 0 o t h e r w i s e B_{i,j}=\left\{ \begin{array}{rcl} 1 & & {if P_{i,j} >= t}\\ 0 & & {otherwise} \end{array} \right. Bi,j={10ifPi,j>=totherwise
上式中,t表示预设的阈值,(i, j)表示概率图中的坐标位置。输出1表示该像素为正样本也就是文字区域,输出0表示该像素为负样本也就是背景。
本文的最大创新点。在基于分割的文本检测网络中,最终的二值化map都是使用的固定阈值来获取,并且阈值不同对性能影响较大。本文中,对每一个像素点进行自适应二值化,二值化阈值由网络学习得到,彻底将二值化这一步骤加入到网络里一起训练,这样最终的输出图对于阈值就会非常鲁棒。
2.2 可微的二值化(differentiable binarization)
上述的二值化方法不可微,所以没法放入网络学习中优化。为了解决这个问题,本文提出一个近似的阶跃函数:
二值化公式如下
B ^ i , j = 1 1 + e − k ( P i , j − T i , j ) \hat{B}_{i,j} = \dfrac{1}{1+e^{-k(P_{i,j}-T_{i, j})}} B^i,j=1+e−k(Pi,j−Ti,j)1
上式输出的 B ^ \hat{B} B^ 表示近似的二值图, T T T是网络学习的阈值图, k k k是一个因子,本文设为50。该函数的图与上述的阶跃函数很近似,如下图中的a图所示。
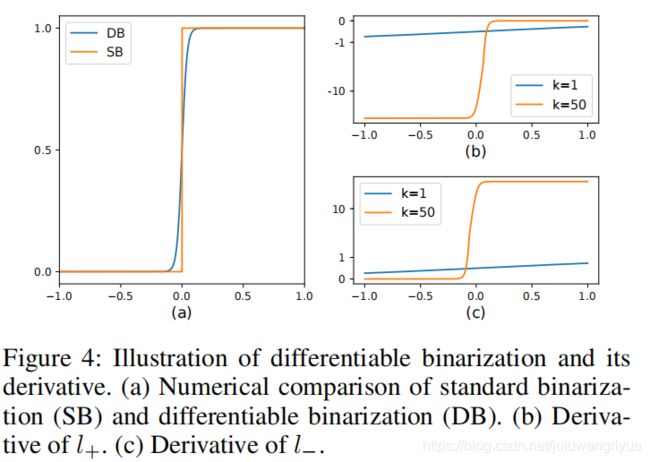
这个DB可以改善网络性能,可以从反向传播梯度方面来解释。定义 f ( x ) = 1 1 + e − k x f(x)=\dfrac{1}{1+e^{-kx}} f(x)=1+e−kx1 这里 x = P i , j − T i , j x=P_{i,j}-T_{i,j} x=Pi,j−Ti,j 就是上述定义的DB函数了。使用二值交叉熵作为loss的情况下,对于正样本的loss l + l_+ l+的计算和负样本loss l − l_- l−的计算可以表示成下面两个式子:
l + = − l o g 1 1 + e − k x l_+ =-log\dfrac{1}{1+e^{-kx}} l+=−log1+e−kx1
l − = − l o g ( 1 − 1 1 + e − k x ) l_-=-log(1 - \dfrac{1}{1+e^{-kx}}) l−=−log(1−1+e−kx1)
loss对于 x x x 的偏导数为:
∂ l + ∂ x = − k f ( x ) e − k x \dfrac{\partial l_+}{\partial x} = -kf(x)e^{-kx} ∂x∂l+=−kf(x)e−kx
∂ l − ∂ x = − k f ( x ) \dfrac{\partial l_-}{\partial x} = -kf(x) ∂x∂l−=−kf(x)
上述两个函数如图b和c 中所示,b图表示 ∂ l + ∂ x \dfrac{\partial l_+}{\partial x} ∂x∂l+,c图表示 ∂ l − ∂ x \dfrac{\partial l_-}{\partial x} ∂x∂l−。
从微分公式可以看出:
1、 k k k 是梯度的增益因子
2、梯度对于错误预测的增益幅度很大,例如当正样本被预测为负样本时,如上图中b图 x < 0 x < 0 x<0 的情况,反之亦然。
3、 自适应阈值
上面讲述了怎么在得到概率图 P P P和阈值图 T T T后,将 P P P二值化为近似二值图 B ^ \hat B B^ 。这节讲述了怎么得到概率图 P P P、阈值图 T T T、二值图 B ^ \hat B B^
的标签。
3.1、变形卷积
因为考虑到可能需要大的感受野,文章将形变卷积应用到ResNet-18或ResNet-50的网络中。
3.2、标签的生成
概率图 P P P和二值图 B ^ \hat B B^ 使用的是相同的标签。该标签的生成采用了PSENet中的生成方法。将每个标注框缩小一定的偏移量,偏移量的大小的定义如下式所示。得到的标签图称为 G s G_s Gs,原始标注文本框为 G G G
D = A ( 1 − r 2 ) L D = \dfrac{A(1 - r^2)}{L} D=LA(1−r2)
式中 L L L是标注框周长, A A A是标注框面积, r r r为预设的缩放因子,本文定义为0.4。
对于阈值图 T T T的标签生成略有差别,因为文章写的比较简洁,下面按照作者的代码来讲解。
- 首先对原始标注框 G G G,采用上述偏移量 D D D来进行扩充,得到的框为 G d G_d Gd。
- 计算框 G d G_d Gd内所有的点到 G G G的四条边的距离,选择最小的距离(也就是 G d G_d Gd框内像素离它最近的 G G G框的边的距离,下面简称像素到 G G G框的距离。)
- 将所有的 G d G_d Gd框内所有像素到 G G G框的距离,除以偏移量 D D D进行归一化。
- 将3步骤中归一化的距离限制在[0,1]内,即大于1的改为1,小于0的改为0.
- 使用1减去4中得到的map,这里得到的就是 G d G_d Gd框和 G s G_s Gs框之间的像素到 G G G框最近边的归一化距离。
- 因为这个阈值图 T T T的label,所以label不能为0和1,需要进行一定的缩放,将1缩放至0.7的值,将0缩放至0.3。
下图为上述流程求出的阈值图T,灰色的值为0.3,最白的值为0.7
4、 loss函数
本文所用的loss函数如下所示
L = L s + α × L b + β × L t L = L_s + \alpha \times L_b + \beta \times L_t L=Ls+α×Lb+β×Lt
其中 L s L_s Ls为概率图的 l o s s loss loss, L b L_b Lb为二值图的 l o s s loss loss, L t L_t Lt为阈值图的 l o s s loss loss。本文中 α \alpha α和 β \beta β分别取值为 1.0 1.0 1.0和 10 10 10。
对于 L s L_s Ls和 L b L_b Lb 采用二值交叉熵求解。
L s = L b = ∑ i ∈ S i y i l o g x i + ( 1 − y i ) l o g ( 1 − x i ) L_s= L_b= \sum_{i\in S_i}y_ilogx_i+(1-y_i)log(1-x_i) Ls=Lb=∑i∈Siyilogxi+(1−yi)log(1−xi)
式中 S i S_i Si是经过采样的数据集,正样本于负样本的比值为1:3。
对于 L t L_t Lt使用的是 L 1 l o s s L_1loss L1loss
L t = ∑ i ∈ R d ∣ y i ∗ − x i ∗ ∣ L_t=\sum_{i \in R_d}|y_i^*-x_i^*| Lt=∑i∈Rd∣yi∗−xi∗∣
式中 R d R_d Rd指的是标注框经过 D D D偏移量扩充后得到的 G d G_d Gd里的所有像素; y i ∗ y_i^* yi∗是3.2节里计算出来的阈值图的 l a b e l label label。
推理
在推理阶段,可以使用概率图也可以使用近似的二值图来生成文本区域。为了更加的高效,只使用概率图就可以了。
文本区域的生成有如下几步:
- 在概率图或者近似的二值图使用值为0.2的阈值得到二值图。
- 通过上述得到的二值图,获取文本的连通区域。
- 利用偏移量 D ′ D' D′将连通区域放大就得到了文本区域。
上述 D ′ D' D′的计算方法如下:
D ′ = A ′ × r ′ L ′ D'=\dfrac{A' \times r'}{L'} D′=L′A′×r′
式中, A ′ A' A′表示2步骤连通区域的面积, L ′ L' L′是2步骤连通区域多边形的周长, r ′ r' r′设为1.5。
参考:DBNet阅读笔记
参考:DBNet论文详解

