【算法】单词接龙,合并区间, 二叉搜索树的最近公共祖先,旋转排序数组中的最小值看看有你会的吗?
算法题目
- 一. 单词接龙 II 题目描述
-
- java 解答参考
- 二. 合并区间 题目描述
-
- java 解答参考
- 三. 二叉搜索树的最近公共祖先 题目要求
-
- java实现方案
- 四 寻找旋转排序数组中的最小值
一. 单词接龙 II 题目描述
按字典 wordList 完成从单词 beginWord 到单词 endWord 转化,一个表示此过程的 转换序列 是形式上像 beginWord -> s1 -> s2 -> … -> sk 这样的单词序列,并满足:
每对相邻的单词之间仅有单个字母不同。
转换过程中的每个单词 si(1 <= i <= k)必须是字典 wordList 中的单词。注意,beginWord 不必是字典 wordList 中的单词。 sk == endWord
给你两个单词 beginWord 和 endWord ,以及一个字典 wordList 。请你找出并返回所有从 beginWord 到 endWord 的 最短转换序列 ,如果不存在这样的转换序列,返回一个空列表。每个序列都应该以单词列表 [beginWord, s1, s2, …, sk] 的形式返回。
示例 1:
输入:beginWord = “hit”, endWord = “cog”, wordList = [“hot”,“dot”,“dog”,“lot”,“log”,“cog”]
输出:[[“hit”,“hot”,“dot”,“dog”,“cog”],[“hit”,“hot”,“lot”,“log”,“cog”]]
解释:存在 2 种最短的转换序列:
“hit” -> “hot” -> “dot” -> “dog” -> “cog”
“hit” -> “hot” -> “lot” -> “log” -> “cog”
示例 2:
输入:beginWord = “hit”, endWord = “cog”, wordList = [“hot”,“dot”,“dog”,“lot”,“log”]
输出:[]
解释:endWord “cog” 不在字典 wordList 中,所以不存在符合要求的转换序列。
提示:
1 <= beginWord.length <= 7
endWord.length == beginWord.length
1 <= wordList.length <= 5000
wordList[i].length == beginWord.length
beginWord、endWord 和 wordList[i] 由小写英文字母组成
beginWord != endWord
wordList 中的所有单词 互不相同
java 解答参考
class Solution {
public List<List<String>> findLadders(String beginWord, String endWord, List<String> wordList) {
List<List<String>> res = new ArrayList<>();
if (wordList == null)
return res;
Set<String> dicts = new HashSet<>(wordList);
if (!dicts.contains(endWord))
return res;
if (dicts.contains(beginWord))
dicts.remove(beginWord);
Set<String> endList = new HashSet<>(),
beginList = new HashSet<>();
Map<String, List<String>> map = new HashMap<>();
beginList.add(beginWord);
endList.add(endWord);
bfs(map, beginList, endList, beginWord, endWord, dicts, false);
List<String> subList = new ArrayList<>();
subList.add(beginWord);
dfs(map, res, subList, beginWord, endWord);
return res;
}
void dfs(Map<String, List<String>> map,
List<List<String>> result, List<String> subList,
String beginWord, String endWord) {
if (beginWord.equals(endWord)) {
result.add(new ArrayList<>(subList));
return;
}
if (!map.containsKey(beginWord)) {
return;
}
for (String word : map.get(beginWord)) {
subList.add(word);
dfs(map, result, subList, word, endWord);
subList.remove(subList.size() - 1);
}
}
void bfs(Map<String, List<String>> map, Set<String> beginList, Set<String> endList, String beginWord,
String endWord, Set<String> wordList, boolean reverse) {
if (beginList.size() == 0)
return;
wordList.removeAll(beginList);
boolean finish = false;
Set<String> temp = new HashSet<>();
for (String str : beginList) {
char[] charr = str.toCharArray();
for (int chI = 0; chI < charr.length; chI++) {
char old = charr[chI];
for (char ch = 'a'; ch <= 'z'; ch++) {
if (ch == old)
continue;
charr[chI] = ch;
String newstr = new String(charr);
if (!wordList.contains(newstr)) {
continue;
}
if (endList.contains(newstr)) {
finish = true;
} else {
temp.add(newstr);
}
String key = reverse ? newstr : str;
String value = reverse ? str : newstr;
if (!map.containsKey(key)) {
map.put(key, new ArrayList<>());
}
map.get(key).add(value);
}
charr[chI] = old;
}
}
if (!finish) {
if (temp.size() > endList.size()) {
bfs(map, endList, temp, beginWord, endWord, wordList, !reverse);
} else {
bfs(map, temp, endList, beginWord, endWord, wordList, reverse);
}
}
}
}
二. 合并区间 题目描述
以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间,并返回一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间。
示例 1:
输入:intervals = [[1,3],[2,6],[8,10],[15,18]]
输出:[[1,6],[8,10],[15,18]]
解释:区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2:
输入:intervals = [[1,4],[4,5]]
输出:[[1,5]]
解释:区间 [1,4] 和 [4,5] 可被视为重叠区间。
提示:
1 <= intervals.length <= 104
intervals[i].length == 2
0 <= starti <= endi <= 104
java 解答参考
class Solution {
public int[][] merge(int[][] intervals) {
List<int[]> res = new ArrayList<>();
if (intervals == null) {
return res.toArray(new int[0][]);
}
Arrays.sort(intervals, (a, b) -> a[0] - b[0]);
int i = 0;
int left = 0;
int right = 0;
while (i < intervals.length) {
left = intervals[i][0];
right = intervals[i][1];
while (i < intervals.length - 1 && right >= intervals[i + 1][0]) {
i++;
right = Math.max(right, intervals[i][1]);
}
res.add(new int[] { left, right });
i++;
}
return res.toArray(new int[0][]);
}
}
三. 二叉搜索树的最近公共祖先 题目要求
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
什么是最近公共祖先呢?百度百科解释 中将最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
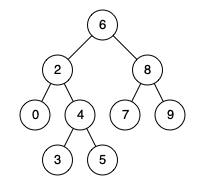
示例 1:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点
2
和节点
8
的最近公共祖先是
6
示例 2:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点
2
和节点
4
的最近公共祖先是
2
因为根据定义最近公共祖先节点可以为节点本身。
说明:
所有节点的值都是唯一的。
p、q 为不同节点且均存在于给定的二叉搜索树中。
java实现方案
所以用代码实现方式是:
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) {
val = x;
}
}
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if (p.val >= root.val && q.val >= root.val)
return lowestCommonAncestor(root.left, p, q);
else if (p.val > root.val && q.val > root.val)
return lowestCommonAncestor(root.right, p, q);
else
return root;
}
}
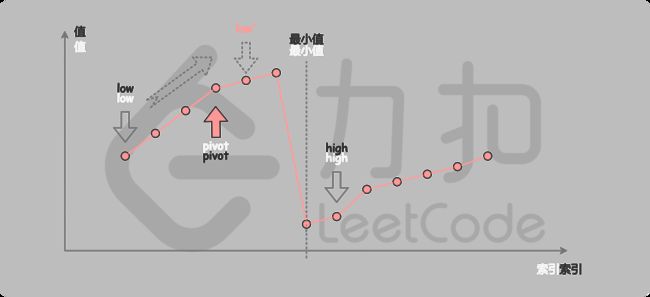
四 寻找旋转排序数组中的最小值
已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到:
若旋转 4 次,则可以得到 [4,5,6,7,0,1,2]
若旋转 7 次,则可以得到 [0,1,2,4,5,6,7]
注意,数组 [a[0], a[1], a[2], …, a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], …, a[n-2]] 。
给你一个元素值 互不相同 的数组 nums ,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。
示例 1:
输入:nums = [3,4,5,1,2]
输出:1
解释:原数组为 [1,2,3,4,5] ,旋转 3 次得到输入数组。
示例 2:
输入:nums = [4,5,6,7,0,1,2]
输出:0
解释:原数组为 [0,1,2,4,5,6,7] ,旋转 4 次得到输入数组。
示例 3:
输入:nums = [11,13,15,17]
输出:11
解释:原数组为 [11,13,15,17] ,旋转 4 次得到输入数组。
提示:
n == nums.length
1 <= n <= 5000
-5000 <= nums[i] <= 5000
nums 中的所有整数 互不相同
nums 原来是一个升序排序的数组,并进行了 1 至 n 次旋转
class Solution {
public int findMin(int[] nums) {
int low = 0, high = nums.length - 1, mid = 0;
while (low <= high) {
mid = (low + high) / 2;
if (nums[mid] > nums[high])
low = mid + 1;
else if (nums[mid] < nums[high])
high = mid;
else
high--;
}
return nums[low];
}
}