初探强化学习(13)DQN的Pytorch代码解析，逐行解析，每一行都不漏

首先上完整的代码。
这个代码是大连理工的一个小姐姐提供的。小姐姐毕竟是小姐姐，心细如丝，把理论讲的很清楚。但是代码我没怎么听懂。小姐姐在B站的视频可以给大家提供一下。不过就小姐姐这个名字，其实我是怀疑她是抠脚大汉，女装大佬。

不说了，先上完整的代码吧

1. 完整的代码

import gym
import math
import random
import numpy as np
import matplotlib.pyplot as plt
from collections import namedtuple, deque
from itertools import count
import time

import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
import torchvision.transforms as T
from torchvision.transforms import InterpolationMode


env = gym.make('SpaceInvaders-v0').unwrapped


# if gpu is to be used
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")


######################################################################
# Replay Memory

Transition = namedtuple('Transition',
                        ('state', 'action', 'next_state', 'reward'))


class ReplayMemory(object):

    def __init__(self, capacity):
        self.memory = deque([], maxlen=capacity)

    def push(self, *args):
        self.memory.append(Transition(*args))

    def sample(self, batch_size):
        return random.sample(self.memory, batch_size)

    def __len__(self):
        return len(self.memory)


######################################################################
# DQN algorithm

class DQN(nn.Module):

    def __init__(self, h, w, outputs):
        super(DQN, self).__init__()
        self.conv1 = nn.Conv2d(4, 32, kernel_size=8, stride=4)
        self.bn1 = nn.BatchNorm2d(32)
        self.conv2 = nn.Conv2d(32, 64, kernel_size=4, stride=2)
        self.bn2 = nn.BatchNorm2d(64)
        self.conv3 = nn.Conv2d(64, 64, kernel_size=3, stride=1)
        self.bn3 = nn.BatchNorm2d(64)

        def conv2d_size_out(size, kernel_size, stride):
            return (size - (kernel_size - 1) - 1) // stride  + 1
        convw = conv2d_size_out(conv2d_size_out(conv2d_size_out(w, 8, 4), 4, 2), 3, 1)
        convh = conv2d_size_out(conv2d_size_out(conv2d_size_out(h, 8, 4), 4, 2), 3, 1)
        linear_input_size = convw * convh * 64
        self.l1 = nn.Linear(linear_input_size, 512)
        self.l2 = nn.Linear(512, outputs)

    def forward(self, x):
        x = x.to(device)
        x = F.relu(self.bn1(self.conv1(x)))
        x = F.relu(self.bn2(self.conv2(x)))
        x = F.relu(self.bn3(self.conv3(x)))
        x = F.relu(self.l1(x.view(x.size(0), -1)))
        return self.l2(x.view(-1, 512))


######################################################################
# Input extraction

resize = T.Compose([T.ToPILImage(),
                    T.Grayscale(num_output_channels=1),
                    T.Resize((84, 84), interpolation=InterpolationMode.BICUBIC),
                    T.ToTensor()])


def get_screen():
    # Transpose it into torch order (CHW).
    screen = env.render(mode='rgb_array').transpose((2, 0, 1))
    screen = np.ascontiguousarray(screen, dtype=np.float32) / 255
    screen = torch.from_numpy(screen)
    # Resize, and add a batch dimension (BCHW)
    return resize(screen).unsqueeze(0)


######################################################################
# Training

# 参数和网络初始化
BATCH_SIZE = 32
GAMMA = 0.99
EPS_START = 1.0
EPS_END = 0.1
EPS_DECAY = 10000
TARGET_UPDATE = 10


init_screen = get_screen()
_, _, screen_height, screen_width = init_screen.shape

# Get number of actions from gym action space
n_actions = env.action_space.n

policy_net = DQN(screen_height, screen_width, n_actions).to(device)
target_net = DQN(screen_height, screen_width, n_actions).to(device)
target_net.load_state_dict(policy_net.state_dict())
target_net.eval()

optimizer = optim.RMSprop(policy_net.parameters())
memory = ReplayMemory(100000)

steps_done = 0


def select_action(state):
    global steps_done
    sample = random.random()
    eps_threshold = EPS_END + (EPS_START - EPS_END) * \
        math.exp(-1. * steps_done / EPS_DECAY)
    steps_done += 1
    if sample > eps_threshold:
        with torch.no_grad():
            return policy_net(state).max(1)[1].view(1, 1)
    else:
        return torch.tensor([[random.randrange(n_actions)]], device=device, dtype=torch.long)


episode_durations = []


def plot_durations():
    plt.figure(1)
    plt.clf()
    durations_t = torch.tensor(episode_durations, dtype=torch.float)
    plt.title('Training...')
    plt.xlabel('Episode')
    plt.ylabel('Duration')
    plt.plot(durations_t.numpy())
    # Take 100 episode averages and plot them too
    if len(durations_t) >= 100:
        means = durations_t.unfold(0, 100, 1).mean(1).view(-1)
        means = torch.cat((torch.zeros(99), means))
        plt.plot(means.numpy())

    plt.pause(0.001)  # pause a bit so that plots are updated


def optimize_model():
    if len(memory) < BATCH_SIZE:
        return
    transitions = memory.sample(BATCH_SIZE)
    batch = Transition(*zip(*transitions))

    # Compute a mask of non-final states and concatenate the batch elements
    # (a final state would've been the one after which simulation ended)
    non_final_mask = torch.tensor(tuple(map(lambda s: s is not None, batch.next_state)),
                                  device=device, dtype=torch.bool)
    non_final_next_states = torch.cat([s for s in batch.next_state if s is not None])
    state_batch = torch.cat(batch.state)
    action_batch = torch.cat(batch.action)
    reward_batch = torch.cat(batch.reward)

    state_action_values = policy_net(state_batch).gather(1, action_batch)
    next_state_values = torch.zeros(BATCH_SIZE, device=device)
    next_state_values[non_final_mask] = target_net(non_final_next_states).max(1)[0].detach()
    expected_state_action_values = (next_state_values * GAMMA) + reward_batch

    # Compute Huber loss
    criterion = nn.MSELoss()
    loss = criterion(state_action_values, expected_state_action_values.unsqueeze(1))

    # Optimize the model
    optimizer.zero_grad()
    loss.backward()
    for param in policy_net.parameters():
        param.grad.data.clamp_(-1, 1)
    optimizer.step()


def random_start(skip_steps=30, m=4):
    env.reset()
    state_queue = deque([], maxlen=m)
    next_state_queue = deque([], maxlen=m)
    done = False
    for i in range(skip_steps):
        if (i+1) <= m:
            state_queue.append(get_screen())
        elif m < (i + 1) <= 2*m:
            next_state_queue.append(get_screen())
        else:
            state_queue.append(next_state_queue[0])
            next_state_queue.append(get_screen())

        action = env.action_space.sample()
        _, _, done, _ = env.step(action)
        if done:
            break
    return done, state_queue, next_state_queue


######################################################################
# Start Training

num_episodes = 10000
m = 4
for i_episode in range(num_episodes):
    # Initialize the environment and state
    done, state_queue, next_state_queue = random_start()
    if done:
        continue

    state = torch.cat(tuple(state_queue), dim=1)
    for t in count():
        reward = 0
        m_reward = 0
        # 每m帧完成一次action
        action = select_action(state)

        for i in range(m):
            _, reward, done, _ = env.step(action.item())
            if not done:
                next_state_queue.append(get_screen())
            else:
                break
            m_reward += reward

        if not done:
            next_state = torch.cat(tuple(next_state_queue), dim=1)
        else:
            next_state = None
            m_reward = -150
        m_reward = torch.tensor([m_reward], device=device)

        memory.push(state, action, next_state, m_reward)

        state = next_state
        optimize_model()

        if done:
            episode_durations.append(t + 1)
            plot_durations()
            break

    # Update the target network, copying all weights and biases in DQN
    if i_episode % TARGET_UPDATE == 0:
        target_net.load_state_dict(policy_net.state_dict())
        torch.save(policy_net.state_dict(), 'weights/policy_net_weights_{0}.pth'.format(i_episode))


print('Complete')
env.close()
torch.save(policy_net.state_dict(), 'weights/policy_net_weights.pth')

2. 逐个函数的解析

2.1 定义Replay Memary

改代码中使用具名元组namedtuple()定义一个Transition ，用于存储agent与环境交互的(s,a,r,s_)

Transition = namedtuple('Transition',('state', 'action', 'next_state', 'reward'))

这个具名元组很简单
举个例子：

Student = namedtuple('Student', ('name', 'gender'))
s = Student('小花', '女')#给属性赋值

# 属性访问,有多种方法访问属性
第一种方法
print(s.name)
print(s.gender)
'''
小花
女
'''
第二种方法
print(s[0])
print(s[1])
'''
小花
女
'''
还可以迭代
for i in s:
    print(i)
'''
小花
女
'''

2.2 ReplayMemory

class ReplayMemory(object):
    def __init__(self, capacity):
        self.memory = deque([], maxlen=capacity)#deque是为了实现插入和删除操作的双向列表，适用于队列和栈：
    def push(self, *args):
        self.memory.append(Transition(*args))
    def sample(self, batch_size):
        return random.sample(self.memory, batch_size)#使用random.sample从memory中随机抽取batch_size个数据
    def __len__(self):
        return len(self.memory)

• def init(self, capacity)没啥好说的，就是定义一个双向列表。
• def push(self, *args)就是向memory中添加Transition，这个memary是一个列表，后面会详解。
• def sample(self, batch_size)是随机采样。random.sample(）其中的第一个参数是即将被采样的列表，第二个参数采样的批次。这个大家应该都懂。后面我也有例子。

2.3 DQN algorithm

class DQN(nn.Module):
    def __init__(self, h, w, outputs):
        super(DQN, self).__init__()
        self.conv1 = nn.Conv2d(4, 32, kernel_size=8, stride=4)#设置第一个卷积层
        self.bn1 = nn.BatchNorm2d(32)#设置第一个卷积层的偏置
        self.conv2 = nn.Conv2d(32, 64, kernel_size=4, stride=2)#设置第二个卷积层
        self.bn2 = nn.BatchNorm2d(64)#设置第2个卷积层的偏置
        self.conv3 = nn.Conv2d(64, 64, kernel_size=3, stride=1)#设置第3个卷积层
        self.bn3 = nn.BatchNorm2d(64)#设置第3个卷积层的偏置
        def conv2d_size_out(size, kernel_size, stride):
            return (size - (kernel_size - 1) - 1) // stride  + 1
        convw = conv2d_size_out(conv2d_size_out(conv2d_size_out(w, 8, 4), 4, 2), 3, 1)#，输入84 宽  7
        convh = conv2d_size_out(conv2d_size_out(conv2d_size_out(h, 8, 4), 4, 2), 3, 1)#，输入84 高  7
        linear_input_size = convw * convh * 64
        #计算最终的尺寸，因为最后的feature map的尺寸是7*7*64，如果拉长为1*n,则是7*7*64 = 3136
        self.l1 = nn.Linear(linear_input_size, 512)#这边就是先从3136到512.也就是全连接层的神经元的个数，说实话，这个方法好low
        self.l2 = nn.Linear(512, outputs)#最后模型输出为2，两个动作么。

    def forward(self, x):
        x = x.to(device)
        x = F.relu(self.bn1(self.conv1(x)))#用激活函数处理C1
        x = F.relu(self.bn2(self.conv2(x)))#用激活函数处理C2
        x = F.relu(self.bn3(self.conv3(x)))#用激活函数处理C3
        x = F.relu(self.l1(x.view(x.size(0), -1)))#将第3次卷积的输出拉伸为一行
        return self.l2(x.view(-1, 512))#-1表示不知道数据由多少行，但是直到最后的数据一定是512列

这是一个常规的使用pytorch搭建网络模型的框架，相信大家都懂。而且我在里面也注释了。
需要注意的一点是：

• def conv2d_size_out(size, kernel_size, stride)：这个其实就是求最后一个卷积层的feature map的尺寸。这个DQN输入的是8484的图像，按照上面的代码，最后一层的feature map的尺寸就是77，一共64个。这样做只是为了和第一个全连接层衔接一下。其实吧，这样做感觉有点多余，正常的代码用flatten()就可以了。关于如何拉平feature map，大家可以看看其他方法。
• 运行下面代码查看，当只有两个动作时，这个网络的输出。我一开始以为网络的输出应该也是按照批次来的，也就是说当模型使出32个批次的两个动作的q值应该是这个样的：[32,1,2].也就说是应该是32个1行两列的。但是实际上，是[32，2].即32行两列。这样就能解释代码的结构了。但是当我把模型拆开了之后才发现

class DQN(nn.Module):
    def __init__(self, h, w, outputs):
        super(DQN, self).__init__()
        self.conv1 = nn.Conv2d(4, 32, kernel_size=8, stride=4)#设置第一个卷积层
        self.bn1 = nn.BatchNorm2d(32)#设置第一个卷积层的偏置
        self.conv2 = nn.Conv2d(32, 64, kernel_size=4, stride=2)#设置第二个卷积层
        self.bn2 = nn.BatchNorm2d(64)#设置第2个卷积层的偏置
        self.conv3 = nn.Conv2d(64, 64, kernel_size=3, stride=1)#设置第3个卷积层
        self.bn3 = nn.BatchNorm2d(64)#设置第3个卷积层的偏置

        def conv2d_size_out(size, kernel_size, stride):
            return (size - (kernel_size - 1) - 1) // stride  + 1
        convw = conv2d_size_out(conv2d_size_out(conv2d_size_out(w, 8, 4), 4, 2), 3, 1)#，输入84 宽  7
        convh = conv2d_size_out(conv2d_size_out(conv2d_size_out(h, 8, 4), 4, 2), 3, 1)#，输入84 高  7
        linear_input_size = convw * convh * 64
        #计算最终的尺寸，因为最后的feature map的尺寸是7*7*64，如果拉长为1*n,则是7*7*64 = 3136
        self.l1 = nn.Linear(linear_input_size, 512)#这边就是先从3136到512.也就是全连接层的神经元的个数，说实话，这个方法好low
        self.l2 = nn.Linear(512, outputs)#最后模型输出为2，两个动作么。

    def forward(self, x):
        #x = x.to(device)
        x = F.relu(self.bn1(self.conv1(x)))#用激活函数处理C1
        x = F.relu(self.bn2(self.conv2(x)))#用激活函数处理C2
        x = F.relu(self.bn3(self.conv3(x)))#用激活函数处理C3
        x = F.relu(self.l1(x.view(x.size(0), -1)))#将第3次卷积的输出拉伸为一行
        return self.l2(x.view(-1, 512))#-1表示不知道数据由多少行，但是直到最后的数据一定是512列

policy_net = DQN(84, 84, 2)#Q
x = torch.rand(32,4,84, 84)

xout = policy_net(x)

print(xout.size())
#[32，2]
print(xout)

tensor([[ 3.4981e-02,  3.1048e-02],
        [ 1.4112e-01, -5.2676e-02],
        [-3.3868e-01,  3.9583e-02],
        [ 7.5908e-02, -1.2230e-01],
        [ 1.4027e-01, -1.7528e-02],
        [-1.0966e-02,  6.2111e-02],
        [-2.2511e-02, -6.1829e-02],
        [ 3.2599e-02, -8.9155e-02],
        [ 9.7833e-02, -5.0325e-02],
        [-6.4633e-02, -8.8093e-02],
        [-4.3771e-02,  1.5452e-01],
        [-1.7478e-01, -1.3224e-01],
        [ 1.9658e-02,  8.1575e-03],
        [-1.6989e-01, -6.6487e-03],
        [-1.6566e-01, -1.0833e-01],
        [-9.5961e-02,  1.1235e-02],
        [ 1.0005e-01, -1.1150e-02],
        [ 1.8165e-02,  9.9491e-03],
        [-2.3947e-01,  9.7802e-02],
        [-5.2116e-02,  4.8583e-02],
        [ 2.2504e-02,  3.8262e-04],
        [-1.1822e-01, -2.0696e-01],
        [-1.4129e-01, -1.9254e-01],
        [-2.2170e-01, -1.2232e-01],
        [ 3.3542e-02,  3.3005e-03],
        [ 1.5150e-01,  1.5330e-01],
        [-2.3675e-01, -2.4939e-01],
        [-1.0502e-01,  7.2696e-02],
        [-1.3213e-01,  1.5113e-01],
        [ 6.1988e-02,  2.5367e-02],
        [-4.2924e-01, -4.0167e-02],
        [ 5.1474e-02,  2.6885e-01]], grad_fn=<AddmmBackward0>)

2.4 图像预处理

resize = T.Compose([T.ToPILImage(),
                    T.Grayscale(num_output_channels=1),
                    T.Resize((84, 84), interpolation=InterpolationMode.BICUBIC),
                    T.ToTensor()])

#Compose法是将多种变换组合在一起。在这个步骤中，有Resize，灰度处理，
#ToTensor将PILImage转变为torch.FloatTensor的数据形式
#ToPILImage将shape为(C,H,W)的Tensor或shape为(H,W,C)的numpy.ndarray转换成PIL.Image，值不变

2.5 截屏函数

def get_screen():
    #截取游戏的屏幕，用于做训练数据的状态
    # Transpose it into torch order (CHW).
    screen = env.render(mode='rgb_array').transpose((2, 0, 1))
    #env.render扮演图像引擎的作用，以便直观地显示当前环境。transpose将图像的通道数换到最前面
    screen = np.ascontiguousarray(screen, dtype=np.float32) / 255
    #ascontiguousarray函数将一个内存不连续存储的数组转换为内存连续存储的数组，使得运行速度更快。
    screen = torch.from_numpy(screen)#即 从numpy.ndarray创建一个张量。
    # Resize, and add a batch dimension (BCHW)
    return resize(screen).unsqueeze(0)#在第0维度增加一个维度，让图像从chw变成bchw。其中b表示批次

2.6 超参数

# 参数和网络初始化
BATCH_SIZE = 32#从transition提取样本的批次大小
GAMMA = 0.99#衰减系数
EPS_START = 1.0#贪婪参数初始值
EPS_END = 0.1#贪婪参数最小值
EPS_DECAY = 10000#贪婪参数变化次数
TARGET_UPDATE = 10#target net更新次数
init_screen = get_screen()#采集游戏画面，尺寸[32,4,84,84],第一个是批次的大小，第二个图像数量，最后两个是图像尺寸
_, _, screen_height, screen_width = init_screen.shape#得到画面的尺寸：宽高
n_actions = env.action_space.n#获取游戏的动作空间，左右两个
#初始化模型
policy_net = DQN(screen_height, screen_width, n_actions).to(device)#Q
target_net = DQN(screen_height, screen_width, n_actions).to(device)#T
target_net.load_state_dict(policy_net.state_dict())#初始阶段target net和main net是一样的参数
target_net.eval()#表示步更新，只评估输出。
optimizer = optim.RMSprop(policy_net.parameters())#使用RMSprop优化网络
memory = ReplayMemory(100000)#定义经验池的容量capacity
steps_done = 0

这边没什么可说的，大家都看得懂。

policy_net = DQN(screen_height, screen_width, n_actions).to(device)#Q
target_net = DQN(screen_height, screen_width, n_actions).to(device)#T

这两句我师妹问过我是什么意思
这个其实就是初始化模型。只是作者在写这个代码的时候还有其他参数，因此需要带参初始化。
正常情况，我们写一个模型时，初始化没这么麻烦。

2.7 选择动作的函数

#动作选择函数，首先看的就是探索和开发的阈值系数 eps[0，1]
def select_action(state):
    global steps_done
    sample = random.random()## 产生 0 到 1 之间的随机浮点数
    eps_threshold = EPS_END + (EPS_START - EPS_END) * \
        math.exp(-1.*steps_done / EPS_DECAY)#最小到0.427
    steps_done += 1
    if sample > eps_threshold:#判断是随即动作还是最优动作
        #sample是(0，1)，eps_threshold越来越小，一开始是选择最优策略（开发）
        with torch.no_grad():#torch.no_grad()一般用于神经网络的推理阶段, 表示张量的计算过程中无需计算梯度
            return policy_net(state).max(1)[1].view(1, 1)#使用最优动作
    else:
        #到后期会越来越趋向于（探索），u而就是随机选择一个动作。
        return torch.tensor([[random.randrange(n_actions)]], device=device, dtype=torch.long)#随机选择动作
#random.randrange（N）在0-N之间随机生成一个数，N是动作空间数

• 这边主要解释一下这个控制eps变量的eps_threshold
  其实这是一个单调递减函数，我把这个函数的曲线画出来了。按照作者的意思，这个eps_threshold的最小值时0.427.看下图
  
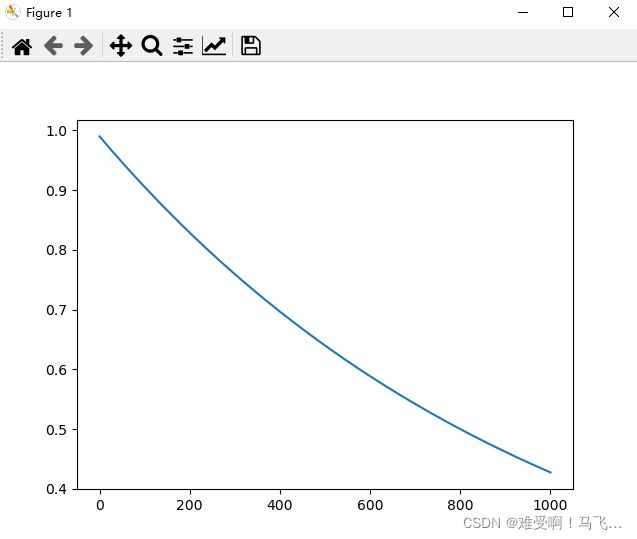
  大家可以按照下面的函数自己运行一下：
  需要提醒的是，我们可以在这个函数里的i后面乘以一个数来控制eps_threshold的最小值。
  比如我把在i后面乘以2，那么eps_threshold数值会下降2倍。

plt.figure(1)
ax = plt.subplot(111)
x = np.linspace(0, 1000, 1000)  # 在0到2pi之间，均匀产生200点的数组
print(x)
r1 = []
for i in range(1000):
    r = 0.1 + (0.99 - 0.1) * \
        math.exp(-1.*(i / 1000))
    r1.append(r)
print(r1)
ax.plot(x, r1)
plt.show()

2.8 画图函数

episode_durations = []#存储训练过程数据的列表
def plot_durations():
    plt.figure(1)
    plt.clf()#清除当前图形及其所有轴，但保持窗口打开，以便可以将其重新用于其他绘图。有了这个再次运行就不要关掉所有figure了
    durations_t = torch.tensor(episode_durations, dtype=torch.float)#转换成张量。
    plt.title('Training...')#图的名字
    plt.xlabel('Episode')#x轴坐标名
    plt.ylabel('Duration')#y轴坐标名
    plt.plot(durations_t.numpy())#画图
    # Take 100 episode averages and plot them too
    if len(durations_t) >= 100:
        means = durations_t.unfold(0, 100, 1).mean(1).view(-1)
        means = torch.cat((torch.zeros(99), means))
        plt.plot(means.numpy())

    plt.pause(0.001)  # pause a bit so that plots are updated

这个没啥说的

2.9 优化器

def optimize_model():
    if len(memory) < BATCH_SIZE:#查看记忆池是否存满
        return
    transitions = memory.sample(BATCH_SIZE)#从记忆池中随即采集BATCH_SIZE个样本
    batch = Transition(*zip(*transitions))#zip表示交叉元素，*号代表拆分
    # Compute a mask of non-final states and concatenate the batch elements
    # 计算非最终状态的掩码并连接批处理元素
    # (a final state would've been the one after which simulation ended)
    # 最终的状态应该是模拟结束后的状态
    non_final_mask = torch.tensor(tuple(map(lambda s: s is not None, batch.next_state)),device=device, dtype=torch.bool)
    #首先分析map()函数，labbda是一个简单的函数。把transition中的next_state赋值给s。
    #tuple()将状态转换为元组，元组是无法修改的
    non_final_next_states = torch.cat([s for s in batch.next_state if s is not None])
    state_batch  = torch.cat(batch.state) #合并batch中的状态 32个,竖着合并到一起尺寸是：[32，[s]]
    action_batch = torch.cat(batch.action)#合并batch中的动作,竖着合并到一起尺寸是：[32，[a]]
    reward_batch = torch.cat(batch.reward)#合并batch中的奖励,竖着合并到一起尺寸是：[32，[r]]
    
    #然后将这些数据，首先是state_batch按批次送到网络中，
    #策略函数输入状态:image，输出一个，512列的张量。在批处理中，应该是[32，1，512]
    state_action_values = policy_net(state_batch).gather(1, action_batch)#列号变动，因为是512列
    next_state_values = torch.zeros(BATCH_SIZE, device=device)#32维的张量
    next_state_values[non_final_mask] = target_net(non_final_next_states).max(1)[0].detach()
    #按行求最大值，并提取对应的最大值。
    expected_state_action_values = reward_batch + (next_state_values * GAMMA)#更新状态值函数

    # Compute Huber loss
    criterion = nn.MSELoss()
    loss = criterion(state_action_values, expected_state_action_values.unsqueeze(1))#计算损失函数

    # Optimize the model
    optimizer.zero_grad()
    loss.backward()
    for param in policy_net.parameters():
        param.grad.data.clamp_(-1, 1)
    optimizer.step()

来了，来了。我之前跟学生讲课的时候经常说，向看懂一个代码，一个算法。一定要搞清楚他们数据的流向，以及数据尺寸的变换流程。
然后第一块需要详细了解代码，这两块代码跟上面两个说会在后面讲是一块的。我需要举个例子。

    transitions = memory.sample(BATCH_SIZE)#从记忆池中随即采集BATCH_SIZE个样本
    batch = Transition(*zip(*transitions))#zip表示交叉元素，*号代表拆分

首先第一行是从memory中随机抽取一批样本，我们默认是32.。
然后就是下面的batch了。我们具体举个例子，一看便知。

import torch
import random
from collections import namedtuple, deque
#创建一个双向数组，队列长度是100。跟上面一样的
memory = deque([], maxlen=100)
#定义我们的Transition 。跟上面一样的
Transition = namedtuple('Transition',('state', 'action', 'next_state', 'reward'))
#给Transition 实例化
s1 = Transition(2,3,4,5)
s2 = Transition(1,2,3,4)
s3 = Transition(1,4,5,2)
s4 = Transition(2,5,7,3)
#然后赋值给memory
memory.append(s1)
memory.append(s2)
memory.append(s3)
memory.append(s4)
print(memory)
#原始的memory是这样的
#deque([Transition(state=2, action=3, next_state=4, reward=5), Transition(state=1, action=2, next_state=3, reward=4), Transition(state=1, action=4, next_state=5, reward=2), Transition(state=2, action=5, next_state=7, reward=3)], maxlen=100)
#随机采样2个批次
m2 = random.sample(memory, 2)
#采样后是这样的
#[Transition(state=1, action=4, next_state=5, reward=2), Transition(state=2, action=3, next_state=4, reward=5)]
#来了来了，
batch = Transition(*zip(*m2))
print(batch)
#Transition(state=(1, 2), action=(4, 3), next_state=(5, 4), reward=(2, 5))
#batch = Transition(*zip(*transitions))这句代码的一些列操作为了把单个的s,a,r,s_都给合并到一起。
#接着上面的代码，我们逐行下下看数据的变换格式
non_final_mask = torch.tensor(tuple(map(lambda s: s is not None, batch.next_state)), dtype=torch.bool)
print(non_final_mask)
#输出的是：tensor([True, True])
#也就是说，这个non_final_mask生成的是bool型变量，判断该状态是不是最终状态。

下面面大家按照这个转换格式，就知道最后走势如何处理的了。
下面看一下这个语句

    state_action_values = policy_net(state_batch).gather(1, action_batch)#列号标动，因为是2列

这个gather其实不是理解的聚集。
而类似与Qtable中的查表。计算的是Q值

• policy_net(state_batch)这部分输入的是48484的图像，输出的是一个3212的张量，表示动作Q值。32是批次
• .gather(1, action_batch)，参考这个博客。
• 主要是gather中的这个action_batch，这个变量是动作标号。
  解释这个模块目前来讲直接解释还是有点困难，因为它是在很多前处理之后的。
  我们先向下看：

2.10 随机开始

def random_start(skip_steps=30, m=4):
    env.reset()#重新初始化函数，智能体每进行一次尝试到达终止状态后，都要重新开始再尝试，所以需要智能体有重新初始化功能。
    state_queue = deque([], maxlen=m)     #  当前状态    m等于4表示采集四张图像，每采集4帧会跳30帧
    next_state_queue = deque([], maxlen=m)#下一个状态
    done = False#done又是是否结束
    for i in range(skip_steps):
        if (i+1) <= m:   #i
            state_queue.append(get_screen())#则向状态序列中继续添加图像
        elif m < (i + 1) <= 2*m:#如果大于4张，小于8张，
            next_state_queue.append(get_screen())#则将这些图像保存到下一个状态
        else:
            state_queue.append(next_state_queue[0])
            #否则的话就是大于8张，就是大于两个状态的，把上一个nextstate中的图像放到这个当前的state_queue
            next_state_queue.append(get_screen())
            #把当前的图像继续存放到下一个状态中。
            #由于两个状态容器都是用deque（）的方式，因此

        action = env.action_space.sample()#采集一个动作
        _, _, done, _ = env.step(action)#输入动作action，输出为：下一步状态，立即回报，是否终止，调试信息
        if done:
            break
    return done, state_queue, next_state_queue

2.11 开始训练

# Start Training

num_episodes = 10000
m = 4  #4张图像S
for i_episode in range(num_episodes):#迭代10000次
    # Initialize the environment and state初始化环境和状态
    done, state_queue, next_state_queue = random_start()
    if done:
        continue
    state = torch.cat(tuple(state_queue), dim=1)#状态转换成元组
    for t in count():
        reward = 0
        m_reward = 0
        # 每m帧完成一次action
        action = select_action(state)#根据当前状态选择一个动作。
        for i in range(m):
            _, reward, done, _ = env.step(action.item())#与环境交互获取奖励和是否终止
            if not done:#如果不是终止状态，则
                next_state_queue.append(get_screen())#采集图像添加到下一个状态
            else:#如果是终止状态（者打完），就跳出循环
                break
            m_reward += reward#增加奖励

        if not done:#如果没有结束，
            next_state = torch.cat(tuple(next_state_queue), dim=1)
        else:#如果结束，
            next_state = None#没有下一个状态，表示是死亡
            m_reward = -150#那么奖励直接-150
        m_reward = torch.tensor([m_reward], device=device)
        memory.push(state, action, next_state, m_reward)#将这个环节的transition添加memary中
        state = next_state#将这个nextstate更新为当前状态
        optimize_model()#开始优化模型

        if done:#如果结束了，
            episode_durations.append(t + 1)#将过程数据添加到列表中
            plot_durations()#画图
            break

    # Update the target network, copying all weights and biases in DQN
    if i_episode % TARGET_UPDATE == 0:#怕那段是否达到指定步骤，到达指定步骤则更新target
        target_net.load_state_dict(policy_net.state_dict())
        torch.save(policy_net.state_dict(), 'weights/policy_net_weights_{0}.pth'.format(i_episode))#保存模型


print('Complete')
env.close()#关闭环境
torch.save(policy_net.state_dict(), 'weights/policy_net_weights.pth')

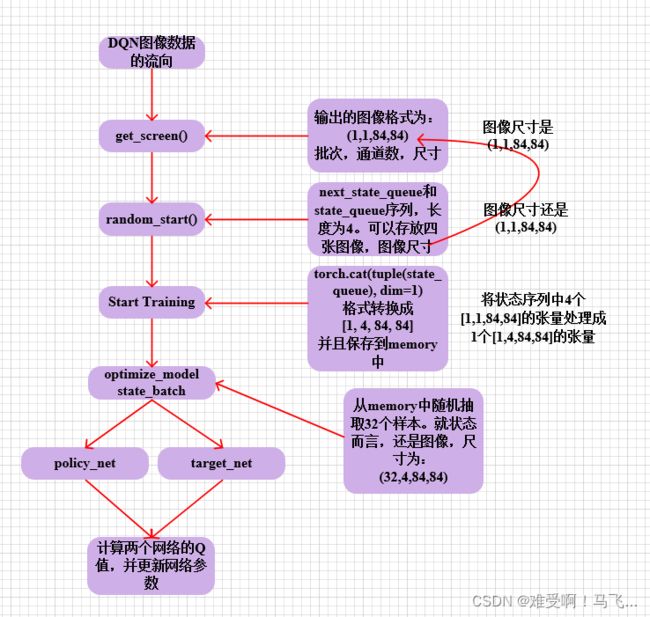
详细细节大家直接运行代码可能会很麻烦
我自己写了个效地demo来验证数据的流程了

import random
import torch
from collections import namedtuple, deque

state_que = deque([], maxlen=4)

memory = deque([], maxlen=100)
Transition = namedtuple('Transition',('state', 'action', 'next_state', 'reward'))
st1 = torch.rand(2,2)
st2 = torch.rand(2,2)
st3 = torch.rand(2,2)
st4 = torch.rand(2,2)

a1 = torch.ones(1)
a2 = torch.ones(1)
a3 = torch.ones(1)
a4 = torch.ones(1)

#模拟截屏代码get_screen，并将其处理成(1,1,84,84)的格式，在本文中，我是用图像格式为2*2
nst1 = torch.rand(2,2)#unsqueeze(0)
nst1 = nst1.unsqueeze(0)
nst1 = nst1.unsqueeze(0)
nst2 = torch.rand(2,2)
nst2 = nst2.unsqueeze(0)
nst2 = nst2.unsqueeze(0)
nst3 = torch.rand(2,2)
nst3 = nst3.unsqueeze(0)
nst3 = nst3.unsqueeze(0)
nst4 = torch.rand(2,2)
nst4 = nst4.unsqueeze(0)
nst4 = nst4.unsqueeze(0)

#将相应的变量添加到Transition中
s1 = Transition(st1,a1,nst1,5)
s2 = Transition(st2,a2,nst2,4)
s3 = Transition(st3,a3,nst3,2)
s4 = Transition(st4,a4,nst4,3)
#添加到state_que中
state_que.append(nst1)
state_que.append(nst2)
state_que.append(nst3)
state_que.append(nst4)
print('state_que',state_que)
#转换成元组
print('转换成元组和拼接')
state = torch.cat(tuple(state_que), dim=1)
print('state',state)
print('statesize',state.size())


memory.append(s1)
memory.append(s2)
memory.append(s3)
memory.append(s4)

#print(memory)


m2 = random.sample(memory, 2)
print('m2',m2)
print()
batch = Transition(*zip(*m2))
print('zip*-----------------------')
print('batch:000',batch.state)
non_final_mask = torch.tensor(tuple(map(lambda s: s is not None, batch.state)), dtype=torch.bool)
print(non_final_mask)
state_batch  = torch.cat(batch.next_state)
print('next_state_batch',state_batch)
print('state_batch_size = ',state_batch.size())
action_batch = torch.cat(batch.action)
print('action_batch',action_batch)

---

2022年11月11日更新

真特么神了，神特么的脆弱的DQN

DQN越学越倒退是什么原因

我想用通俗的语言去解释这件事情，当然也可以用非常专业的术语去解释这件事情。通俗的解析 ：强化学习非常依赖于一开始遇到的数据，特别是负反馈数据。因为如果一开始都遇到非常一般的数据，接下来的一段时间内都遇倒更差的数据，那么Agnet就会认为那些很一般的数据就是好的样本，需要去学习和保持的样本数据，后来即使Agent遇到更好的数据，它仍然有时间差分的惯性规则，继续保持一般样本的数据形态。这就像一个闭塞的糟老头一样不停别人劝谏，总是坐井观天，然后埋怨这个埋怨那个，但是不去踏出一步改变自己。专业的解析：强化学习对初始化和训练过程的动态变化都很敏感，因为数据总是在线采集的，可以执行的唯一监督只有关于奖励的变量。强化学习在较好的训练样例上，可能会更快更好地学习到较优的策略。如果没有在恰当的时机遇到好的训练样本，有可能给策略带来崩溃式的灾难，从而无法学习到好的策略，因为强化学习模型越来越相信，任何偏离现有状况的行动都有可能导致更多的负反馈。

另一种解决方案。

RL问题在全局可观测的条件下，用数字去表示输入是没有问题的。但是有时候我们希望agent只能观测一部分环境，并且对此作出响应。这时候就必须把观测做独热编码。独热编码和非独热相比有一些直观的好处。一是独热代表的是逻辑，这点是很符合神经网络的，因为神经网络的基本元素就是感知机。二是非独热有时候输入的数据会有一些线性或非线性相关性的时候，会对神经网络产生影响，神经网络可能训练的越来越发散。当然独热也有不好的一面，独热首先就没法处理连续输入。如果把连续输入离散独热化，又会让输入的数据特别庞大。所以，在做RL的人需要自己去取舍。