lecture 8：OLS回归模型

先学习这个资料：

OLS自编算法，不调用函数

重要的英文参考资料：

Using Python for Introductory Econometrics

kevinsheppard讲授Python做计量

相关分析

1.相关系数的计算公式：
$$r=\frac{\sum (x_i-\bar{x})(y_i-\bar{y})}{\sum (x_i-\bar{x}{)}^2\sum (y_i-\bar{y}{)}^2}$$
2. 统计量：
$$t=\frac{r\ast \sqrt{n-2}}{\sqrt{1-r^2}}，自由度：（n-2）$$
3.根据 t 统计量来计算显著性水平，从而确认$(x,y)$之间的相关性是否显著（$H0$：相关系数等于0，即相关性不显著）。

import pandas as pd
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.linear_model import LinearRegression


data=pd.DataFrame()
data=pd.DataFrame(pd.read_excel(r"D:\myfolder\al5-1.xls"))
x=np.array(data[['adv']])
y=np.array(data[['sale']])

plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
#matplotlib画图中中文显示会有问题，需要这两行设置默认字体
 
plt.xlabel('X')
plt.ylabel('Y')
colors1 = '#00CED1' #点的颜色
area = np.pi * 16**2  # 点面积 
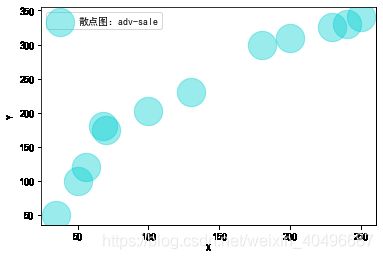
plt.scatter(x, y, s=area, c=colors1, alpha=0.4, label='散点图：adv-sale')
plt.plot(linewidth = '0.5',color='#000000')
plt.legend()
print(type(x)) #
x=np.squeeze(x)
y=np.squeeze(y)
corr,pval=stats.pearsonr(x,y)
print( '相关系数（pearson 间隔量表） = %6.5f  显著性水平 = %6.5f' % (corr, pval))

corr,pval=stats.spearmanr(x,y)
print( '相关系数（spearman 顺序量表） = %6.5f  显著性水平 = %6.5f' % (corr, pval))

相关系数（pearson ） = 0.96368 显著性水平 = 0.00000
相关系数（spearman） = 0.99301 显著性水平 = 0.00000

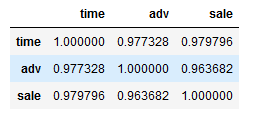
计算相关系数表

df=data[['time','adv','sale']]
df.corr()

利用现有数据回归一下：

import statsmodels.api as sm #最小二乘
from statsmodels.formula.api import ols #加载ols模型

lm=ols('sale~ adv',data=data).fit()
print(lm.summary())

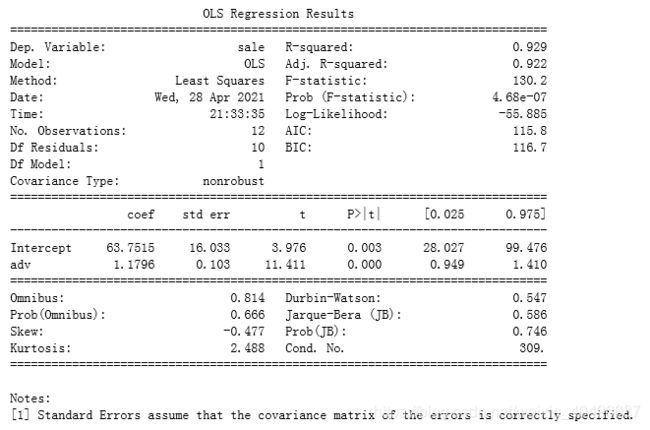
请看看上面的结果，相关系数（pearson ） = 0.96368，它的平方等于 0.9286791423999999，然后再看看上面的回归结果，$R^2$=0.929。这也验证了在二元回归方程中：$R^2=r^2$。

例子：

import statsmodels.formula.api as smf
model = smf.ols('distress ~ num_at_risk + launch_temp + leak_check_pressure + order', data = data)
result = model.fit()
# result.summary()
import matplotlib.pyplot as plt
plt.figure(figsize = (10, 8), dpi = 80)
plt.scatter(result.fittedvalues, result.resid)
plt.plot([-0.3, 1.3], [0, 0], color = "black")
plt.show()

#############
import numpy as np
import pandas as pd
from sklearn.linear_model import BayesianRidge, LinearRegression, ElasticNet
from sklearn.svm import SVR
from sklearn.ensemble.gradient_boosting import GradientBoostingRegressor   # 集成算法
from sklearn.model_selection import cross_val_score    # 交叉验证
from sklearn.metrics import explained_variance_score, mean_absolute_error, mean_squared_error, r2_score  
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline

# 数据导入
df = pd.read_csv('https://raw.githubusercontent.com/ffzs/dataset/master/boston/train.csv', 
                 usecols=['lstat', 'indus', 'nox', 'rm', 'medv'])

# 可视化数据关系
sns.set(style='whitegrid', context='notebook')   #style控制默认样式,context控制着默认的画幅大小
sns.pairplot(df, size=2)
plt.savefig('x.png')
#######
# 相关度
corr = df.corr()
# 相关度热力图
sns.heatmap(corr, cmap='GnBu_r', square=True, annot=True)
plt.savefig('xx.png')

# 自变量
X = df[['lstat', 'rm']].values
# 因变量
y = df[df.columns[-1]].values

# 设置交叉验证次数
n_folds = 5

# 建立贝叶斯岭回归模型
br_model = BayesianRidge()

# 普通线性回归
lr_model = LinearRegression()

# 弹性网络回归模型
etc_model = ElasticNet()

# 支持向量机回归
svr_model = SVR()

# 梯度增强回归模型对象
gbr_model = GradientBoostingRegressor()

# 不同模型的名称列表
model_names = ['BayesianRidge', 'LinearRegression', 'ElasticNet', 'SVR', 'GBR']
# 不同回归模型
model_dic = [br_model, lr_model, etc_model, svr_model, gbr_model]
# 交叉验证结果
cv_score_list = []
# 各个回归模型预测的y值列表
pre_y_list = []

# 读出每个回归模型对象
for model in model_dic:
    # 将每个回归模型导入交叉检验
    scores = cross_val_score(model, X, y, cv=n_folds)
    # 将交叉检验结果存入结果列表
    cv_score_list.append(scores)
    # 将回归训练中得到的预测y存入列表
    pre_y_list.append(model.fit(X, y).predict(X))
### 模型效果指标评估 ###
# 获取样本量，特征数
n_sample, n_feature = X.shape
# 回归评估指标对象列表
model_metrics_name = [explained_variance_score, mean_absolute_error, mean_squared_error, r2_score]
# 回归评估指标列表
model_metrics_list = []
# 循环每个模型的预测结果
for pre_y in pre_y_list:
    # 临时结果列表
    tmp_list = []
    # 循环每个指标对象
    for mdl in model_metrics_name:
        # 计算每个回归指标结果
        tmp_score = mdl(y, pre_y)
        # 将结果存入临时列表
        tmp_list.append(tmp_score)
    # 将结果存入回归评估列表
    model_metrics_list.append(tmp_list)
df_score = pd.DataFrame(cv_score_list, index=model_names)
df_met = pd.DataFrame(model_metrics_list, index=model_names, columns=['ev', 'mae', 'mse', 'r2'])

# 各个交叉验证的结果
df_score
# 各种评估结果
df_met
### 可视化 ###
# 创建画布
plt.figure(figsize=(9, 6))
# 颜色列表
color_list = ['r', 'g', 'b', 'y', 'c']
# 循环结果画图
for i, pre_y in enumerate(pre_y_list):
    # 子网络
    plt.subplot(2, 3, i+1)
    # 画出原始值的曲线
    plt.plot(np.arange(X.shape[0]), y, color='k', label='y')
    # 画出各个模型的预测线
    plt.plot(np.arange(X.shape[0]), pre_y, color_list[i], label=model_names[i])
    plt.title(model_names[i])
    plt.legend(loc='lower left')
plt.savefig('xxx.png')
plt.show()

import pandas as pd 
import statsmodels.formula.api as smf 
import statsmodels.api as sm 

TV = [230.1, 44.5, 17.2, 151.5, 180.8] 
Radio = [37.8,39.3,45.9,41.3,10.8] 
Newspaper = [69.2,45.1,69.3,58.5,58.4] 
Sales = [22.1, 10.4, 9.3, 18.5,12.9] 
df = pd.DataFrame({'TV': TV, 
        'Radio': Radio, 
        'Newspaper': Newspaper, 
        'Sales': Sales}) 

Y = df.Sales 
X = df[['TV','Radio','Newspaper']] 
X = sm.add_constant(X) 
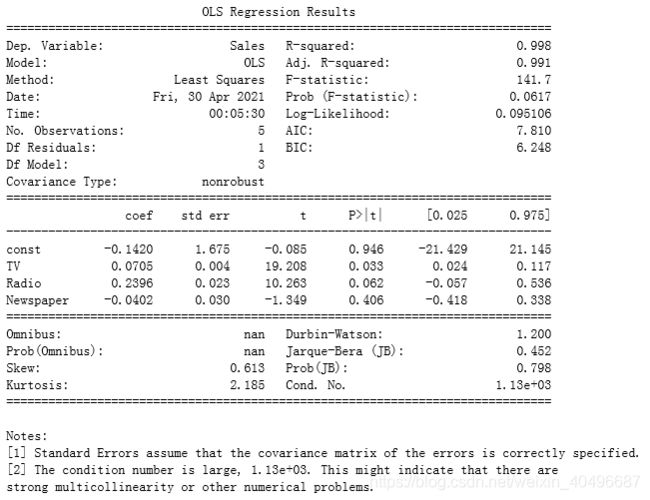
model = sm.OLS(Y, X).fit() 
print(model.summary())

我们做回归的时候，可以调用以下模块来进行：

1. 使用patsy创建模型，使用其下面的 dmatrices来生成 设计矩阵，不需要再生成常数项的1111…数列了，后面再调用statsmodels.api 来执行回归任务。
2. statsmodels的线性模型有两种不同的接口：1基于数组：import statsmodels.api as sm，需要配合 add_constant()来生成自变量矩阵。
3. statsmodels的线性模型有两种不同的接口：2基于公式：import statsmodels.formula.api as smf，写公式直接拟合方程，公式中自变量可以变为平方项、自变量相互相乘等等，很方便的。
4. 机器学习sklearn 的 linear_model模块来执行回归任务。

参考资料：python建模库介绍

同学们做最后的项目，可以参考以上博主的文章，提供了有关数据整理的系统性介绍。

伍德里奇书上的例子：

import wooldridge as woo
import numpy as np
import pandas as pd
import statsmodels.formula.api as smf

attend = woo.dataWoo('attend')
n = attend.shape[0]
# # shape[0]输出矩阵的行数, 同理shape[1]输出列数
reg = smf.ols(formula='stndfnl ~ atndrte*priGPA + ACT + I(priGPA**2) + I(ACT**2)',
              data=attend)
results = reg.fit()

# print regression table:
table = pd.DataFrame({'b': round(results.params, 4),
                      'se': round(results.bse, 4),
                      't': round(results.tvalues, 4),
                      'pval': round(results.pvalues, 4)})
print(f'table: \n{table}\n')

# estimate for partial effect at priGPA=2.59:
b = results.params
partial_effect = b['atndrte'] + 2.59 * b['atndrte:priGPA']
print(f'partial_effect: {partial_effect}\n')

# F test for partial effect at priGPA=2.59:
hypotheses = 'atndrte + 2.59 * atndrte:priGPA = 0'
ftest = results.f_test(hypotheses)
fstat = ftest.statistic[0][0]
fpval = ftest.pvalue

print(f'fstat: {fstat}\n')
print(f'fpval: {fpval}\n')

回归中的一些检验：

1. 回归系数假设检验方法（可以检验 $\beta$ 为任意值的情形）
   $$t=\frac{\hat{\beta }-E(\hat{\beta })}{S_e(\hat{\beta })}\sim t(n-k-1)$$
   其中：

注意： $x=X_i-\bar{X}$

$$S_e(\hat{\beta })=\frac{\hat{\sigma }}{\sqrt{\sum x_i^2}},\hat{\sigma }扰动项方差，算法是：$$

$${\hat{\sigma }}^2=\frac{\sum e_i^2}{n-k-1}$$

比如： $H0$ ： $\beta$=8 等等，其实就是把8带入到 $E(\hat{\beta })$ 的位置，然后去计算 T 值。

2. 系数的显著性检验：即 $\beta$=0 的检验
   $$t=\frac{\hat{\beta }-0}{S_e(\hat{\beta })}\sim t(n-k-1)$$

3. 全部斜率系数 $\beta$ 为 0 的 $F$ 检验。
   $$F=\frac{{\sum }_{i=1}^N(\widehat{Y_i}-\overline{Y_i}{)}^2/k}{{\sum }_{i=1}^N(Y_i-\widehat{Y_i}{)}^2/(n-k-1)}$$

教材的公式有误。

$$公式变形后有：F=\frac{n-k-1}{k}\ast \frac{R^2}{1-R^2}$$
所以，F 检验和 拟合优度 是有联系的。

5. 方程拟合优度 $R^2$
   $$R^2=\frac{解释的变差}{总变差}=\frac{ESS}{TSS}$$

$$\frac{ESS}{TSS}=\frac{{\sum }_{i=1}^N(\widehat{Y_i}-\bar{Y}{)}^2}{{\sum }_{i=1}^N(Y_i-\bar{Y}{)}^2}=1-\frac{{\sum }_{i=1}^N{e}_i^2}{{\sum }_{i=1}^N(Y_i-\bar{Y}{)}^2}$$

判断拟合效果的统计量还有：平均绝对误差MAE 和 均方根误差 RMSE。

$$MAE=\frac{{\sum }_{i=1}^N\left|\widehat{Y_i}-Y_i\right|}{N}$$

$$RMSE=\sqrt{\frac{{\sum }_{i=1}^N(\widehat{Y_i}-Y_i{)}^2}{N}}$$

6. 双变量回归中 $Y$的置信区间（其中：$x=X_i-\bar{X}$

$$\frac{Y_0-\widehat{Y_0}}{\hat{\sigma }\ast \sqrt{1+\frac{1}{n}+\frac{(X_0-\bar{X}{)}^2}{\sum x^2}}}\sim t(n-2)$$

则$\widehat{Y_0}$ 的 95% 置信区间为：
$$(\hat{\alpha }+\hat{\beta }{X}_0)\pm t_{0.025}(n-2)\ast \hat{\sigma }\ast \sqrt{1+\frac{1}{n}+\frac{(X_0-\bar{X}{)}^2}{\sum x^2}}$$

import pandas as pd 
import statsmodels.formula.api as smf 
import statsmodels.api as sm 

TV = [230.1, 44.5, 17.2, 151.5, 180.8] 
Radio = [37.8,39.3,45.9,41.3,10.8] 
Newspaper = [69.2,45.1,69.3,58.5,58.4] 
Sales = [22.1, 10.4, 9.3, 18.5,12.9] 
df = pd.DataFrame({'TV': TV, 
        'Radio': Radio, 
        'Newspaper': Newspaper, 
        'Sales': Sales}) 

Y = df.Sales 
X = df[['TV','Radio','Newspaper']] 
X = sm.add_constant(X) 
model = sm.OLS(Y, X).fit() 
print(model.summary())

1.提取元素-回归系数类

# 提取回归系数
model.params

# 提取回归系数标准差
model.bse

# 提取回归系数p值
model.pvalues

# 提取回归系数t值
model.tvalues

# 提取回归系数置信区间 默认5%，括号中可填具体数字 比如0.05, 0.1
model.conf_int()  

# 提取模型预测值
model.fittedvalues

# 提取残差
model.resid

# 模型自由度（系数自由度）
model.df_model

# 残差自由度（样本自由度）
model.df_resid

# 模型样本数量
model.nobs

2.模型评价类:

# 提取R方
model.rsquared

# 提取调整R方
model.rsquared_adj

# 提取AIC
model.aic

# 提取BIC
model.bic

# 提取F-statistic
model.fvalue

# 提取F-statistic 的pvalue
model.f_pvalue

# 模型mse
model.mse_model

# 残差mse
model.mse_resid

# 总体mse
model.mse_total

3.下面是不太常用的计量经济学方面的系数:

# 协方差矩阵比例因子
model.scale

#  White异方差稳健标准误
model.HC0_se

# MacKinnon和White（1985）的异方差稳健标准误
model.HC1_se

#  White异方差矩阵
model.cov_HC0

# MacKinnon和White（1985）的异方差矩阵
model.cov_HC1

以上可查阅这篇文章

参考文章：

Python实现多元线性回归

Python实现多元线性回归

Python 实战多元线性回归模型

Python 实现多元线性回归预测

利用scipy, seaborn 做假设检验，回归分析