pytorch geometric教程四 利用NeighorSampler实现节点维度的mini-batch + GraphSAGE样例

PyG的官方文档中有mini-batch和Advanced mini-batching两部分内容，但实现的都是图维度的mini-batch。如何像GraphSAGE paper中对minibatch的节点进行邻居采样并训练模型，使得大规模全连接图的GNNs模型训练成为可能，PyG是通过torch_geometric.loader.NeighborSampler实现的（早一点版本是torch_geometric.data.NeighborSampler）。
需要注明的一点是，这篇文章中虽然举了SAGEConv的代码样例，但只要卷积层支持bipartite图，大家举一反三，就可以与NeighborSampler结合使用，实现节点维度的mini-batch模型训练与推断。

class NeighborSampler

核心想法

NeighborSampler的核心想法是，给定mini-batch的节点和图卷积的层数L，以及每一层需要采样的邻居数目sizes，依次从第一层到第L层，对每一层进行邻居采样并返回一个bipartite子图。sizes是一个L长度的list，包含每一层需要采样的邻居个数。以下是主要逻辑的归纳：

For i in L:

• 第1层使用初始minibatch的节点进行邻居采样，返回采样结果。
• 第i (i>0)层，使用上层采样中涉及到的所有节点进行邻居采样，返回采样结果。

L层采样完成后，返回结果(batch_size, n_id, adjs)，其中batch_size就是mini-batch的节点数目，n_id是包含所有在L层卷积中遇到的节点的list，且target节点在n_id前几位。adjs是一个list，包含了从第L层到第1层采样的结果，所以adjs中的子图是从大到小的。每一层采样返回的结果具体形式为 (edge_index, e_id, size)。其中edge_index是采样得到的bipartite子图中source节点到target节点的边。e_id是edge_index的边在原始大图中的IDs，size就是bipartite子图的shape。

以下是一个2层采样的示意图，注意在第2层采样的时候，使用了第1层中涉及到的所有节点，包括出发点。

返回结果

整理一下， NeighborSampler的返回结果如下：

• batch_size
• n_id：L层采样中遇到的所有的节点的list，其中target节点在list最前端
• adjs：第L层到第1层采样结果的list
  • edge_index：采样得到的bipartite子图中source节点到target节点的边
  • e_id：edge_index的边在原始大图中的IDs
  • size：bipartite子图的shape

参数

class NeighborSampler(torch.utils.data.DataLoader):
    def __init__(self, edge_index: Union[Tensor, SparseTensor],
                 sizes: List[int], node_idx: Optional[Tensor] = None,
                 num_nodes: Optional[int] = None, return_e_id: bool = True,
                 transform: Callable = None, **kwargs):

• edge_index (Tensor or SparseTensor)：图的边信息，可以是Tensor，也可以是SparseTensor。
• sizes ([int])：每一层需要采样的邻居数目，如果是-1的话，选取所有的邻居。
• node_idx (LongTensor, optional)：提供需要被采样节点的信息，比如模型训练的时候，只给出数据集train中的节点。在预测的时候，使用None，考虑所有的节点。
• num_nodes: Optional[int] = None：图中节点的数目，可选参数。
• return_e_id: bool = True：当设为False的时候，不会返回partite子图的边在原图中的IDs。
• transform
• **kwargs：NeighborSampler是torch.utils.data.DataLoader的子类，所以父类DataLoader的参数NeighborSampler都可以使用，比如:batch_size, shuffle, num_workers。

NeighborSampler在GraphSAGE代码中的使用

先看一下NeighborSampler如何和卷积一起使用，后面再看它具体是如何工作的。
PyG关于GraphSAGE给了两个代码样例reddit和ogbn_prodcuts_sage，下面具体解释一下reddit代码中NeighborSampler的相关部分，我删掉了一些不太重要的代码内容。

模型训练

train_loader

首先代码里定义了模型训练时的数据加载器train_loader。 node_idx=data.train_mask指定只对训练集的节点进行邻居采样，sizes=[25, 10]指明了这是一个两层的卷积，第一层卷积采样邻居数目25，第二层卷积采样邻居数目10。batch_size=1024指定了mini-batch的节点数目，每次只对1024个节点进行采样。

train_loader = NeighborSampler(data.edge_index, node_idx=data.train_mask,
                               sizes=[25, 10], batch_size=1024, shuffle=True,
                               num_workers=12)

train

train_loader每次返回一个batch_size节点邻居采样的结果，其形式是(batch_size, n_id, adjs)，其中n_id是采样过程中涉及的所有节点的id，也是adjs中涉及的所有节点，因此x[n_id]是所有相关节点的特征。而且x[n_id]相当于做了一次映射，x[n_id]中第i行就是adjs中i节点的特征（关于这一点，会在后面NeighborSampler工作原理部分详述）。adjs是包含了所有bipartite子图边信息的list。所以model(x[n_id], adjs)传入了所有bipartite子图的节点特征和边信息。
另外NeighborSampler是在CPU中完成的，所以返回的结果都在CPU上。如果用GPU训练模型，要记得将loader的结果放到GPU上。

def train(epoch):
    model.train()
    
    total_loss = total_correct = 0
    for batch_size, n_id, adjs in train_loader:
        # `adjs` holds a list of `(edge_index, e_id, size)` tuples.
        adjs = [adj.to(device) for adj in adjs]

        optimizer.zero_grad()
        out = model(x[n_id], adjs)
        loss = F.nll_loss(out, y[n_id[:batch_size]])
        loss.backward()
        optimizer.step()

        total_loss += float(loss)
        total_correct += int(out.argmax(dim=-1).eq(y[n_id[:batch_size]]).sum())

    loss = total_loss / len(train_loader)
    approx_acc = total_correct / int(data.train_mask.sum())
    
    return loss, approx_acc

model中的forward()函数

forward函数依次实现了从第L层到第1层采样得到的bipartite子图的卷积。
adjs包含L层邻居采样的bipartite子图：(edge_index, e_id, size)。在上一个教程中讲过了，SAGEConv是支持bipartite图的。对bipartite图进行卷积时，输入的x是一个tuple: (x_source, x_target)。上面提到过，n_id是包含所有在L层卷积中遇到的节点的list，且target节点在n_id前几位。而bipartite图的size是(num_of_source_nodes, num_of_target_nodes)，因此对每一层的bipartite图都有x_target = x[:size[1]] 。所以 self.convs[i]((x, x_target), edge_index)实现了对一层bipartite图的卷积。

class SAGE(torch.nn.Module):
    def __init__(self, in_channels, hidden_channels, out_channels, num_layers):
        super(SAGE, self).__init__()
        self.num_layers = num_layers
        ...

    def forward(self, x, adjs):
        for i, (edge_index, _, size) in enumerate(adjs):
            x_target = x[:size[1]]  # Target nodes are always placed first.
            x = self.convs[i]((x, x_target), edge_index)
            if i != self.num_layers - 1:
                x = F.relu(x)
                x = F.dropout(x, p=0.5, training=self.training)
        return x.log_softmax(dim=-1)

模型推断：

subgraph_loader, inference函数和test()

做推断时，不再对邻居进行采样，而是取所有的邻居，因此subgraph_loader中的sizes设成了[-1]，取所有的一阶邻居。但是这里的SAGE模型是一个两层的卷积层，为什么不取所有的二阶邻居，将sizes设成了[-1, -1]呢？我们看一下这个代码样例中的inference函数。

subgraph_loader = NeighborSampler(data.edge_index, node_idx=None, sizes=[-1],
                                  batch_size=1024, shuffle=False,
                                  num_workers=12)

class SAGE(torch.nn.Module):
    def __init__(self, in_channels, hidden_channels, out_channels, num_layers):
        super(SAGE, self).__init__()
        self.num_layers = num_layers
		...

    def inference(self, x_all):
        for i in range(self.num_layers):
            xs = []
            for batch_size, n_id, adj in subgraph_loader:
                edge_index, _, size = adj.to(device)
                x = x_all[n_id].to(device)  #使用上一层卷积跟新过的embedding, x_all
                x_target = x[:size[1]]
                x = self.convs[i]((x, x_target), edge_index)
                if i != self.num_layers - 1:
                    x = F.relu(x)
                xs.append(x.cpu())

            x_all = torch.cat(xs, dim=0)   # 使用这一层卷积得到的embedding来更新x_all
        return x_all

注意到其中有一个for i in range(self.num_layers)的循环，总结inference在做的事情就是：

for i in L:
	对于所有节点，利用一阶邻居更新embedding

不是取所有的n阶邻居，计算一次就得到节点最终的embedding，这里用的技巧是，只取所有一阶邻居，但是迭代跟新n次。这两种方式的结果是相同的。

但是为什么要使用这种曲折的方式，而不是直接取n阶邻居呢？

首先训练的时候为什么要对邻居采样，就是因为整张图的计算非常消耗内存。所以设计了minibatch邻居采样的计算方式，同时实现了更快收敛和内存节省。而推断如果取全部n阶邻居，随着邻居节点数的指数级增多，也会使内存消耗指数级增加。对于比较稠密的图，或者图中存在度数很大的节点的时候，n阶邻居可能相当于把整张图放了进来，或许会出现out of memory的情况。 所以只取一阶邻居，但是迭代n次，是计算效率更高，内存消耗更小的方法。尤其对于比较稠密的图，这一点体现更为明显。

NeighborSampler工作原理&具体实例

上文只是简略讲了NeighborSampler的工作原理，这里用几个实例，让大家更清楚地理解其中的细节。
首先用networkx建以下一张图:

import networkx as nx
graph = nx.Graph()
graph.add_edges_from([(0,1), (1,2), (1,3), (2,3), (3,4), (4,2)])
nx.draw_kamada_kawai(graph, with_labels=True)

将其转换成PyG中的Data格式。

from torch_geometric.data.data import Data
from torch_geometric.utils import from_networkx

data = from_networkx(graph)
data.edge_index
>>> tensor([[0, 1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4],
        [1, 0, 2, 3, 1, 3, 4, 1, 2, 4, 2, 3]])

batch_size =1 ，采样邻居数小于邻居数

from torch_geometric.data import NeighborSampler
loader = NeighborSampler(edge_index=data.edge_index, sizes=[2], node_idx=torch.tensor([2]), batch_size=1)
next(iter(loader))
>>> (1,
 tensor([2, 3, 1]),
 EdgeIndex(edge_index=tensor([[1, 2],
         [0, 0]]), e_id=tensor([8, 2]), size=(3, 1)))

以上代码对2号节点取两个邻居。n_id: tensor([2, 3, 1])是遇到的所有节点，target节点在最前面，是2号节点，3, 1是采样到的邻居。edge_index=tensor([[1, 2], [0, 0]])是采样得到的bipartite子图。n_id中的index对应edge_index中的数值。edge_index[1]中是target节点，bipartite子图是从target节点开始计数的，所以n_id里面永远是target节点在前几位。另外size[0]是source节点的数目，size[1]是target节点的数目，所以n_id[size[1]]可以获取target节点在原图中的id。看以下示意图：

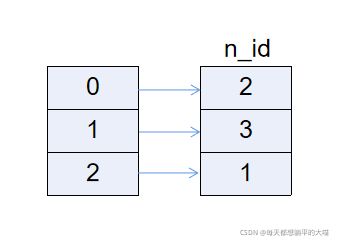
知道了bipartite子图中的节点对应原图哪个节点后，还可以将bipartite子图中的边对应到原图中的边。看以下示意图：

边[3,2]和边[1,2]分别是原图中的第8，第2条边，和返回的e_id相同。

batch_size =1 ，采样邻居数大于邻居数

以下结果可以看出，当采样邻居数大于邻居数的时候，NeighborSampler不会对邻居进行随机填充。这是因为在源码中，作者将采样的replace设置成了False。

from torch_geometric.data import NeighborSampler
loader = NeighborSampler(edge_index=data.edge_index, sizes=[4], node_idx=torch.tensor([2]), batch_size=1)
next(iter(loader))
>>>(1,
 tensor([2, 4, 1, 3]),
 EdgeIndex(edge_index=tensor([[1, 2, 3],
         [0, 0, 0]]), e_id=tensor([10,  2,  8]), size=(4, 1)))

batch_size = [2, 2]

from torch_geometric.data import NeighborSampler
loader = NeighborSampler(edge_index=data.edge_index, sizes=[2, 2], node_idx=torch.tensor([2]), batch_size=1)
next(iter(loader))
>>> (1,
 tensor([2, 4, 1, 3, 0]),
 [EdgeIndex(edge_index=tensor([[2, 3, 0, 3, 0, 4],
          [0, 0, 1, 1, 2, 2]]), e_id=tensor([2, 8, 6, 9, 4, 0]), size=(5, 3)),
  EdgeIndex(edge_index=tensor([[1, 2],
          [0, 0]]), e_id=tensor([10,  2]), size=(3, 1))])

其中EdgeIndex(edge_index=tensor([[1, 2], [0, 0]]), e_id=tensor([10, 2]), size=(3, 1))是第一层采样得到的bipartite图， EdgeIndex(edge_index=tensor([[2, 3, 0, 3, 0, 4], [0, 0, 1, 1, 2, 2]]), e_id=tensor([2, 8, 6, 9, 4, 0]), size=(5, 3))是第二层采样得到的bipartite图。
可以看出来，第二层采样是建立在第一层采样的基础上的，第一层采样bipartite中所有的节点[0, 1, 2] （在原图中对应[2, 4, 1]）作为第二层采样的出发点。所以edge_index[1]有[0, 0, 1, 1, 2, 2]，这是将0, 1, 2作为target节点采样两个邻居的结果。

就不再赘述更多样例了，大家可以自己试一试，玩一玩。

欢迎多交流，转发请注明出处。

实战代码

https://github.com/DGraphXinye/2022_finvcup_baseline
这是我为我们公司比赛准备的baseline代码，里面包含了基本的图算法以及相应的mini-batch版本。