R语言:感知机模型(二)
Hello,大家好!今天给大家分享的是感知机模型的对偶形式,这篇发完后第二章感知机就结束了,后续会直接跳到第七章支持向量机;另外理论推导和证明大家直接看书(文末可获得电子书),就不再抄一遍了,只写算法思路和代码实现。
目录
-
- 算法:感知机学习算法的对偶形式
- R语言代码
-
- 效果展示
- 相关文章
- 资源获取
算法:感知机学习算法的对偶形式
李航《统计学习方法》(第2版)P44——算法2.2
输入:线性可分的数据集 T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x N , y N ) } T=\{(x_1,y_1),(x_2,y_2),\dots,(x_N,y_N)\} T={(x1,y1),(x2,y2),…,(xN,yN)},其中 x i ∈ R n , y i ∈ { − 1 , + 1 } , i = 1 , 2 , … , N x_i\in \mathbf{R}^n,y_i\in \{-1,+1\},i=1,2,\dots,N xi∈Rn,yi∈{−1,+1},i=1,2,…,N;学习率 η ( 0 < η ⩽ 1 ) \eta(0<\eta\leqslant 1) η(0<η⩽1);
输出: α , b \alpha,b α,b;感知机模型 f ( x ) = s i g n ( ∑ j = 1 N α j y j x j ∙ x + b ) f(x)=\mathrm{sign}(\sum_{j=1}^N \alpha_jy_jx_j\bullet x+b) f(x)=sign(∑j=1Nαjyjxj∙x+b),其中 α = ( α 1 , α 2 , … , α N ) T \alpha =(\alpha_1,\alpha_2,\dots,\alpha_N)^T α=(α1,α2,…,αN)T。
(1) α ← 0 , b ← 0 \alpha\leftarrow0,b\leftarrow0 α←0,b←0;
(2)在训练集中选取数据 ( x i , y i ) (x_i,y_i) (xi,yi);
(3)如果 y i ( ∑ j = 1 N α j y j x j ∙ x i + b ) ⩽ 0 y_i(\sum_{j=1}^N\alpha_jy_jx_j\bullet x_i+b)\leqslant0 yi(∑j=1Nαjyjxj∙xi+b)⩽0,
KaTeX parse error: No such environment: align* at position 8: \begin{̲a̲l̲i̲g̲n̲*̲}̲ \alpha_i & \le…
(4)转至(2)直到没有误分类数据
对偶形式中训练实例仅以内积的形式出现。可预先以矩阵的形式储存,即Gram矩阵
G = [ x i , x j ] N × N G=[x_i,x_j]_{N\times N} G=[xi,xj]N×N
R语言代码
上一篇是直接用了李航书里的习题案例,这次随机生成20个数据来玩玩:
x1<-runif(20,0,10)
x2<-runif(20,0,10)
y<-sign(1.7*x1-3.1*x2+1.2)
data <- data.frame(y=y,x1=x1,x2=x2)
注:图中虚线是真实分离超平面,用于后续参照。
(1)设置初值 α 0 , b 0 \alpha_0,b_0 α0,b0;学习率 η \eta η;最大迭代次数;Gram矩阵;
y<-as.matrix(data[,1])
x<-as.matrix(data[,-1])
eta<-0.5
max_iter<-100
alpha<-matrix(0,nrow(data),1)
b<-0
G<-x%*%t(x)
(2)循环判断 y i ( ∑ j = 1 N α j y j x j ∙ x i + b ) y_i(\sum_{j=1}^N\alpha_jy_jx_j\bullet x_i+b) yi(∑j=1Nαjyjxj∙xi+b)的结果中是否有 ⩽ 0 \leqslant0 ⩽0的样本;如果有,则更新 α , b \alpha,b α,b;
out<-FALSE
for (k in 1:max_iter) {
for (i in 1:nrow(data)) {
if (y[i]*(sum(alpha*y*G[i,])+b)<=0){
alpha[i]<-alpha[i]+eta
b<-b+eta*y[i]
break()
}
if (y[i]*(sum(alpha*y*G[i,])+b)>0 & i==nrow(data)){
out<-TRUE
print(paste(c("w1:","w2:"),c(sum(alpha*y*x[,1]),sum(alpha*y*x[,2]))))
print(paste("b:",b))
}
}
if (out){break}
}
注:
上篇文章里面直接用矩阵运算代替了循环,这次完全按照算法,循环判断,可以明显看出样本量如果越大,运算效率是非常低下的;所以封装的时候还是用矩阵运算来代替,具体见完整代码
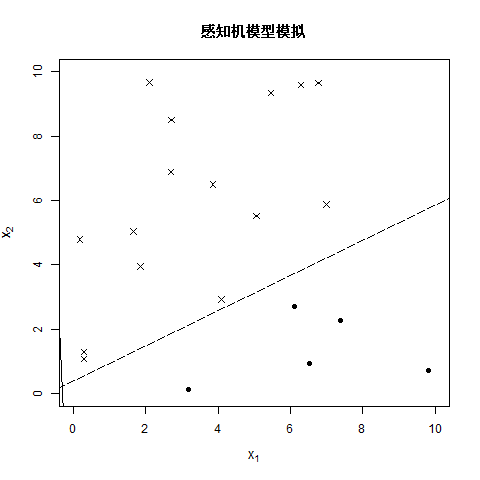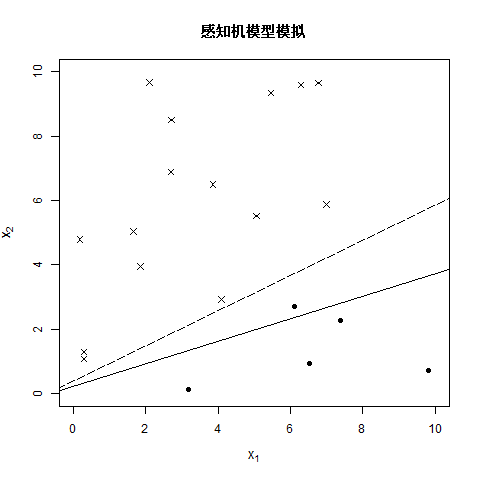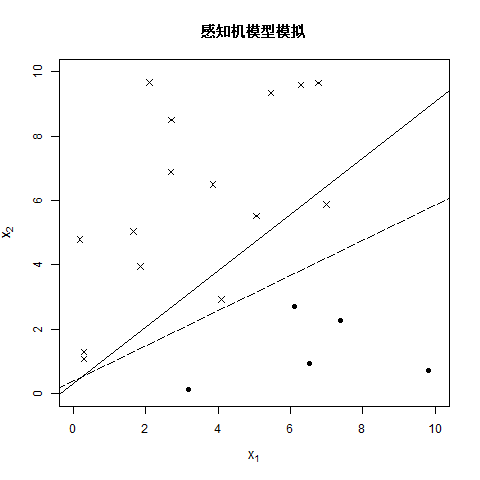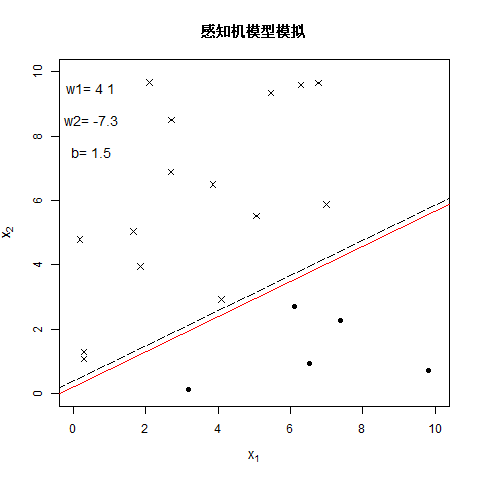
效果展示
老样子制作了一个动图,来观看每次的迭代效果,最终得到的结果为 w 1 = 4.1 , w 2 = − 7.3 , b = 1.5 w_1=4.1,w_2=-7.3,b=1.5 w1=4.1,w2=−7.3,b=1.5,成功分离了所有的样本点。
相关文章
- 李航《统计学习导论》第二章 感知机:R语言:感知机模型(一)
资源获取
- 关注公众号,回复“《统计学习方法》”,获得电子书;
- 关注公众号,回复“感知机二”,获得本文完整代码。