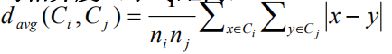聚类

目录

目录

聚类

聚类分析概述

1.聚类分析的定义

2.聚类分析在数据挖掘中的作用：

3.常用的聚类分析方法：

相似性计算方法

连续型属性的相似性计算方法

二值离散型属性的相似性计算方法

多值离散型属性的相似性计算方法

混合类型属性的相似性计算方法

k-means算法

k-medoids算法

AGNES (Agglomerative Nesting)算法(合并聚类)

DIANA (Divisive Analysis)算法（分类聚类法）

DBSCAN

sklearn

sklearn-dbscan

sklearn_k-means

sklearn_minibatchk-means

---

---

聚类

聚类分析概述

简单地描述，聚类(Clustering)是将数据集划分为若干相似对象组成的多个组(group)或簇(cluster)的过程，使得同一组中对象间的相似度最大化，不同组中对象间的相似度最小化。或者说一个簇(cluster)就是由彼此相似的一组对象所构成的集合，不同簇中的对象通常不相似或相似度很低。

1.聚类分析的定义

– 聚类分析(Cluster Analysis)是一个将数据集中的所 有 数 据 ， 按 照 相 似 性 划 分 为 多 个 类 别
（Cluster, 簇）的过程；
     • 簇是相似数据的集合。
– 聚类分析是一种无监督(Unsupervised Learning)分类方法：数据集中的数据没有预定义的类别标号（无训练集和训练的过程）。
– 要求：聚类分析之后，应尽可能保证类别相同的数据之间具有较高的相似性，而类别不同的数据之间具有较低的相似性

2.聚类分析在数据挖掘中的作用：

– 作为一个独立的工具来获得数据集中数据的分布情况；
    • 首先，对数据集执行聚类，获得所有簇；
    • 然后，根据每个簇中样本的数目获得数据集中每类数据的大体分布情况。
– 作为其他数据挖掘算法的预处理步骤。
   • 首先，对数据进行聚类——粗分类；
   • 然后，分别对每个簇进行特征提取和细分类，可以有效提高分类精度

3.常用的聚类分析方法：

– 划分法（Partitioning Methods）：以距离作为数据集中不同数据间的相似性度量，将数据集划分成多个簇。

– 划分准则：同一个簇中的样本尽可能接近或相似，不同簇中的样本尽可能远离或不相似。
– 以样本间的距离作为相似性度量
      • 属于这样的聚类方法有：k-means（k-均值算法）由簇中样本的平均值来代表整个簇、k-medoids（k-中心算法）由处于簇中心区域的某个样本代表整个簇等。
– 层次法（Hierarchical Methods）：对给定的数据集进行层次分解，形成一个树形的聚类结果。
      • 属于这样的聚类方法有：

          自顶向下法（合并）：开始时，将每个样本作为单独的一个组；然后，依次合并相近的样本或组，直至所有样本或组被合                                                并为一个组或者达到终止条件为止。代表算法：AGNES算法（合并聚类法）

          自底向上法（分裂）：开始时，将所有样本置于一个簇中；然后，执行迭代，在迭代的每一步中，一个簇被分裂为多个更                                               小的簇，直至每个样本分别在一个单独的簇中或者达到终止条件为止。代表算法：DIANA算法（分                                               裂聚类法）。
– 密度法

      • 基于密度的聚类： DBSCAN算法

相似性计算方法

在聚类分析中，样本之间的相似性通常采用样本之间的距离来表示。
– 两个样本之间的距离越大，表示两个样本越不相似性，差异性越大；
– 两个样本之间的距离越小，表示两个样本越相似性，差异性越小。
– 特例：当两个样本之间的距离为零时，表示两个样本完全一样，无差异。

– 样本之间的距离是在样本的描述属性（特征）上进行计算的。
– 在不同应用领域，样本的描述属性的类型可能不同，因此相似性的计算方法也不尽相同。
• 连续型属性(如：重量、高度、年龄等)
• 二值离散型属性(如：性别、考试是否通过等)
• 多值离散型属性(如：收入分为高、中、低等)
• 混合类型属性(上述类型的属性至少同时存在两种)

连续型属性的相似性计算方法

• 假设两个样本Xi和Xj分别表示成如下形式：

             
           – 它们都是d维的特征向量，并且每维特征都是一个连续型数值。
• 对于连续型属性，样本之间的相似性通常采用如下三种距离公式进行计算。

二值离散型属性的相似性计算方法

•二值离散型属性只有0和1两个取值。
    – 其中：0表示该属性为空，1表示该属性存在。
    – 例如：描述病人的是否抽烟的属性(smoker)，取值为1表示病人抽烟，取值0表示病人不抽烟。
• 假设两个样本Xi和Xj分别表示成如下形式：

                
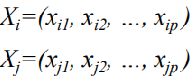
    – 它们都是p维的特征向量，并且每维特征都是一个二值离散型数值

• 假设二值离散型属性的两个取值具有相同的权重，则可以得到一个两行两列的可能性矩阵

• 如果样本的属性都是对称的二值离散型属性，则样本间的距离可用简单匹配系数(Simple Matching Coefficients, SMC)计算：
SMC = (b + c) / (a + b + c + d)

    – 其中：对称的二值离散型属性是指属性取值为1或者0同等重要。
    – 例如：性别就是一个对称的二值离散型属性，即：用1表示男性，用0表示女性；或者用0表示男性，用1表示女性是等价的，属性的两个取值没有主次之分

•如果样本的属性都是不对称的二值离散型属性，则样本间的距离可用Jaccard系数计算(Jaccard Coefficients, JC)：
JC = (b + c) / (a + b + c)

– 其中：不对称的二值离散型属性是指属性取值为1或者0不是同等重要。
– 例如：血液的检查结果是不对称的二值离散型属性，阳性结果的重要程度高于阴性结果，因此通常用1来表示阳性结果，而用0来表示阴性结果。

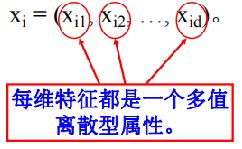
多值离散型属性的相似性计算方法

• 多值离散型属性是指取值个数大于2的离散型属性。
     – 例如：成绩可以分为优、良、中、差。
• 假设一个多值离散型属性的取值个数为N，给定数据集X={xi | i=1,2,…,total}。
     – 其中：每个样本xi可用一个d维特征向量描述，并且每维特征都是一个多值离散型属性，即：

– 方法一：简单匹配方法。
       • 距离计算公式如下：

        
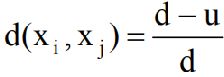
      • 其中： d为数据集中的属性个数，u为样本xi和xj取值相同的属性个数

– 方法二：先将多值离散型属性转换成多个二值离散型属性，然后再使用Jaccard系数计算样本之间的距离。
      • 对有N个取值的多值离散型属性，可依据该属性的每种取值分别创建一个新的二值离散型属性，这样可将多值离散型属性转换成多个二值离散型属性

混合类型属性的相似性计算方法

方法：将混合类型属性放在一起处理，进行一次聚类分析。
– 在聚类之前，对样本的属性值进行预处理：
   • 对连续型属性，将其各种取值进行规范化处理，使得属性值规范化到区间[0.0, 1.0]；
   • 对多值离散型属性，根据属性的每种取值将其转换成多个二值离散型属性。
   • 预处理之后，样本中只包含连续型属性和二值离散型属性。

k-means算法

算法思想
    初始随机给定K个簇中心，按照最邻近原则把待分类样本点分到各个簇。然后按平均法重新计算各个簇的质心，从而确定新的簇心。一直迭代，直到簇心的移动距离小于某个给定的值

import numpy as np
a = np.array([(3,4),(3,6),(7,3),(4,7),(3,8),(8,5),(4,5),(4,1),(7,4),(5,5)])
lines = ""
for i in a:
    for j in a:
        dis = np.sqrt(np.sum((i-j)**2))
        lines+="%.2f"%dis+","
    lines+="\n"
file = open("result.csv",mode="w",encoding="utf-8")
file.write(lines)
file.close()

"""
1.随机取k个中心点
2. 计算所有点到中心点的距离
    将所有点 分别放入 中心点所在的簇
        更新中心点
            如果中心点不变 结束迭代
    迭代
"""
import numpy as np
import matplotlib.pyplot as plt

#获取数据集
def loadDataSet(filename):
    return np.loadtxt(filename,delimiter=",",dtype=np.float)

#取出k个中心点
def initCenters(dataset,k):
    """
    返回的k个中心点
    :param dataset:数据集
    :param k:中心点的个数
    :return:
    """
    centersIndex =  np.random.choice(len(dataset),k,replace=False)
    return dataset[centersIndex]
#计算距离公式
def distance(x,y):
    return np.sqrt(np.sum((x-y)**2))

#kmeans的核心算法
def kmeans(dataset,k):
    """
    返回k个簇
    :param dataset:
    :param k:
    :return:
    """
    #初始化中心点
    centers = initCenters(dataset,k)
    n,m = dataset.shape
    #用于存储每个样本属于哪个簇
    clusters = np.full(n,np.nan)
    #迭代 标志
    flag = True
    while flag:
        flag = False
        #计算所有点到簇中心的距离
        for i in range(n):
            minDist,clustersIndex = 99999999,0
            for j in range(len(centers)):
                dist = distance(dataset[i],centers[j])
                if dist2:
        print("维度大于2")
        return 1
    #根据簇不同 marker不同
    colors = ["r","g","b","y"]
    for i in range(n):
        clusterIndex = clusters[i].astype(np.int)
        plt.plot(dataset[i][0],dataset[i][1],color=colors[clusterIndex],marker="o")
    for i in range(k):
        plt.scatter(centers[i][0],centers[i][1],marker="s")
    plt.show()
if __name__=="__main__":
    dataset = loadDataSet("testSet.txt")
    clusters,centers = kmeans(dataset,4)
    show(dataset,4,clusters,centers)

p是蔟Ci中的样本

mi是蔟Ci的均值

k是蔟的个数

• 优点：
     – 可扩展性较好，算法复杂度为O(nkt)。
          • 其中：n为样本个数，k是簇的个数，t是迭代次数。
• 缺点：
     – 簇数目k需要事先给定，但非常难以选定；
     – 初始聚类中心的选择对聚类结果有较大的影响；
     – 不适合于发现非球状簇；
     – 对噪声和离群点数据敏感

k-medoids算法

k-medoids算法基本思想：
– 选取有代表性的样本（而不是均值）来表示整个簇，即：选取最靠近中心点(medoid)的那个样本来代表整个簇。
– 以降低聚类算法对离群点的敏感度。
– PAM (Partitioning Around Medoids, 围绕中心点的划分)算法，于1987年提出

如果代表样本能被非代表样本所替代，则替代产生的总代价S是所有样本产生的代价之和。
n总代价的定义如下：

• 当非代表样本Orandom替代代表样本Oj后，对于数据集中的每一个样本p，它所属的簇的类别将有以下四种可能的变化：

 

k-medoids与k-means的比较
• 当存在噪声和离群点时，k-medoids算法比k-means算法更加鲁棒(稳定)。
 – 这是因为中心点不像均值那样易被极端数据(噪声或者离群点)影响。
• k-medoids算法的执行代价比k-means算法要高。
  – k-means算法： O(nkt)

  – k-medoids算法：O(k(n-k)^2)
• 当n与k较大时， k-medoids算法的执行代价很高。
• 两种方法都需要事先指定簇的数目k。

AGNES (Agglomerative Nesting)算法(合并聚类)

– 首先，将数据集中的每个样本作为一个簇；
– 然后，根据某些准则将这些簇逐步合并；
– 合并的过程反复进行，直至不能再合并或者达到结束条件为止。
• 合并准则：每次找到距离最近的两个簇进行合并。
– 两个簇之间的距离由这两个簇中距离最近的样本点之间的距离来表示

AGNES算法（自底向上合并算法）
输入：包含n个样本的数据集，终止条件簇的数目k。
输出：k个簇，达到终止条件规定的簇的数目。
(1) 初始时，将每个样本当成一个簇；
(2) REPEAT  根据不同簇中最近样本间的距离找到最近的两个簇；合并这两个簇，生成新的簇的集合；
(3) UNTIL 达到定义的簇的数目

在这个算法中，需要使用单链接(Single- Link)方法和相异度矩阵。
– 单链接方法用于确定任意两个簇之间的距离；

– 相异度矩阵用于记录任意两个簇之间的距离（它是一个下三角矩阵，即：主对角线及其上方元素全部为零）

AGNES算法的优、缺点：
– 算法简单，但有可能遇到合并点选择困难的情况；
– 一旦不同的簇被合并，就不能被撤销；
–  算法的时间复杂度为O(n^2)
–  因此不适用处理n很大的数据集

DIANA (Divisive Analysis)算法（分类聚类法）

– 在该种层次聚类算法中，也是以希望得到的簇的数目作为聚类的结束条件。
– 同时，使用下面两种测度方法：
• 簇的直径：在一个簇中，任意两个样本间距离的最大值。
• 平均相异度（平均距离）

DIANA算法（自顶向下分裂算法）
输入：包含n个样本的数据集，终止条件簇的数目k。
输出：k个簇，达到终止条件规定的簇的数目。
（1）初始时，将所有样本当成一个簇；
（2） FOR （i=1; i≠k; i++) DO BEGIN
（3） 在所有簇中挑出具有最大直径的簇C；
（4） 找出C中与其它点平均相异度最大的一个点p，并把p放入splinter group，剩余的放在old party中；
（5） REPEAT
（6） 在old party里找出到最近的splinter group中的点的距离不大于到old party中最近点的距离的点，并将该点加入splinter                  group。
（7） UNTIL 没有新的old party的点被分配给splinter group；
（8） splinter group和old party为被选中的簇分裂成的两个簇，与其它簇一起组成新的簇集合。
（9） END

DBSCAN

• DBSCAN是一个基于密度的聚类算法.(他聚类方法大都是基于对象之间的距离进行聚类，聚类结果是球状的簇)
• 基于密度的聚类是寻找被低密度区域分离的高密度区域。

传统基于中心的密度定义为：
– 数据集中特定点的密度通过该点Eps半径之内的点计数(包括本身)来估计。
– 显然，密度依赖于半径。

基于密度定义，我们将点分为：
– 稠密区域内部的点(核心点) :在半径Eps内含有超过MinPts数目的点，则该点为核心点,这些点都是在簇内的

– 稠密区域边缘上的点(边界点) :在半径Eps内点的数量小于MinPts，但是在核心点的邻居

– 稀疏区域中的点(噪声或背景点)：任何不是核心点或边界点的点.

Eps邻域：给定对象半径Eps内的邻域称为该对象的Eps邻域，我们用表示点p的Eps-半径内的点的集合，即:

核心对象：如果对象的Eps邻域至少包含最小数目MinPts的对象，则称该对象为核心对象。
边界点：边界点不是核心点，但落在某个核心点的邻域内。
噪音点：既不是核心点，也不是边界点的任何点

• DBSCAN通过检查数据集中每点的Eps邻域来搜索簇，如果点p的Eps邻域包含的点多于MinPts个，则创建一个以p为核心对象的簇。
• 然后，DBSCAN迭代地聚集从这些核心对象直接密度可达的对象，这个过程可能涉及一些密度可达簇的合并。
• 当没有新的点添加到任何簇时，该过程结束

• 时间复杂度
– DBSCAN的基本时间复杂度是 O(N*找出Eps领域中的点所需要的时间), N是点的个数。最坏情况下时间复杂度是O(N^2)
2) – 在低维空间数据中,有一些数据结构如KD树，使得可以有效的检索特定点给定距离内的所有点，时间复杂度可以降低到O(NlogN)

空间复杂度
– 低维或高维数据中，其空间都是O(N)，对于每个点它只需要维持少量数据，即簇标号和每个点的标识(核心点或边界点或噪音点)

优点
– 基于密度定义，相对抗噪音，能处理任意形状和大小的簇
• 缺点
– 当簇的密度变化太大时，会有麻烦
– 对于高维问题，密度定义是个比较麻烦的问题

sklearn

sklearn-dbscan

import pandas as pd
import matplotlib.pyplot as plt
from sklearn.cluster import DBSCAN
from sklearn import metrics, preprocessing
data_path = 'data.csv'

# 读取数据文件
data_frame = pd.read_csv(data_path, encoding='gbk')


# DBSCAN聚类
def dbscan_cluster(x_label, y_label):

    # 生成DBSCAN模型
    clu = DBSCAN(eps=1, min_samples=5)

    X_value = data_frame[[x_label, y_label]].values

    # 开始进行DBSCAN聚类
    clu.fit(X_value)
    # 输出样本所属的簇
    print('样本所属簇编号:', clu.labels_)

    # 可视化聚类属性(散点图)

    # 参数设置
    plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
    plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号

    # 以簇编号作为颜色区分依据
    plt.scatter(data_frame[x_label], data_frame[y_label], c=clu.labels_)

    plt.title('DBSCAN聚类结果')
    plt.xlabel(x_label)
    plt.ylabel(y_label)
    plt.show()


if __name__ == '__main__':
    dbscan_cluster('当月MOU', '当月DOU')

sklearn_k-means

import pandas as pd
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
import numpy as np
from scipy.spatial.distance import pdist
from sklearn import metrics, preprocessing

data_path = 'data.csv'

# 读取数据文件
data_frame = pd.read_csv(data_path, encoding='gbk')

# 获取字段名
cols = list(data_frame.columns)


# 数据本身的散点图
def draw_scatter(x_label, y_label):
    # 绘图参数的设置
    plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
    plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
    plt.scatter(data_frame[x_label], data_frame[y_label])

    plt.xlabel(x_label)
    plt.ylabel(y_label)

    plt.title('{0}-{1}散点图'.format(x_label, y_label))
    plt.show()


# K-Means聚类
def k_means_cluster(x_label, y_label, k):
    # 调用sklearn库生成K-Means模型
    #n_clusters聚集几个簇 max_iter最大迭代次数
    clu = KMeans(n_clusters=k, max_iter=300)
    #获取数据集
    X_value = data_frame[[x_label, y_label]].values
    print(type(X_value))
    # 开始进行K-Means聚类
    clu.fit(X_value)

    # 输出样本所属的簇
    print('样本所属簇编号:', clu.labels_)
    print(clu.labels_[100:200])
    # 输出簇中心坐标
    print('簇中心坐标:', clu.cluster_centers_)

    # 计算V值 （V=簇内平均误差平方和/簇间平均距离）
    v_value = clu.inertia_ / (k * np.average(pdist(clu.cluster_centers_)))
    print('v值{0}'.format(v_value))

    # 可视化聚类属性(散点图)

    # 参数设置
    plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
    plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号

    # 以簇编号作为颜色区分依据
    plt.scatter(data_frame[x_label], data_frame[y_label], c=clu.labels_)

    plt.title('K={0}聚类结果'.format(k))
    plt.xlabel(x_label)
    plt.ylabel(y_label)
    plt.show()


# 思想：手肘法
# 随着聚类数k的增大，样本划分会更加精细，每个簇的聚合程度会逐渐提高，那么误差平方和SSE自然会逐渐变小。
# 并且，当k小于真实聚类数时，由于k的增大会大幅增加每个簇的聚合程度，故SSE的下降幅度会很大，而当k到达真实聚类数时，
# 再增加k所得到的聚合程度回报会迅速变小，所以SSE的下降幅度会骤减，然后随着k值的继续增大而趋于平缓，
# 也就是说SSE和k的关系图是一个手肘的形状，而这个肘部对应的k值就是数据的真实聚类数。当然，这也是该方法被称为手肘法的原因。

# 对比不同的K对V值的影响
def compare_k(x_label, y_label):

    k_ls = np.arange(1, 15)
    v_ls = []

    for k in k_ls:

        # 生成K-Means模型
        clu = KMeans(n_clusters=k, max_iter=300)

        X_value = data_frame[[x_label, y_label]].values
        # 开始进行K-Means聚类
        clu.fit(X_value)

        # 计算V值 （V=簇内平均误差平方和/簇间平均距离）
        v_value = clu.inertia_ / (k * np.average(pdist(clu.cluster_centers_)))

        # 添加到v_ls中
        v_ls.append(v_value)

    # 参数设置
    plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
    plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
    print(v_ls)
    # 画k-v折线图
    plt.plot(k_ls, v_ls)

    plt.title('聚类个数对V值的影响')
    plt.xlabel('聚类个数')
    plt.ylabel('V值')
    plt.show()


# 归一化
def normalize_data(x_label, y_label, k):

    # 生成K-Means模型
    clu = KMeans(n_clusters=k, max_iter=300)

    # 归一化
    # scale_X = data_frame[[x_label, y_label]].apply(lambda x: x/x.max()).values
    min_max_scaler = preprocessing.MinMaxScaler()
    X_train_minmax = min_max_scaler.fit_transform(data_frame[[x_label, y_label]].values)
    # X_value = data_frame[[x_label, y_label]].values
    print(X_train_minmax)
    # 开始进行K-Means聚类
    clu.fit(X_train_minmax)
    # 输出样本所属的簇
    print('样本所属簇编号:', clu.labels_)
    # 输出簇中心坐标
    print('簇中心坐标:', clu.cluster_centers_)

    # 计算V值 （V=簇内平均误差平方和/簇间平均距离）
    v_value = clu.inertia_ / (k * np.average(pdist(clu.cluster_centers_)))
    print('v值{0}'.format(v_value))

    # 可视化聚类属性(散点图)

    # 参数设置
    plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
    plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号

    # 以簇编号作为颜色区分依据
    plt.scatter(X_train_minmax[:, 0], X_train_minmax[:, 1], c=clu.labels_)

    plt.title('K={0}聚类结果'.format(k))
    plt.xlabel(x_label)
    plt.ylabel(y_label)
    plt.show()

if __name__ == '__main__':
    pass
    # draw_scatter('当月MOU', '当月DOU')
    # k_means_cluster('当月MOU', '当月DOU', 3)
    compare_k('当月MOU', '当月DOU')
    # normalize_data('当月MOU', '当月DOU', 3)

sklearn_minibatchk-means

import time
import numpy as np
import matplotlib.pyplot as plt

from sklearn.cluster import MiniBatchKMeans, KMeans
from sklearn.metrics.pairwise import pairwise_distances_argmin
from sklearn.datasets.samples_generator import make_blobs

# #############################################################################
# 产生样本数据
np.random.seed(0)

batch_size = 45
centers = [[1, 1], [-1, -1], [1, -1]]  # 三种聚类的中心
n_clusters = len(centers)
X, labels_true = make_blobs(n_samples=30000, centers=centers, cluster_std=0.7)  # 生成样本随机数

# #############################################################################
# k均值聚类

k_means = KMeans(init='k-means++', n_clusters=3, n_init=10)
begin_time = time.time()  # 记录训练开始时间
k_means.fit(X) # 聚类模型
t_batch = time.time() - begin_time  # 记录训练用时
print('k均值聚类时长：',t_batch)
# #############################################################################
# 小批量k均值聚类
# batch_size为每次更新使用的样本数
mbk = MiniBatchKMeans(init='k-means++', n_clusters=3, batch_size=batch_size,
                      n_init=10, max_no_improvement=10, verbose=0)
begin_time = time.time()  # 记录训练开始时间
mbk.fit(X) # 聚类模型
t_mini_batch = time.time() -  begin_time  # 记录训练用时
print('小批量k均值聚类时长：',t_mini_batch)
# #############################################################################
# 结果可视化
fig = plt.figure(figsize=(16, 6))  # 窗口大小
fig.subplots_adjust(left=0.02, right=0.98, bottom=0.05, top=0.9)  # # 窗口四周留白
# colors = ['#4EACC5', '#FF9C34', '#4E9A06']  # 三种聚类的颜色
colors = ['r', 'y', 'b']  # 三种聚类的颜色
# 在两种聚类算法中，样本的所属类标号和聚类中心(返回y的索引)
k_means_cluster_centers = np.sort(k_means.cluster_centers_, axis=0)  # 三个聚类点排序
mbk_means_cluster_centers = np.sort(mbk.cluster_centers_, axis=0)  # 三个聚类点排序
k_means_labels = pairwise_distances_argmin(X, k_means_cluster_centers)  # 计算X中每个样本与k_means_cluster_centers中的哪个样本最近。也就是获取所有对象的所属的类标签
mbk_means_labels = pairwise_distances_argmin(X, mbk_means_cluster_centers)  # 计算X中每个样本与k_means_cluster_centers中的哪个样本最近。也就是获取所有对象的所属的类标签
order = pairwise_distances_argmin(k_means_cluster_centers,mbk_means_cluster_centers)  # 计算k均值聚类点相对于小批量k均值聚类点的索引。因为要比较两次聚类的结果的区别，所以类标号要对应上


# 绘制KMeans
ax = fig.add_subplot(1, 3, 1)
for k, col in zip(range(n_clusters), colors):
    my_members = k_means_labels == k  # 获取属于当前类别的样本
    cluster_center = k_means_cluster_centers[k]  # 获取当前聚类中心
    ax.plot(X[my_members, 0], X[my_members, 1], 'w',markerfacecolor=col, marker='.') # 绘制当前聚类的样本点
    ax.plot(cluster_center[0], cluster_center[1], 'o', markerfacecolor=col,markeredgecolor='k', markersize=6) # 绘制聚类中心点
ax.set_title('KMeans')
ax.set_xticks(())
ax.set_yticks(())
plt.text(-3.5, 1.8,  'train time: %.2fs\ninertia: %f' % (t_batch, k_means.inertia_))

# 绘制MiniBatchKMeans
ax = fig.add_subplot(1, 3, 2)
for k, col in zip(range(n_clusters), colors):
    my_members = mbk_means_labels == k # 获取属于当前类别的样本
    cluster_center = mbk_means_cluster_centers[k] # 获取当前聚类中心
    ax.plot(X[my_members, 0], X[my_members, 1], 'w',markerfacecolor=col, marker='.') # 绘制当前聚类的样本点
    ax.plot(cluster_center[0], cluster_center[1], 'o', markerfacecolor=col,markeredgecolor='k', markersize=6) # 绘制聚类中心点
ax.set_title('MiniBatchKMeans')
ax.set_xticks(())
ax.set_yticks(())
plt.text(-3.5, 1.8, 'train time: %.2fs\ninertia: %f' %(t_mini_batch, mbk.inertia_))

# 初始化两次结果中
different = (mbk_means_labels == 4)
ax = fig.add_subplot(1, 3, 3)

for k in range(n_clusters):
    different += ((k_means_labels == k) != (mbk_means_labels == order[k]))  # 将两种聚类算法中聚类结果不一样的样本设置为true，聚类结果相同的样本设置为false

identic = np.logical_not(different)  # 向量取反，也就是聚类结果相同设置true，聚类结果不相同设置为false

ax.plot(X[identic, 0], X[identic, 1], 'w',markerfacecolor='#bbbbbb', marker='.') # 绘制聚类结果相同的样本点
ax.plot(X[different, 0], X[different, 1], 'w',markerfacecolor='m', marker='.') # 绘制聚类结果不同的样本点
ax.set_title('Difference')
ax.set_xticks(())
ax.set_yticks(())

plt.show()