深入浅出对话系统——自己实现Transformer
引言
我们在上篇文章中学习了的Transformer库,为了更好地理解Transformer,本文通过PyTorch实现一个Transformer,并完成中英文机器翻译任务。
导包与初始化
import copy
import math
import matplotlib.pyplot as plt
import numpy as np
import os
import seaborn as sns
import time
import torch
import torch.nn as nn
import torch.nn.functional as F
from collections import Counter
from langconv import Converter
from nltk import word_tokenize
from torch.autograd import Variable
其中nltk的安装可以参考文章 https://zhuanlan.zhihu.com/p/347931749
或import nltk nltk.set_proxy('http://proxy.example.com:3128', ('USERNAME', 'PASSWORD')) nltk.download()
初始化参数设置:
# 初始化参数设置
PAD = 0 # padding占位符的索引
UNK = 1 # 未登录词标识符的索引
BATCH_SIZE = 128 # 批次大小
EPOCHS = 20 # 训练轮数
LAYERS = 6 # transformer中encoder、decoder层数
H_NUM = 8 # 多头注意力个数
D_MODEL = 256 # 输入、输出词向量维数
D_FF = 1024 # feed forward全连接层维数
DROPOUT = 0.1 # dropout比例
MAX_LENGTH = 60 # 语句最大长度
TRAIN_FILE = 'nmt/en-cn/train.txt' # 训练集
DEV_FILE = "nmt/en-cn/dev.txt" # 验证集
SAVE_FILE = 'save/model.pt' # 模型保存路径
DEVICE = torch.device("cuda" if torch.cuda.is_available() else "cpu")
数据集下载
下载数据集
数据预处理
主要做的事是加载数据、分词、构建词表和批次划分。对中文语句一般以字为单位进行切分,所以不需要对中文语句分词。
训练数据是长这样子的:
Anyone can do that. 任何人都可以做到。
How about another piece of cake? 要不要再來一塊蛋糕?
She married him. 她嫁给了他。
I don't like learning irregular verbs. 我不喜欢学习不规则动词。
It's a whole new ball game for me. 這對我來說是個全新的球類遊戲。
He's sleeping like a baby. 他正睡着,像个婴儿一样。
He can play both tennis and baseball. 他既会打网球,又会打棒球。
We should cancel the hike. 我們應該取消這次遠足。
He is good at dealing with children. 他擅長應付小孩子。
首先我们按批次对数据进行填充,使得同一批次内的数据长度对齐。
def seq_padding(X, padding=PAD):
"""
按批次(batch)对数据填充、长度对齐
"""
# 计算该批次各条样本语句长度
lens = [len(x) for x in X]
# 获取该批次样本中语句长度最大值
max_len = max(lens)
# 遍历该批次样本,如果语句长度小于最大长度,则用padding填充
return np.array([
np.concatenate([x, [padding] * (max_len - len(x))]) if len(x) < max_len else x for x in X
])
不同批次内的最大长度可以不一致。
如上所见,这里的中文为繁体,所以我们还需要做简繁转换:
def cht_to_chs(sent):
sent = Converter("zh-hans").convert(sent)
sent.encode("utf-8")
return sent
下面来准备数据:
class PrepareData:
def __init__(self, train_file, dev_file):
# 读取数据、分词
self.train_en, self.train_cn = self.load_data(train_file)
self.dev_en, self.dev_cn = self.load_data(dev_file)
# 构建词表
self.en_word_dict, self.en_total_words, self.en_index_dict = \
self.build_dict(self.train_en)
self.cn_word_dict, self.cn_total_words, self.cn_index_dict = \
self.build_dict(self.train_cn)
# 单词映射为索引
self.train_en, self.train_cn = self.word2id(self.train_en, self.train_cn, self.en_word_dict, self.cn_word_dict)
self.dev_en, self.dev_cn = self.word2id(self.dev_en, self.dev_cn, self.en_word_dict, self.cn_word_dict)
# 划分批次、填充、掩码
self.train_data = self.split_batch(self.train_en, self.train_cn, BATCH_SIZE)
self.dev_data = self.split_batch(self.dev_en, self.dev_cn, BATCH_SIZE)
def load_data(self, path):
"""
读取英文、中文数据
对每条样本分词并构建包含起始符和终止符的单词列表
形式如:en = [['BOS', 'i', 'love', 'you', 'EOS'], ['BOS', 'me', 'too', 'EOS'], ...]
cn = [['BOS', '我', '爱', '你', 'EOS'], ['BOS', '我', '也', '是', 'EOS'], ...]
"""
en = []
cn = []
with open(path, mode="r", encoding="utf-8") as f:
for line in f.readlines():
sent_en, sent_cn = line.strip().split("\t")
sent_en = sent_en.lower()
sent_cn = cht_to_chs(sent_cn)
sent_en = ["BOS"] + word_tokenize(sent_en) + ["EOS"]
# 中文按字符切分
sent_cn = ["BOS"] + [char for char in sent_cn] + ["EOS"]
en.append(sent_en)
cn.append(sent_cn)
return en, cn
def build_dict(self, sentences, max_words=5e4):
"""
构造分词后的列表数据
构建单词-索引映射(key为单词,value为id值)
"""
# 统计数据集中单词词频
word_count = Counter([word for sent in sentences for word in sent])
# 按词频保留前max_words个单词构建词典
# 添加UNK和PAD两个单词
ls = word_count.most_common(int(max_words))
total_words = len(ls) + 2
word_dict = {w[0]: index + 2 for index, w in enumerate(ls)}
word_dict['UNK'] = UNK
word_dict['PAD'] = PAD
# 构建id2word映射
index_dict = {v: k for k, v in word_dict.items()}
return word_dict, total_words, index_dict
def word2id(self, en, cn, en_dict, cn_dict, sort=True):
"""
将英文、中文单词列表转为单词索引列表
`sort=True`表示以英文语句长度排序,以便按批次填充时,同批次语句填充尽量少
"""
length = len(en)
# 单词映射为索引
out_en_ids = [[en_dict.get(word, UNK) for word in sent] for sent in en]
out_cn_ids = [[cn_dict.get(word, UNK) for word in sent] for sent in cn]
# 按照语句长度排序,使批次内的长度尽可能一致
def len_argsort(seq):
"""
传入一系列语句数据(分好词的列表形式),
按照语句长度排序后,返回排序后原来各语句在数据中的索引下标
"""
return sorted(range(len(seq)), key=lambda x: len(seq[x]))
# 按相同顺序对中文、英文样本排序
if sort:
# 以英文语句长度排序
sorted_index = len_argsort(out_en_ids)
out_en_ids = [out_en_ids[idx] for idx in sorted_index]
out_cn_ids = [out_cn_ids[idx] for idx in sorted_index]
return out_en_ids, out_cn_ids
def split_batch(self, en, cn, batch_size, shuffle=True):
"""
划分批次
`shuffle=True`表示对各批次顺序随机打乱
"""
# 每隔batch_size取一个索引作为后续batch的起始索引
idx_list = np.arange(0, len(en), batch_size)
# 起始索引随机打乱
if shuffle:
np.random.shuffle(idx_list)
# 存放所有批次的语句索引
batch_indexs = []
for idx in idx_list:
"""
形如[array([4, 5, 6, 7]),
array([0, 1, 2, 3]),
array([8, 9, 10, 11]),
...]
"""
# 起始索引最大的批次可能发生越界,要限定其索引
batch_indexs.append(np.arange(idx, min(idx + batch_size, len(en))))
# 构建批次列表
batches = []
for batch_index in batch_indexs:
# 按当前批次的样本索引采样
batch_en = [en[index] for index in batch_index]
batch_cn = [cn[index] for index in batch_index]
# 对当前批次中所有语句填充、对齐长度
# 维度为:batch_size * 当前批次中语句的最大长度
batch_cn = seq_padding(batch_cn)
batch_en = seq_padding(batch_en)
# 将当前批次添加到批次列表
# Batch类用于实现注意力掩码
batches.append(Batch(batch_en, batch_cn))
return batches
数据准备好了,下面我们正式开始了解Transformer模型。
Transformer模型概述
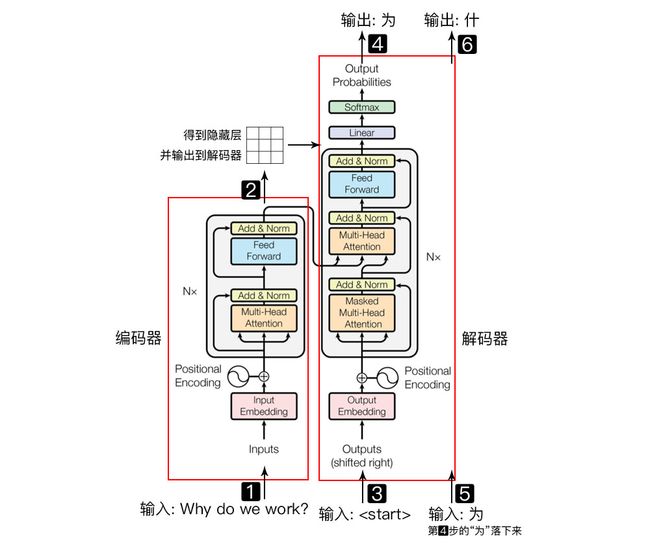
Transformer相比LSTM而言最大的优势在于可以并行训练,极大地加快计算效率。通过位置编码理解语言的顺序,使用自注意力机制和全连接层前向计算,整个架构中没有循环结构。
借鉴了seq2seq,Transformer模型由编码器和解码器组成。
- 编码器(encoder): 将自然语言序列编码成隐藏层表示
- 解码器(decoder):将隐藏层表示映射为自然语言序列,从而解决各种任务,如情感分析、命名实体识别和机器翻译等。
下面我们来详细了解其中的组件。
词嵌入层
在编码器和解码器中都有词嵌入层,用于将输入、输出ont-hot向量映射为词嵌入向量。可以随机初始化进行学习,也可以加载预训练的词向量。
它的实现比较简单:
class Embeddings(nn.Module):
def __init__(self, d_model, vocab):
super(Embeddings, self).__init__()
# Embedding层
self.embed = nn.Embedding(vocab, d_model)
# Embedding维数
self.d_model = d_model
def forward(self, x):
# 返回x的词向量(需要乘以math.sqrt(d_model))
return self.embed(x) * math.sqrt(self.d_model)
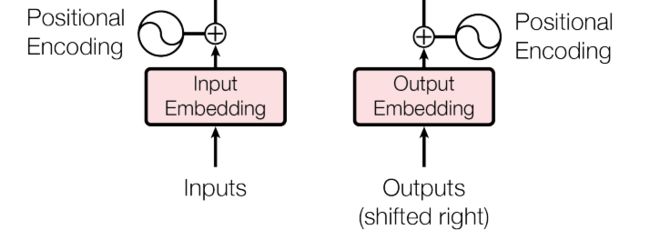
位置编码
由于Transformer的输入采用并行方式,缺少单词位置信息。因此需要增加包含单词位置信息的位置编码层。
位置编码(positional encoding):位置编码向量与词向量维度相同, max_seq_len × embedding_dim \text{max\_seq\_len} \times \text{embedding\_dim} max_seq_len×embedding_dim。
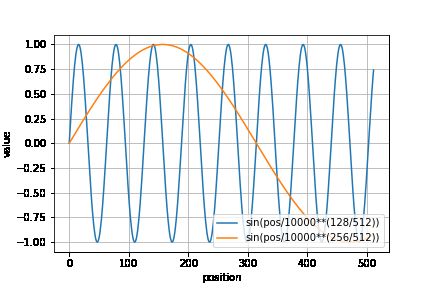
Transformer原文中使用正、余弦函数的线性变换对单词位置编码:
PE p o s , 2 i = sin ( p o s 1000 0 2 i / d model ) PE ( p o s , 2 i + 1 ) = cos ( p o s 1000 0 2 i / d model ) (1) \text{PE}_{pos, 2i} = \sin \left( \frac{pos}{10000^{2i / d_{\text{model}}}} \right) \\ \text{PE}_{(pos,2i + 1)} = \cos \left( \frac{pos}{10000^{2i / d_{\text{model}}}} \right)\tag{1} PEpos,2i=sin(100002i/dmodelpos)PE(pos,2i+1)=cos(100002i/dmodelpos)(1)
为了使用序列顺序信息,作者提出了利用不同频率的正弦和余弦函数表示位置编码。序列顺序信息重要性是不言而喻的。比如以下两个句子:
我爱你
你爱我
作者用词嵌入向量➕位置编码得到输入向量,这里简单解释一下为什么作者选用正弦和余弦函数。
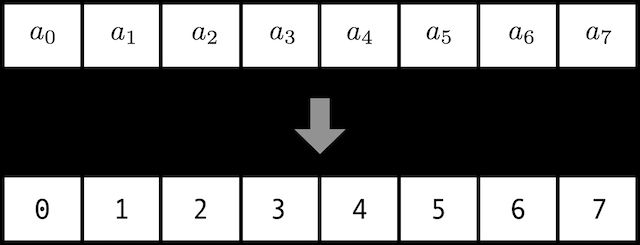
假设我们自己设置位置编码,一个简单的办法是增加索引到词嵌入向量。
假设 a a a表示词嵌入向量。这种方法有一个很大的问题,即句子越长,后面单词的序号就越大,而且索引值过大,可能会掩盖了嵌入向量的“光辉”。
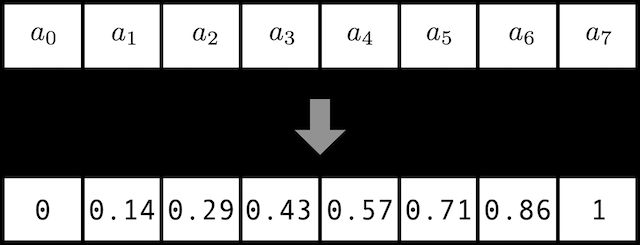
你说序号太大了,那么我把每个序号都除以句子长度总不大了吧。听起来不错,但是这引入了另一个问题,就是由于句子的长度不同,导致同样的值可能代表不同的意思,这样让我们的模型很困惑。比如 0.8 0.8 0.8在句长为 5 5 5的句子中表示第 4 4 4个单词,但是在句长为 20 20 20的句子中表示第 16 16 16个单词。
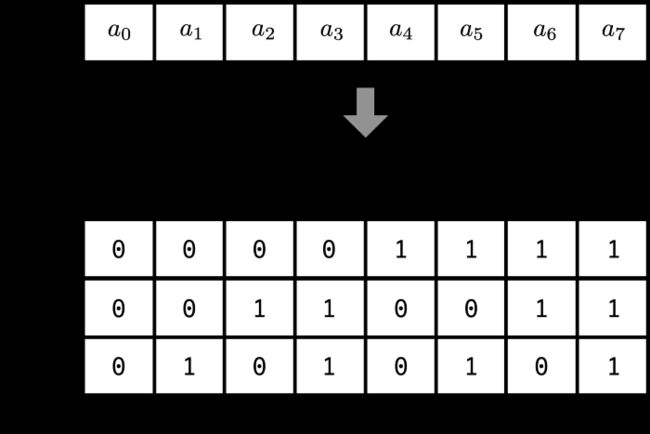
因为我们上面句子长度为8, 2 3 = 8 2^3=8 23=8,何不用二进制来表示顺序信息呢?如上图所示。从上往下看,比如4对应“100”,5对应“101”。
这里我们用3位表示就足够了,一般我们可以设置成 d m o d e l d_{model} dmodel。
那这种方法就很好了吗?
- 我们仍然没有完全归一化。我们想要位置编码也符合某种分布。最好让正负数的分布均匀,这个很好实现,可以通过函数 f ( x ) = 2 x − 1 f(x)=2x-1 f(x)=2x−1,将[0,1] -> [-1,1]
- 我们的二进制向量来自离散函数,而不是连续函数的离散化。
我们的位置编码应该满足下面的要求:
- 对于每个时间步(句子中的单词位置),它都能输出独一无二的编码
- 任意两个时间步之间的距离都应该是一个常量,而不因句子长度而变
- 我们的模型应该能轻易地泛化到更长的句子,它的值应该是有界的
- 位置编码必须是确定的
作者提出的编码方式是一个简单且天才的技术,满足了上面所有的要求。首先,它不是一个标量,而是一个包含特定位置信息的 d d d维向量。其次,该编码并没有整合到模型中。相反,这个向量用于为每个单词设置关于它在句子中位置的信息。换言之,通过注入单词的顺序来增强模型的输入。
令 t t t为输入序列中某个位置, p t → \overset{\rightarrow}{p_t} pt→是该位置的位置编码, d d d是向量维度。 f f f是通过以下公式产生位置编码向量的函数:
p t ⃗ ( i ) = f ( t ) ( i ) : = { sin ( ω k ⋅ t ) , 若 i = 2 k cos ( ω k ⋅ t ) , 若 i = 2 k + 1 \vec{p_t}^{(i)} = f(t)^{(i)} := \begin{cases} \sin({\omega_k} \cdot t), & \text{若}\ i = 2k \\ \cos({\omega_k} \cdot t), & \text{若}\ i = 2k + 1 \end{cases} pt(i)=f(t)(i):={sin(ωk⋅t),cos(ωk⋅t),若 i=2k若 i=2k+1
其中
ω k = 1 1000 0 2 k / d \omega_k = \frac{1}{10000^{2k / d}} ωk=100002k/d1
由该式子可以看出,频率是随着向量维度降低的(由 1 2 π \frac{1}{2\pi} 2π1降低成 1 10000 ⋅ 2 π \frac{1}{10000 \cdot 2\pi} 10000⋅2π1)。因此波长形成一个从 2 π 2 \pi 2π到 10000 ⋅ 2 π 10000 \cdot 2\pi 10000⋅2π的等比数列。
我们也能想象位置编码 p t ⃗ \vec{p_t} pt是一个包含各个频率的正弦和余弦向量,其中 d d d可以被 2 2 2整除。
p t ⃗ = [ sin ( ω 1 ⋅ t ) cos ( ω 1 ⋅ t ) sin ( ω 2 ⋅ t ) cos ( ω 2 ⋅ t ) ⋮ sin ( ω d / 2 ⋅ t ) cos ( ω d / 2 ⋅ t ) ] d × 1 \vec{p_t} = \begin{bmatrix} \sin({\omega_1}\cdot t)\\ \cos({\omega_1}\cdot t)\\ \\ \sin({\omega_2}\cdot t)\\ \cos({\omega_2}\cdot t)\\ \\ \vdots\\ \\ \sin({\omega_{d/2}}\cdot t)\\ \cos({\omega_{d/2}}\cdot t) \end{bmatrix}_{d \times 1} pt=⎣ ⎡sin(ω1⋅t)cos(ω1⋅t)sin(ω2⋅t)cos(ω2⋅t)⋮sin(ωd/2⋅t)cos(ωd/2⋅t)⎦ ⎤d×1
为什么正弦和余弦的组合可以表示顺序。假设我们用二进制来表示数字。
0 : 0 0 0 0 8 : 1 0 0 0 1 : 0 0 0 1 9 : 1 0 0 1 2 : 0 0 1 0 10 : 1 0 1 0 3 : 0 0 1 1 11 : 1 0 1 1 4 : 0 1 0 0 12 : 1 1 0 0 5 : 0 1 0 1 13 : 1 1 0 1 6 : 0 1 1 0 14 : 1 1 1 0 7 : 0 1 1 1 15 : 1 1 1 1 \begin{aligned} 0: \ \ \ \ \color{orange}{\texttt{0}} \ \ \color{green}{\texttt{0}} \ \ \color{blue}{\texttt{0}} \ \ \color{red}{\texttt{0}} & & 8: \ \ \ \ \color{orange}{\texttt{1}} \ \ \color{green}{\texttt{0}} \ \ \color{blue}{\texttt{0}} \ \ \color{red}{\texttt{0}} \\ 1: \ \ \ \ \color{orange}{\texttt{0}} \ \ \color{green}{\texttt{0}} \ \ \color{blue}{\texttt{0}} \ \ \color{red}{\texttt{1}} & & 9: \ \ \ \ \color{orange}{\texttt{1}} \ \ \color{green}{\texttt{0}} \ \ \color{blue}{\texttt{0}} \ \ \color{red}{\texttt{1}} \\ 2: \ \ \ \ \color{orange}{\texttt{0}} \ \ \color{green}{\texttt{0}} \ \ \color{blue}{\texttt{1}} \ \ \color{red}{\texttt{0}} & & 10: \ \ \ \ \color{orange}{\texttt{1}} \ \ \color{green}{\texttt{0}} \ \ \color{blue}{\texttt{1}} \ \ \color{red}{\texttt{0}} \\ 3: \ \ \ \ \color{orange}{\texttt{0}} \ \ \color{green}{\texttt{0}} \ \ \color{blue}{\texttt{1}} \ \ \color{red}{\texttt{1}} & & 11: \ \ \ \ \color{orange}{\texttt{1}} \ \ \color{green}{\texttt{0}} \ \ \color{blue}{\texttt{1}} \ \ \color{red}{\texttt{1}} \\ 4: \ \ \ \ \color{orange}{\texttt{0}} \ \ \color{green}{\texttt{1}} \ \ \color{blue}{\texttt{0}} \ \ \color{red}{\texttt{0}} & & 12: \ \ \ \ \color{orange}{\texttt{1}} \ \ \color{green}{\texttt{1}} \ \ \color{blue}{\texttt{0}} \ \ \color{red}{\texttt{0}} \\ 5: \ \ \ \ \color{orange}{\texttt{0}} \ \ \color{green}{\texttt{1}} \ \ \color{blue}{\texttt{0}} \ \ \color{red}{\texttt{1}} & & 13: \ \ \ \ \color{orange}{\texttt{1}} \ \ \color{green}{\texttt{1}} \ \ \color{blue}{\texttt{0}} \ \ \color{red}{\texttt{1}} \\ 6: \ \ \ \ \color{orange}{\texttt{0}} \ \ \color{green}{\texttt{1}} \ \ \color{blue}{\texttt{1}} \ \ \color{red}{\texttt{0}} & & 14: \ \ \ \ \color{orange}{\texttt{1}} \ \ \color{green}{\texttt{1}} \ \ \color{blue}{\texttt{1}} \ \ \color{red}{\texttt{0}} \\ 7: \ \ \ \ \color{orange}{\texttt{0}} \ \ \color{green}{\texttt{1}} \ \ \color{blue}{\texttt{1}} \ \ \color{red}{\texttt{1}} & & 15: \ \ \ \ \color{orange}{\texttt{1}} \ \ \color{green}{\texttt{1}} \ \ \color{blue}{\texttt{1}} \ \ \color{red}{\texttt{1}} \\ \end{aligned} 0: 0 0 0 01: 0 0 0 12: 0 0 1 03: 0 0 1 14: 0 1 0 05: 0 1 0 16: 0 1 1 07: 0 1 1 18: 1 0 0 09: 1 0 0 110: 1 0 1 011: 1 0 1 112: 1 1 0 013: 1 1 0 114: 1 1 1 015: 1 1 1 1
可以看到,随着十进制数的增加,每个位的变化率是不一样的,越低位的变化越快,红色位 0 0 0和 1 1 1,每个数字都会变化一次;
而黄色位,每 8 8 8个数字才会变化一次。
但是二进制值的 0 , 1 0,1 0,1是离散的,浪费了它们之间无限的浮点数。所以我们使用它们的连续浮动版本-正弦函数。
此外,通过降低它们的频率,我们可以从红色位变成黄色位,这样就实现了这种低位到高位的变换。如下图所示:
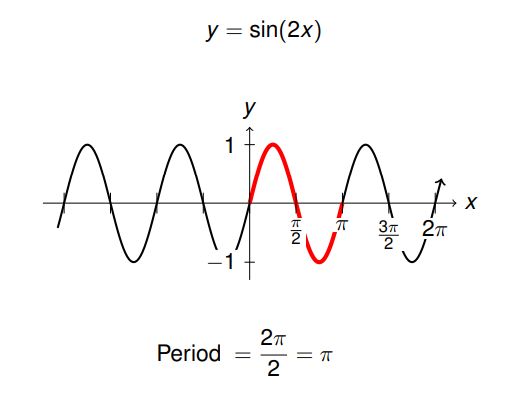
下面补充一下波长和频率的计算:
对于正弦函数来说,波长(周期)的计算如上图。任意 sin ( B x ) \sin (Bx) sin(Bx)的波长是 2 π B \frac{2\pi}{B} B2π,频率是 B 2 π \frac{B}{2\pi} 2πB。
最后,通过设置位置编码的维度和词嵌入向量的维度一致,可以将位置编码加入到词向量。
原文中提到
对于任何固定的偏移量 k k k, P E p o s + k PE_{pos + k} PEpos+k都要能表示为 P E p o s PE_{pos} PEpos的一个线性函数。
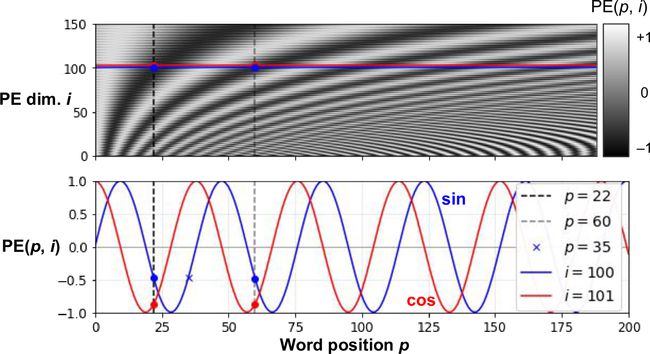
上图顶部是长度为200、维度为150的序列转置后的位置矩阵 P E PE PE,上图底部是所 p p p在的位置向量中的第 i i i个分量位置的正弦余弦函数图像,来自 Hands-on Machine Learning with Scikit Learn, Keras, TensorFlow: Concepts, Tools and Techniques to Build Intelligent Systems 2nd Edition
对每个频率 ω k \omega_k ωk相应的正-余弦对,存在一个线性转换 M ∈ R 2 × 2 M \in \mathbb{R}^{2\times2} M∈R2×2:
M . [ sin ( ω k ⋅ t ) cos ( ω k ⋅ t ) ] = [ sin ( ω k ⋅ ( t + ϕ ) ) cos ( ω k ⋅ ( t + ϕ ) ) ] M.\begin{bmatrix} \sin(\omega_k\cdot t) \\ \cos(\omega_k \cdot t) \end{bmatrix} = \begin{bmatrix} \sin(\omega_k \cdot (t + \phi)) \\ \cos(\omega_k \cdot (t + \phi)) \end{bmatrix} M.[sin(ωk⋅t)cos(ωk⋅t)]=[sin(ωk⋅(t+ϕ))cos(ωk⋅(t+ϕ))]
证明:
假设 M M M是一个 2 × 2 2 \times 2 2×2的矩阵,我们想要找到其中的元素 u 1 , v 1 , u 2 , v 2 u_1,v_1,u_2,v_2 u1,v1,u2,v2满足:
[ u 1 v 1 u 2 v 2 ] ⋅ [ sin ( ω k ⋅ t ) cos ( ω k ⋅ t ) ] = [ sin ( ω k ⋅ ( t + ϕ ) ) cos ( ω k ⋅ ( t + ϕ ) ) ] \begin{bmatrix} u_1 & v_1 \\ u_2 & v_2 \end{bmatrix} \cdot \begin{bmatrix} \sin(\omega_k \cdot t) \\ \cos(\omega_k \cdot t) \end{bmatrix} = \begin{bmatrix} \sin(\omega_k \cdot (t + \phi)) \\ \cos(\omega_k \cdot (t + \phi)) \end{bmatrix} [u1u2v1v2]⋅[sin(ωk⋅t)cos(ωk⋅t)]=[sin(ωk⋅(t+ϕ))cos(ωk⋅(t+ϕ))]
利用三角函数两角和的正弦公式和余弦公式,得到:
[ u 1 v 1 u 2 v 2 ] ⋅ [ sin ( ω k ⋅ t ) cos ( ω k ⋅ t ) ] = [ sin ( ω k ⋅ t ) cos ( ω k ⋅ ϕ ) + cos ( ω k ⋅ t ) sin ( ω k ⋅ ϕ ) cos ( ω k ⋅ t ) cos ( ω k ⋅ ϕ ) − sin ( ω k ⋅ t ) sin ( ω k ⋅ ϕ ) ] \begin{bmatrix} u_1 & v_1 \\ u_2 & v_2 \end{bmatrix} \cdot \begin{bmatrix} \sin(\omega_k \cdot t) \\ \cos(\omega_k \cdot t) \end{bmatrix} = \begin{bmatrix} \sin(\omega_k \cdot t)\cos(\omega_k \cdot \phi) + \cos(\omega_k \cdot t)\sin(\omega_k \cdot \phi) \\ \cos(\omega_k \cdot t)\cos(\omega_k \cdot \phi) - \sin(\omega_k \cdot t)\sin(\omega_k \cdot \phi) \end{bmatrix} [u1u2v1v2]⋅[sin(ωk⋅t)cos(ωk⋅t)]=[sin(ωk⋅t)cos(ωk⋅ϕ)+cos(ωk⋅t)sin(ωk⋅ϕ)cos(ωk⋅t)cos(ωk⋅ϕ)−sin(ωk⋅t)sin(ωk⋅ϕ)]
得到下面两个等式:
u 1 sin ( ω k ⋅ t ) + v 1 cos ( ω k ⋅ t ) = cos ( ω k ⋅ ϕ ) sin ( ω k ⋅ t ) + sin ( ω k ⋅ ϕ ) cos ( ω k ⋅ t ) u 2 sin ( ω k ⋅ t ) + v 2 cos ( ω k ⋅ t ) = − sin ( ω k ⋅ ϕ ) sin ( ω k ⋅ t ) + cos ( ω k ⋅ ϕ ) cos ( ω k ⋅ t ) \small \begin{aligned} u_1 \sin(\omega_k \cdot t) + v_1 \cos(\omega_k \cdot t) = & \ \ \ \ \cos(\omega_k \cdot\phi)\sin(\omega_k \cdot t) + \sin(\omega_k \cdot\phi)\cos(\omega_k \cdot t) \\ u_2 \sin(\omega_k \cdot t) + v_2 \cos(\omega_k \cdot t) = & - \sin(\omega_k \cdot \phi)\sin(\omega_k \cdot t) + \cos(\omega_k \cdot\phi)\cos(\omega_k \cdot t) \end{aligned} u1sin(ωk⋅t)+v1cos(ωk⋅t)=u2sin(ωk⋅t)+v2cos(ωk⋅t)= cos(ωk⋅ϕ)sin(ωk⋅t)+sin(ωk⋅ϕ)cos(ωk⋅t)−sin(ωk⋅ϕ)sin(ωk⋅t)+cos(ωk⋅ϕ)cos(ωk⋅t)
相应的,可得:
u 1 = cos ( ω k . ϕ ) v 1 = sin ( ω k . ϕ ) u 2 = − sin ( ω k . ϕ ) v 2 = cos ( ω k . ϕ ) \begin{aligned} u_1 = \ \ \ \cos(\omega_k .\phi) & \ \ \ v_1 = \sin(\omega_k .\phi) \\ u_2 = - \sin(\omega_k . \phi) & \ \ \ v_2 = \cos(\omega_k .\phi) \end{aligned} u1= cos(ωk.ϕ)u2=−sin(ωk.ϕ) v1=sin(ωk.ϕ) v2=cos(ωk.ϕ)
所以,就得到了最终的矩阵 M M M为:
M ϕ , k = [ cos ( ω k ⋅ ϕ ) sin ( ω k ⋅ ϕ ) − sin ( ω k ⋅ ϕ ) cos ( ω k ⋅ ϕ ) ] M_{\phi,k} = \begin{bmatrix} \cos(\omega_k \cdot\phi) & \sin(\omega_k \cdot\phi) \\ - \sin(\omega_k \cdot \phi) & \cos(\omega_k \cdot\phi) \end{bmatrix} Mϕ,k=[cos(ωk⋅ϕ)−sin(ωk⋅ϕ)sin(ωk⋅ϕ)cos(ωk⋅ϕ)]
从上可以看出,最终的转换与 t t t无关。
类似地,我们可以找到其他正-余弦对的 M M M,最终允许我们表示 p t + ϕ ⃗ \vec{p_{t+\phi}} pt+ϕ为一个 p t ⃗ \vec{p_t} pt对任意固定偏移量 ϕ \phi ϕ的线性函数。这个属性,使模型很容易学得相对位置信息。
这解释了为什么要选择交替的正弦和余弦函数,仅通过正弦或余弦函数达不到这一点。
我们实现位置编码如下:
class PositionalEncoding(nn.Module):
def __init__(self, d_model, dropout, max_len=5000):
super(PositionalEncoding, self).__init__()
self.dropout = nn.Dropout(p=dropout)
# 位置编码矩阵,维度[max_len, embedding_dim]
pe = torch.zeros(max_len, d_model, device=DEVICE)
# 单词位置
position = torch.arange(0.0, max_len, device=DEVICE)
position.unsqueeze_(1)
# 使用exp和log实现幂运算
div_term = torch.exp(torch.arange(0.0, d_model, 2, device=DEVICE) * (- math.log(1e4) / d_model))
div_term.unsqueeze_(0)
# 计算单词位置沿词向量维度的纹理值
pe[:, 0 : : 2] = torch.sin(torch.mm(position, div_term))
pe[:, 1 : : 2] = torch.cos(torch.mm(position, div_term))
# 增加批次维度,[1, max_len, embedding_dim]
pe.unsqueeze_(0)
# 将位置编码矩阵注册为buffer(不参加训练),因为它是绝对位置编码
self.register_buffer('pe', pe)
def forward(self, x):
# 将一个批次中语句所有词向量与位置编码相加
# 注意,位置编码不参与训练,因此设置requires_grad=False
x += Variable(self.pe[:, : x.size(1), :], requires_grad=False)
return self.dropout(x)
编码器
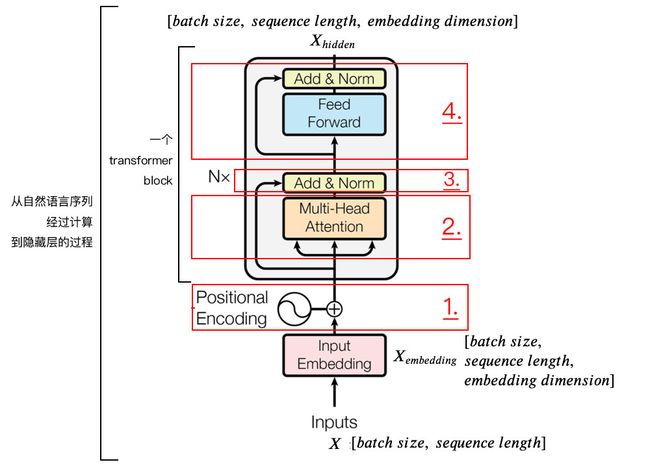
编码器由输入嵌入+位置编码+Transformer块(block)组成。
用于将自然语言序列转换为隐藏状态表征,可以完成一些主流NLP任务,如情感分类、语义关系分析和命名实体识别等。
其中输入 X X X是batch size个长度为sequence length的独热编码;经过输入嵌入层,增加了嵌入维度;然后经过Transformer块进行更加复杂的转换。
在Transformer块中主要有多头注意力、残差连接、层归一化与前馈神经网络。我们分别来看下。
自注意力
我们现在有了词向量句子和位置嵌入,假设我们有一些句子 X X X,其形状为[batch_size,sequence_length],首先我们在词向量里查到对应的嵌入,然后与位置嵌入元素相加,得到最终嵌入 X e m b e d d i n g X_{embedding} Xembedding形状为:[batch_size,sequence_length,embedding_dimension]。
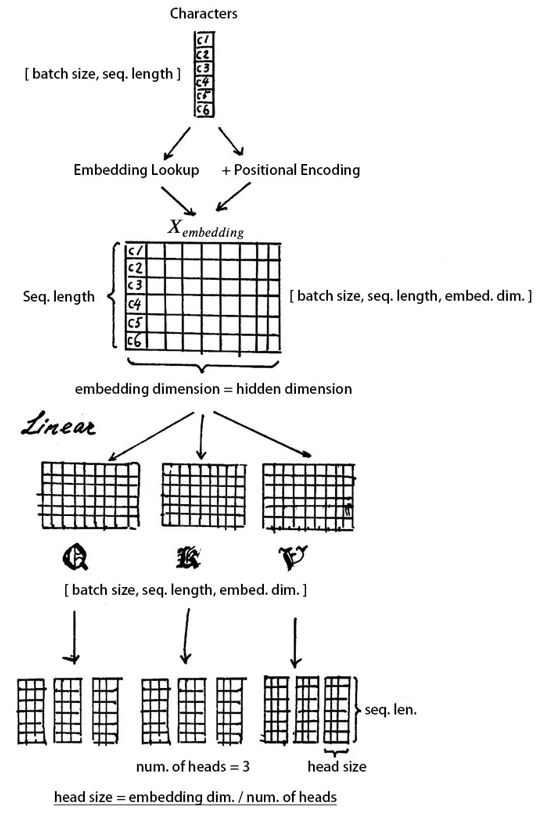
如上图所示, X e m b e d d i n g X_{embedding} Xembedding的计算公式为:
X e m b e d d i n g = E m b e d d i n g L o o k u p ( X ) + P o s i t i o i n a l E n c o d i n g ( X ) (2) X_{embedding} = EmbeddingLookup(X) + PositioinalEncoding(X) \tag 2 Xembedding=EmbeddingLookup(X)+PositioinalEncoding(X)(2)
接着,为了学到多重含义的表达,对 X e m b e d d i n g X_{embedding} Xembedding做线性映射,分别乘上三个权重 W Q , W K , W V ∈ R e m b e d _ d i m × e m b e d _ d i m W_Q,W_K,W_V \in \Bbb R^{embed\_dim \times embed\_dim} WQ,WK,WV∈Rembed_dim×embed_dim:
Q = L i n e a r ( X e m b e d d i n g ) = X e m b e d d i n g W Q K = L i n e a r ( X e m b e d d i n g ) = X e m b e d d i n g W K V = L i n e a r ( X e m b e d d i n g ) = X e m b e d d i n g W V (3) \begin{aligned} Q &= Linear(X_{embedding}) = X_{embedding}W_Q \\ K &= Linear(X_{embedding}) = X_{embedding}W_K \\ V &= Linear(X_{embedding}) = X_{embedding}W_V \\ \end{aligned} \tag 3 QKV=Linear(Xembedding)=XembeddingWQ=Linear(Xembedding)=XembeddingWK=Linear(Xembedding)=XembeddingWV(3)
然后准备进行多头注意力,为什么是多头的呢?
因为我们要用注意力机制来提取多重语义,我们首先定义一个超参数 h h h,即head的数量,这里嵌入维度(embedding dimension)必须能整除以 h h h,因为我们要把嵌入维度分割成 h h h份。
上图最后我们把嵌入维度分割成了 h h h份,分割后 Q , K , V Q,K,V Q,K,V的维度为[batch_size,sequence_length,h,embedding_dimension / h],之后我们把 Q , K , V Q,K,V Q,K,V中的sequence_length,h进行了一下转置,为了方便后续的计算。转置后的 Q , K , V Q,K,V Q,K,V的维度为[batch_size,h,sequence_length,embedding_dimension / h]。
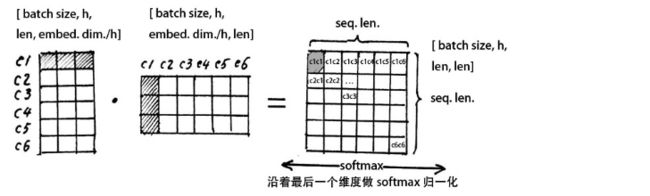
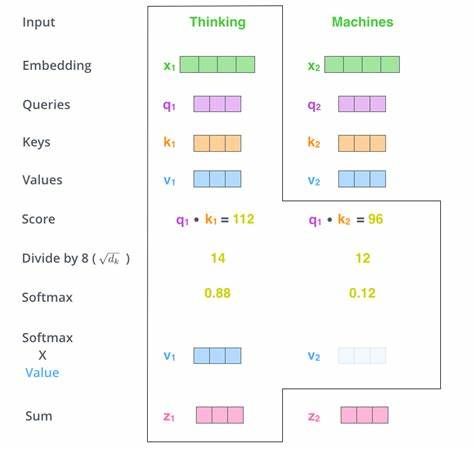
上图中,我们拿出一组heads来解释一下多头注意力的含义。我们拿出一组heads,即一组分割后的 Q , K , V Q,K,V Q,K,V,它们的维度都是[sequence_length,embedding_dimension / h],我们先计算 Q Q Q与 K K K的转置的点积,注意上图它们的维度。
两个向量越相似,它们的点积就越大。
我们在这里首先用代表第一个词的 c 1 c1 c1行与 c 1 c1 c1列相乘,得到一个数值,即位于注意力矩阵(上图最右边那个矩阵)的第 1 1 1行第 1 1 1列的 c 1 c 1 c1c1 c1c1,这里代表第一个词与自己的注意力得分,然后依次向后求得 c 1 c 2 , c 1 c 3 , ⋯ c1c2,c1c3,\cdots c1c2,c1c3,⋯。
注意力矩阵的第一行代表第一个词与这六个词的哪几个比较相关。
Attention ( Q , K , V ) = softmax ( Q K T d k ) V (4) \text{Attention}(Q,K,V) = \text{softmax} (\frac{QK^T}{\sqrt{d_k}})V \tag 4 Attention(Q,K,V)=softmax(dkQKT)V(4)
上式中就是自注意力机制,我们先求 Q K T QK^T QKT,也就是求出注意力矩阵,然后用注意力矩阵给 V V V加权, d k \sqrt{d_k} dk式为了把注意力矩阵变成标准正态分布,使得softmax归一化之后的结果更加稳定。
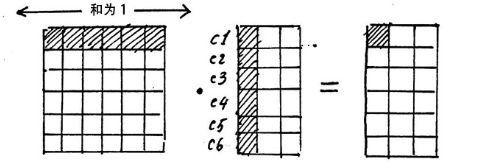
此时我们得到了注意力矩阵,并用softmax归一化,使得每个词与其他所有词的注意力权重之和为 1 1 1,注意力矩阵的作用就是一个注意力权重的概率分布,我们要用注意力矩阵的权重给 V V V进行加权,上图中我们从注意力矩阵取出一行(和为 1 1 1),然后依次点乘 V V V的列。
矩阵 V V V的每一行代表每个词向量的数学表达,我们上面的操作正是注意力权重进行这些数学表达的加权线性组合,从而使每个词向量都含有当前句子内所有词向量的信息。
注意进行点积运算之后, V V V的维度没有变化,还是[batch_size,h,sequence_length,embedding_dimension / h]。
d k \sqrt{d_{k}} dk归一化
假设 q \mathbf{q} q、 k \mathbf{k} k为均值0、方差1的独立随机变量,其点积注意力 q ⋅ k = ∑ i = 1 d k q i k i \mathbf{q} \cdot \mathbf{k} = \sum_{i=1}^{d_k}{\mathbf{q}_{i} \mathbf{k}_{i}} q⋅k=∑i=1dkqiki的均值和方差分别为0、 d k d_{k} dk。通过 d k \sqrt{d_{k}} dk缩放,使softmax结果更稳定(防止单词-单词间的点积注意力差异太大),便于反向传播时梯度平衡。
下面我们来实现多头注意,首先实现克隆帮助函数:
def clones(module, N):
"""
克隆基本单元,克隆的单元之间参数不共享
"""
return nn.ModuleList([
copy.deepcopy(module) for _ in range(N)
])
然后实现缩放注意力计算函数:
def attention(query, key, value, mask=None, dropout=None):
"""
Scaled Dot-Product Attention( 公式(4) )
"""
# q、k、v向量长度为d_k
d_k = query.size(-1)
# 矩阵乘法实现q、k点积注意力,sqrt(d_k)归一化
scores = torch.matmul(query, key.transpose(-2, -1)) / math.sqrt(d_k)
# 注意力掩码机制
if mask is not None:
scores = scores.masked_fill(mask==0, -1e9)
# 注意力矩阵softmax归一化
p_attn = F.softmax(scores, dim=-1)
# dropout
if dropout is not None:
p_attn = dropout(p_attn)
# 注意力对v加权
return torch.matmul(p_attn, value), p_attn
最后来实现多头注意力层:
class MultiHeadedAttention(nn.Module):
"""
Multi-Head Attention(前面图中编码器第2部分)
"""
def __init__(self, h, d_model, dropout=0.1):
super(MultiHeadedAttention, self).__init__()
"""
`h`:注意力头的数量
`d_model`:词向量维数
"""
# 确保整除
assert d_model % h == 0
# q、k、v向量维数
self.d_k = d_model // h
# 头的数量
self.h = h
# WQ、WK、WV矩阵及多头注意力拼接变换矩阵WO
self.linears = clones(nn.Linear(d_model, d_model), 4)
self.attn = None
self.dropout = nn.Dropout(p=dropout)
def forward(self, query, key, value, mask=None):
if mask is not None:
mask = mask.unsqueeze(1)
# 批次大小
nbatches = query.size(0)
# WQ、WK、WV分别对词向量线性变换,并将结果拆成h块
query, key, value = [
l(x).view(nbatches, -1, self.h, self.d_k).transpose(1, 2)
for l, x in zip(self.linears, (query, key, value))
]
# 注意力加权
x, self.attn = attention(query, key, value, mask=mask, dropout=self.dropout)
# 多头注意力加权拼接
x = x.transpose(1, 2).contiguous().view(nbatches, -1, self.h * self.d_k)
# 对多头注意力加权拼接结果线性变换
return self.linears[-1](x)
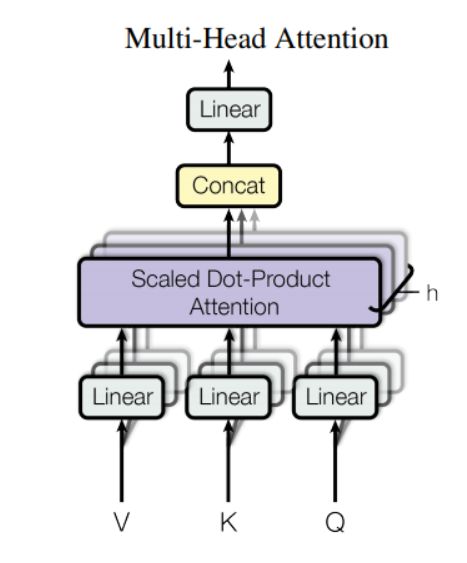
上面的代码实现了上图这样一个多头注意力,注意力这里实际上有4个线性变换,对应上面 self.linears = clones(nn.Linear(d_model, d_model), 4),分别是 Q , K , V Q,K,V Q,K,V和最上面拼接之后跟着的一个Linear层。
层归一化
层归一化针对每个输入的每个维度进行归一化操作。假设有 H H H个维度, x = ( x 1 , x 2 , ⋯ , x H ) x=(x_1,x_2,\cdots,x_H) x=(x1,x2,⋯,xH),层归一化首先计算这 H H H个维度的均值和方差,然后进行归一化得到 N ( x ) N(x) N(x),接着做一个缩放,类似批归一化。
μ = 1 H ∑ i = 1 H x i , σ = 1 H ∑ i = 1 H ( x i − μ ) 2 , N ( x ) = x − μ σ , h = α ⊙ N ( x ) + β (5) \mu = \frac{1}{H}\sum_{i=1}^H x_i,\quad \sigma = \sqrt{\frac{1}{H}\sum_{i=1}^H (x_i - \mu)^2}, \quad N(x) = \frac{x-\mu}{\sigma},\quad h = \alpha \,\odot N(x) + \beta \tag{5} μ=H1i=1∑Hxi,σ=H1i=1∑H(xi−μ)2,N(x)=σx−μ,h=α⊙N(x)+β(5)
其中, ⊙ \odot ⊙表示Hadamard积,即两个向量对应元素相乘; h h h就是LN层的输出; μ \mu μ和 σ \sigma σ是输入各个维度的均值和方差; α \alpha α和 β \beta β是两个可学习的参数;和 h h h的维度相同。
class LayerNorm(nn.Module):
def __init__(self, features, eps=1e-6):
super(LayerNorm, self).__init__()
# α、β分别初始化为1、0
self.a_2 = nn.Parameter(torch.ones(features))
self.b_2 = nn.Parameter(torch.zeros(features))
# 平滑项
self.eps = eps
def forward(self, x):
# 沿词向量方向计算均值和方差
mean = x.mean(dim=-1, keepdim=True)
std = x.std(dim=-1, keepdim=True)
# 沿词向量和语句序列方向计算均值和方差
# mean = x.mean(dim=[-2, -1], keepdim=True)
# std = x.std(dim=[-2, -1], keepdim=True)
# 归一化
x = (x - mean) / torch.sqrt(std ** 2 + self.eps)
return self.a_2 * x + self.b_2
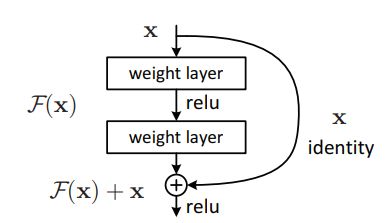
残差连接
假设网络中某层输入 x x x后的输出为 F ( x ) F(x) F(x),不管激活函数是什么,经过深层网络都可能导致梯度消失的情况。增加残差连接,相当于某层输入 x x x后的输出为 F ( x ) + x F(x) + x F(x)+x。最坏的情况相当于没有经过 F ( x ) F(x) F(x)这一层,直接输入到高层,这样高层的表现至少能和低层一样好。
这里 SubLayer \text{SubLayer} SubLayer就是上面说的 F F F。训练时,梯度通过捷径直接反向传播至前层
x + SubLayer ( x ) (6) \mathbf{x} + \text{SubLayer}(\mathbf{x}) \tag{6} x+SubLayer(x)(6)
其中, SubLayer \text{SubLayer} SubLayer表示Add & Norm前层模块,如Multi-Head Attention、Feed Forward。
class SublayerConnection(nn.Module):
"""
封装了层归一化和残差链接,中间的sublayer是多头注意力或前馈网络
"""
def __init__(self, size, dropout):
super(SublayerConnection, self).__init__()
self.norm = LayerNorm(size)
self.dropout = nn.Dropout(dropout)
def forward(self, x, sublayer):
# 层归一化
x_ = self.norm(x)
# 真正的子层(多头注意力或前馈网络)
x_ = sublayer(x_)
# 还要经过Dropout
x_ = self.dropout(x_)
# 残差连接
return x + x_
前馈网络
前馈网络(Feed Forward)为两层线性映射及激活函数。
class PositionwiseFeedForward(nn.Module):
def __init__(self, d_model, d_ff, dropout=0.1):
super(PositionwiseFeedForward, self).__init__()
self.w_1 = nn.Linear(d_model, d_ff) # 线性变换
self.w_2 = nn.Linear(d_ff, d_model) # 线性变换
self.dropout = nn.Dropout(dropout)
def forward(self, x):
x = self.w_1(x)
x = F.relu(x)
x = self.dropout(x)
x = self.w_2(x)
return x
编码器整体架构
Transformer编码器基本单元由两个子层组成:第一个子层实现多头 自注意力(self-attention机制(Multi-Head Attention);第二个子层实现全连接前馈网络。计算过程如下:
- 词向量与位置编码
X = EmbeddingLookup ( X ) + PositionalEncoding (7) X = \text{EmbeddingLookup}(X) + \text{PositionalEncoding} \tag{7} X=EmbeddingLookup(X)+PositionalEncoding(7)
得到
X ∈ R batch_size × seq_len × embedding_dim X \in \mathbb{R}^{\text{batch\_size} \times \text{seq\_len} \times \text{embedding\_dim}} X∈Rbatch_size×seq_len×embedding_dim
- 自注意力机制
Q = Linear ( X ) = X W Q Q = \text{Linear}(X) = X W_{Q} Q=Linear(X)=XWQ
K = Linear ( X ) = X W K (8) K = \text{Linear}(X) = XW_{K} \tag{8} K=Linear(X)=XWK(8)
V = Linear ( X ) = X W V V = \text{Linear}(X) = XW_{V} V=Linear(X)=XWV
X attention = SelfAttention ( Q , K , V ) (9) X_{\text{attention}} = \text{SelfAttention}(Q, K, V) \tag{9} Xattention=SelfAttention(Q,K,V)(9)
- 层归一化、残差连接
X attention = LayerNorm ( X attention ) (10) X_{\text{attention}} = \text{LayerNorm}(X_{\text{attention}}) \tag{10} Xattention=LayerNorm(Xattention)(10)
X attention = X + X attention (11) X_{\text{attention}} = X + X_{\text{attention}} \tag{11} Xattention=X+Xattention(11)
- 前馈网络
X hidden = Linear ( Activate ( Linear ( X attention ) ) ) (12) X_{\text{hidden}} = \text{Linear}(\text{Activate}(\text{Linear}(X_{\text{attention}}))) \tag{12} Xhidden=Linear(Activate(Linear(Xattention)))(12)
- 层归一化、残差连接
X hidden = LayerNorm ( X hidden ) (13) X_{\text{hidden}} = \text{LayerNorm}(X_{\text{hidden}}) \tag{13} Xhidden=LayerNorm(Xhidden)(13)
X hidden = X attention + X hidden (14) X_{\text{hidden}} = X_{\text{attention}} + X_{\text{hidden}} \tag{14} Xhidden=Xattention+Xhidden(14)
其中
X hidden ∈ R batch_size × seq_len × embedding_dim X_{\text{hidden}} \in \mathbb{R}^{\text{batch\_size} \times \text{seq\_len} \times \text{embedding\_dim}} Xhidden∈Rbatch_size×seq_len×embedding_dim
Transformer编码器由 N = 6 N = 6 N=6个编码器基本单元组成。
然后基于上面的构建,我们来实现编码器层:
class EncoderLayer(nn.Module):
def __init__(self, size, self_attn, feed_forward, dropout):
super(EncoderLayer, self).__init__()
self.self_attn = self_attn # 多头注意力
self.feed_forward = feed_forward # 前馈网络
# SublayerConnection作用连接multi和ffn
self.sublayer = clones(SublayerConnection(size, dropout), 2)
# d_model
self.size = size
def forward(self, x, mask):
# 将embedding层进行多头注意力
x = self.sublayer[0](x, lambda x: self.self_attn(x, x, x, mask)) # 先是多头注意力
# attn的结果直接作为下一层输入
return self.sublayer[1](x, self.feed_forward) # 然后是前馈网络
而编码器就是 N N N个编码器层的叠加:
class Encoder(nn.Module):
def __init__(self, layer, N):
"""
layer = EncoderLayer
"""
super(Encoder, self).__init__()
# 复制N个编码器基本单元
self.layers = clones(layer, N)
# 层归一化
self.norm = LayerNorm(layer.size)
def forward(self, x, mask):
"""
循环编码器基本单元N次
"""
for layer in self.layers:
x = layer(x, mask) # 叠加N次
return self.norm(x) # 最后经过层归一化
编码器了解完了,下面我们来看解码器。
解码器
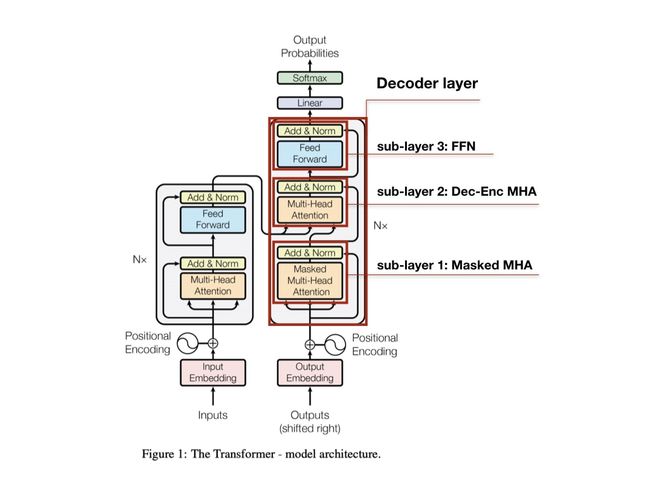
解码器同样由 N N N层解码器基本单元堆叠而成,与编码器基本单元不同的是:解码器在编码器基本单元的多头自注意力机制及前馈网络之间插入一个上下文注意力(context-attention机制(Multi-Head Attention)层,用解码器基本单元的自注意力机制输出作为 q q q查询编码器的输出,以便解码时,解码器获得编码器的所有输出,即上下文注意力机制的 K K K和 V V V来自编码器的输出, Q Q Q来自解码器前一时刻的输出。
从上图可以看到,解码器有3个子层(SubLayer)。
解码器基本单元的输入、输出:
-
输入:编码器的输出、解码器前一时刻的输出
-
输出:对应当前时刻输出单词的概率分布
此外,解码器的输出(最后一个解码器基本单元的输出)需要经线性变换和softmax函数映射为下一时刻预测单词的概率分布。
解码器解码过程:给定编码器输出(编码器输入语句所有单词的词向量)和解码器前一时刻输出(单词),预测当前时刻单词的概率分布。
注意:训练过程中,编、解码器均可以并行计算(训练语料中已知前一时刻单词);推理过程中,编码器可以并行计算,解码器需要像RNN一样依次预测输出单词。
下面我们看一下解码器层的实现:
class DecoderLayer(nn.Module):
def __init__(self, size, self_attn, src_attn, feed_forward, dropout):
super(DecoderLayer, self).__init__()
self.size = size
# 自注意力机制
self.self_attn = self_attn
# 上下文注意力机制
self.src_attn = src_attn
# 前馈网络
self.feed_forward = feed_forward
self.sublayer = clones(SublayerConnection(size, dropout), 3) # 解码器有三个子层
def forward(self, x, memory, src_mask, tgt_mask):
# memory为编码器输出隐藏表示
m = memory
# 自注意力机制,q、k、v均来自解码器隐表示 (子层一)
x = self.sublayer[0](x, lambda x: self.self_attn(x, x, x, tgt_mask))
# 上下文注意力机制:q为来自解码器隐表示,而k、v为编码器隐表示 (子层二)
x = self.sublayer[1](x, lambda x: self.src_attn(x, m, m, src_mask))
# 接下来是前馈网络(子层三)
return self.sublayer[2](x, self.feed_forward)
解码器的实现,主要是克隆了 N N N个解码器层,最后的输出经过层归一化:
class Decoder(nn.Module):
def __init__(self, layer, N):
super(Decoder, self).__init__()
self.layers = clones(layer, N)
self.norm = LayerNorm(layer.size)
def forward(self, x, memory, src_mask, tgt_mask):
"""
循环解码器基本单元N次
"""
for layer in self.layers:
x = layer(x, memory, src_mask, tgt_mask)
return self.norm(x)
解码器最上面的部分作为生成器(generator),由线性层+Softmax层组成:
class Generator(nn.Module):
"""
解码器输出经线性变换和softmax函数映射为下一时刻预测单词的概率分布
"""
def __init__(self, d_model, vocab):
super(Generator, self).__init__()
# decode后的结果,先进入一个全连接层变为词典大小的向量
self.proj = nn.Linear(d_model, vocab)
def forward(self, x):
# 然后再进行log_softmax操作(在softmax结果上再做多一次log运算)
return F.log_softmax(self.proj(x), dim=-1)
基本上介绍的差不多了,除了还有一个细节——注意力掩码。
注意力掩码
注意力掩码在编码器和解码器中作用不同。
编码器注意力掩码
我们知道,自然语言处理中,文本语句批次数据内通常长度不一,因此需要为短语句进行填充,而填充的字符是不需要参与注意力计算的。
因此,编码器注意力掩码的目地:使批次中较短语句的填充部分不参与注意力计算。
模型训练通常按批次进行,同一批次中的语句长度可能不同,因此需要按语句最大长度对短语句进行0填充以补齐长度。语句填充部分属于无效信息,不应参与前向传播,考虑softmax函数特性,
softmax ( z ) i = exp ( z i ) ∑ j = 1 K exp ( z j ) (15) \text{softmax}(\mathbf {z})_{i} = {\frac{\exp(z_{i})}{\sum _{j = 1}^{K} \exp(z_{j})}} \tag{15} softmax(z)i=∑j=1Kexp(zj)exp(zi)(15)
当 z i z_{i} zi为填充时,可令 z i = − ∞ z_{i} = - \infty zi=−∞(一般取很大的负数)使其无效,即
z pad = − ∞ ⇒ exp ( z pad ) = 0 z_{\text{pad}} = - \infty \quad \Rightarrow \quad \exp(z_{\text{pad}}) = 0 zpad=−∞⇒exp(zpad)=0
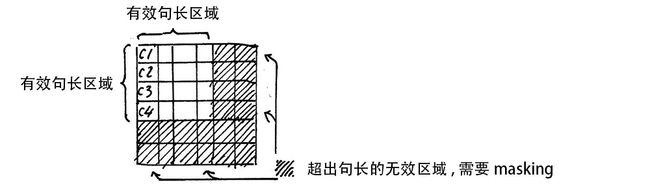
这里我们只要设定一个足够大的负数即可,编码器注意力掩码生成伪代码:
# True表示有效;False表示无效(填充位)
mask = src != pad # 这里是矩阵运算,mask中为true的即为非填充字符,为false的为填充字符
# 将无效位置为负无穷
scores = scores.masked_fill(~mask, -1e9) # ~mask,取反,将为false的填充字符设成-1e9
接下来我们看下解码器注意力掩码。
解码器注意力掩码
解码器注意力掩码相对于编码器略微复杂,不仅需要将填充部分屏蔽掉,还需要对当前及后续序列进行屏蔽(subsequent_mask),防止作弊。
即解码器在预测当前时刻单词时,不能知道当前及后续单词内容,因此注意力掩码需要将当前时刻之后的注意力分数全部置为 − ∞ - \infty −∞,然后再计算 s o f t m a x softmax softmax,防止发生数据泄露。
subsequent_mask的矩阵形式为一个下三角矩阵,在主对角线右上位置全部为False。

我们来看下这种屏蔽是如何做到的。
def subsequent_mask(size):
'''
为后续输出序列的位置添加屏蔽
:param size: 输出序列长度
'''
attn_shape = (1, size, size)
# 主对角线上移一位,主对角线下的元素全为0
mask = np.triu(np.ones(attn_shape), k=1).astype('uint8')
return torch.from_numpy(mask) == 0
np.triu是干嘛的?
np.triu(a, k)是取矩阵a的上三角数据,这个三角数据的斜线位置由k决定,并且斜线下方都为0。
import numpy as np
a = np.arange(1,17).reshape(4,-1)
print(a)
[[ 1 2 3 4]
[ 5 6 7 8]
[ 9 10 11 12]
[13 14 15 16]]
当np.triu(a, k = 0)时,得到包含主对角线的上三角数据。
print(np.triu(a, k = 0))
[[ 1 2 3 4]
[ 0 6 7 8]
[ 0 0 11 12]
[ 0 0 0 16]]
当np.triu(a, k = 1)时,主对角线上移一位。
print(np.triu(a, k = 1))
[[ 0 2 3 4]
[ 0 0 7 8]
[ 0 0 0 12]
[ 0 0 0 0]]
当np.triu(a, k = -1)时,主对角线下移一位。
print(np.triu(a, k = -1))
[[ 1 2 3 4]
[ 5 6 7 8]
[ 0 10 11 12]
[ 0 0 15 16]]
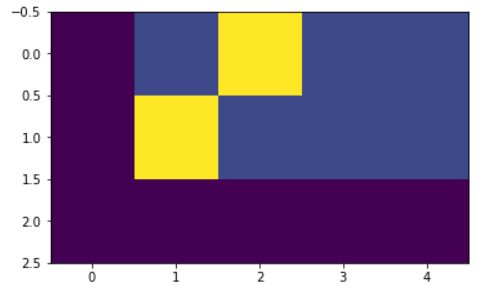
注意力mask下面显示了每个tgt(目标)单词(行)允许查看的位置(列)。在训练过程中,当前单词后面的单词会被屏蔽。
plt.figure(figsize=(5,5))
plt.imshow(subsequent_mask(20)[0])
比如第0行,只能看到1列,第1行只能看到2列。黄色的区域代表可以看到的列。
本小节最后,我们就可以实现批次类,
class Batch:
"""
批次类
1. 输入序列(源)
2. 输出序列(目标)
3. 构造掩码
"""
def __init__(self, src, trg=None, pad=PAD):
'''
:param src: 源数据 [batch_size, input_len]
:param trg: 目标数据 [batch_size, input_len]
'''
# 将输入、输出单词id表示的数据规范成整数类型
src = torch.from_numpy(src).to(DEVICE).long()
trg = torch.from_numpy(trg).to(DEVICE).long()
self.src = src
# 对于当前输入的语句非空部分进行判断,bool序列
# 并在seq length前面增加一维,形成维度为 1×seq length 的矩阵
self.src_mask = (src != pad).unsqueeze(-2)
# 如果输出目标不为空,则需要对解码器使用的目标语句进行掩码
if trg is not None:
# 解码器使用的目标输入部分
self.trg = trg[:, :-1] # 去掉最后一个,可用于teacher forcing,此时self.trg维度变成了[batch_size, input_len-1]
# 去掉第一个,构建目标输出
self.trg_y = trg[:, 1:]
# 目标mask的目的是防止当前位置注意到后面的位置 [batch_size,input_len-1, input_len-1]
self.trg_mask = self.make_std_mask(self.trg, pad)
# 实际单词(不包括填充词)数量
self.ntokens = (self.trg_y != pad).data.sum()
# 掩码操作
@staticmethod
def make_std_mask(tgt, pad):
tgt_mask = (tgt != pad).unsqueeze(-2) # 在倒数第二个位置加入一个维度
# type_as 把调用tensor的类型变成给定tensor的
tgt_mask = tgt_mask & Variable(subsequent_mask(tgt.size(-1)).type_as(tgt_mask.data))
return tgt_mask
Transformer模型
大部分有竞争力的神经网络序列转导模型都有一个编码器-解码器(Encoder-Decoder)结构。编码器映射一个用符号表示的输入序列 ( x 1 , ⋯ , x n ) (x_1,\cdots,x_n) (x1,⋯,xn)到一个连续的序列表示 z = ( z 1 , ⋯ , z n ) z=(z_1,\cdots, z_n) z=(z1,⋯,zn)。给定 z z z,解码器生成符号的一个输出序列 ( y 1 , ⋯ , y m ) (y_1,\cdots,y_m) (y1,⋯,ym),一次生成一个元素。在每个时间步,模型是自回归(auto-regressive)的,在生成下个输出时消耗上一次生成的符号作为附加的输入。
实际上Transformer就是一编码器-解码器架构。
class Transformer(nn.Module):
def __init__(self, encoder, decoder, src_embed, tgt_embed, generator):
super(Transformer, self).__init__()
self.encoder = encoder
self.decoder = decoder
self.src_embed = src_embed
self.tgt_embed = tgt_embed
self.generator = generator
def encode(self, src, src_mask):
return self.encoder(self.src_embed(src), src_mask)
def decode(self, memory, src_mask, tgt, tgt_mask):
return self.decoder(self.tgt_embed(tgt), memory, src_mask, tgt_mask)
def forward(self, src, tgt, src_mask, tgt_mask):
# encoder的结果作为decoder的memory参数传入,进行decode
return self.decode(self.encode(src, src_mask), src_mask, tgt, tgt_mask)
然后我们实现构建Transformer模型的函数:
def make_model(src_vocab, tgt_vocab, N=6, d_model=512, d_ff=2048, h = 8, dropout=0.1):
c = copy.deepcopy
# 实例化Attention对象
attn = MultiHeadedAttention(h, d_model).to(DEVICE)
# 实例化FeedForward对象
ff = PositionwiseFeedForward(d_model, d_ff, dropout).to(DEVICE)
# 实例化PositionalEncoding对象
position = PositionalEncoding(d_model, dropout).to(DEVICE)
# 实例化Transformer模型对象
model = Transformer(
Encoder(EncoderLayer(d_model, c(attn), c(ff), dropout).to(DEVICE), N).to(DEVICE),
Decoder(DecoderLayer(d_model, c(attn), c(attn), c(ff), dropout).to(DEVICE), N).to(DEVICE),
nn.Sequential(Embeddings(d_model, src_vocab).to(DEVICE), c(position)),
nn.Sequential(Embeddings(d_model, tgt_vocab).to(DEVICE), c(position)),
Generator(d_model, tgt_vocab)).to(DEVICE)
# This was important from their code.
# Initialize parameters with Glorot / fan_avg.
for p in model.parameters():
if p.dim() > 1:
# 这里初始化采用的是nn.init.xavier_uniform
nn.init.xavier_uniform_(p)
return model.to(DEVICE)
模型训练
标签平滑
训练过程中,采用KL散度损失实现标签平滑( ϵ l s = 0.1 \epsilon_{ls} = 0.1 ϵls=0.1)策略,提高模型鲁棒性、准确性和BLEU分数。
标签平滑:输出概率分布由one-hot方式转为真实标签的概率置为confidence,其它所有非真实标签概率平分1 - confidence。
class LabelSmoothing(nn.Module):
"""
标签平滑
"""
def __init__(self, size, padding_idx, smoothing=0.0):
super(LabelSmoothing, self).__init__()
self.criterion = nn.KLDivLoss(reduction='sum')
self.padding_idx = padding_idx
self.confidence = 1.0 - smoothing
self.smoothing = smoothing
self.size = size
self.true_dist = None
def forward(self, x, target):
assert x.size(1) == self.size
true_dist = x.data.clone()
true_dist.fill_(self.smoothing / (self.size - 2))
true_dist.scatter_(1, target.data.unsqueeze(1), self.confidence)
true_dist[:, self.padding_idx] = 0
mask = torch.nonzero(target.data == self.padding_idx)
if mask.dim() > 0:
true_dist.index_fill_(0, mask.squeeze(), 0.0)
self.true_dist = true_dist
return self.criterion(x, Variable(true_dist, requires_grad=False))
标签平滑的例子:
# Label smoothing的例子
crit = LabelSmoothing(5, 0, 0.4) # 设定一个ϵ=0.4
predict = torch.FloatTensor([[0, 0.2, 0.7, 0.1, 0],
[0, 0.2, 0.7, 0.1, 0],
[0, 0.2, 0.7, 0.1, 0]])
v = crit(Variable(predict.log()),
Variable(torch.LongTensor([2, 1, 0])))
# Show the target distributions expected by the system.
print(crit.true_dist)
plt.imshow(crit.true_dist)
tensor([[0.0000, 0.1333, 0.6000, 0.1333, 0.1333],
[0.0000, 0.6000, 0.1333, 0.1333, 0.1333],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000]])
计算损失
class SimpleLossCompute:
"""
简单的计算损失和进行参数反向传播更新训练的函数
"""
def __init__(self, generator, criterion, opt=None):
self.generator = generator
self.criterion = criterion
self.opt = opt
def __call__(self, x, y, norm):
x = self.generator(x)
loss = self.criterion(x.contiguous().view(-1, x.size(-1)),
y.contiguous().view(-1)) / norm
loss.backward()
if self.opt is not None:
self.opt.step()
self.opt.optimizer.zero_grad()
return loss.data.item() * norm.float()
优化器
Adam优化器, β 1 = 0.9 、 β 2 = 0.98 \beta_1=0.9、\beta_2=0.98 β1=0.9、β2=0.98 和 ϵ = 1 0 − 9 \epsilon = 10^{−9} ϵ=10−9,并使用warmup策略调整学习率:
l r = d model − 0.5 min ( step_num − 0.5 , step_num × warmup_steps − 1.5 ) lr = d_{\text{model}}^{−0.5} \min(\text{step\_num}^{−0.5}, \text{step\_num} \times \text{warmup\_steps}^{−1.5}) lr=dmodel−0.5min(step_num−0.5,step_num×warmup_steps−1.5)
使用固定步数 warmup_steps \text{warmup\_steps} warmup_steps先使学习率的线性增长(热身),而后随着 step_num \text{step\_num} step_num的增加以 step_num \text{step\_num} step_num的反平方根成比例逐渐减小学习率。
class NoamOpt:
"Optim wrapper that implements rate."
def __init__(self, model_size, factor, warmup, optimizer):
self.optimizer = optimizer
self._step = 0
self.warmup = warmup
self.factor = factor
self.model_size = model_size
self._rate = 0
def step(self):
"Update parameters and rate"
self._step += 1
rate = self.rate()
for p in self.optimizer.param_groups:
p['lr'] = rate
self._rate = rate
self.optimizer.step()
def rate(self, step = None):
"Implement `lrate` above"
if step is None:
step = self._step
return self.factor * (self.model_size ** (-0.5) * min(step ** (-0.5), step * self.warmup ** (-1.5)))
def get_std_opt(model):
return NoamOpt(model.src_embed[0].d_model, 2, 4000,
torch.optim.Adam(model.parameters(), lr=0, betas=(0.9, 0.98), eps=1e-9))
主要调节是在 r a t e rate rate 这个函数中,其中
- m o d e l _ s i z e model\_size model_size 即为 d m o d e l d_{model} dmodel
- w a r m u p warmup warmup 即为 w a r m u p _ s t e p s warmup\_steps warmup_steps
- f a c t o r factor factor 可以理解为初始的学习率
以下对该优化器在不同模型大小( m o d e l _ s i z e model\_size model_size)和不同超参数( m a r m u p marmup marmup)值的情况下的学习率( l r a t e lrate lrate)曲线进行示例。
# Three settings of the lrate hyperparameters.
opts = [NoamOpt(512, 1, 4000, None),
NoamOpt(512, 1, 8000, None),
NoamOpt(256, 1, 4000, None)]
plt.plot(np.arange(1, 20000), [[opt.rate(i) for opt in opts] for i in range(1, 20000)])
plt.legend(["512:4000", "512:8000", "256:4000"])
训练
接下来,我们创建一个通用的训练和评分功能来跟踪损失。 我们传入一个上面定义的损失计算函数,它也处理参数更新。
def run_epoch(data, model, loss_compute, epoch):
start = time.time()
total_tokens = 0.
total_loss = 0.
tokens = 0.
for i , batch in enumerate(data):
out = model(batch.src, batch.trg, batch.src_mask, batch.trg_mask)
loss = loss_compute(out, batch.trg_y, batch.ntokens)
total_loss += loss
total_tokens += batch.ntokens
tokens += batch.ntokens
if i % 50 == 1:
elapsed = time.time() - start
print("Epoch %d Batch: %d Loss: %f Tokens per Sec: %fs" % (epoch, i - 1, loss / batch.ntokens, (tokens.float() / elapsed / 1000.)))
start = time.time()
tokens = 0
return total_loss / total_tokens
def train(data, model, criterion, optimizer):
"""
训练并保存模型
"""
# 初始化模型在dev集上的最优Loss为一个较大值
best_dev_loss = 1e5
for epoch in range(EPOCHS):
# 模型训练
model.train()
run_epoch(data.train_data, model, SimpleLossCompute(model.generator, criterion, optimizer), epoch)
model.eval()
# 在dev集上进行loss评估
print('>>>>> Evaluate')
dev_loss = run_epoch(data.dev_data, model, SimpleLossCompute(model.generator, criterion, None), epoch)
print('<<<<< Evaluate loss: %f' % dev_loss)
# 如果当前epoch的模型在dev集上的loss优于之前记录的最优loss则保存当前模型,并更新最优loss值
if dev_loss < best_dev_loss:
torch.save(model.state_dict(), SAVE_FILE)
best_dev_loss = dev_loss
print('****** Save model done... ******')
print()
然后就可以进行训练了
# 数据预处理
data = PrepareData(TRAIN_FILE, DEV_FILE)
src_vocab = len(data.en_word_dict)
tgt_vocab = len(data.cn_word_dict)
print("src_vocab %d" % src_vocab)
print("tgt_vocab %d" % tgt_vocab)
# 初始化模型
model = make_model(
src_vocab,
tgt_vocab,
LAYERS,
D_MODEL,
D_FF,
H_NUM,
DROPOUT
)
# 训练
print(">>>>>>> start train")
train_start = time.time()
criterion = LabelSmoothing(tgt_vocab, padding_idx = 0, smoothing= 0.0)
optimizer = NoamOpt(D_MODEL, 1, 2000, torch.optim.Adam(model.parameters(), lr=0, betas=(0.9,0.98), eps=1e-9))
train(data, model, criterion, optimizer)
print(f"<<<<<<< finished train, cost {time.time()-train_start:.4f} seconds")
模型预测
训练好了之后,我们用模型进行预测来看一下效果:
def greedy_decode(model, src, src_mask, max_len, start_symbol):
"""
传入一个训练好的模型,对指定数据进行预测
"""
# 先用encoder进行encode
memory = model.encode(src, src_mask)
# 初始化预测内容为1×1的tensor,填入开始符('BOS')的id,并将type设置为输入数据类型(LongTensor)
ys = torch.ones(1, 1).fill_(start_symbol).type_as(src.data)
# 遍历输出的长度下标
for i in range(max_len-1):
# decode得到隐层表示
out = model.decode(memory,
src_mask,
Variable(ys),
Variable(subsequent_mask(ys.size(1)).type_as(src.data)))
# 将隐藏表示转为对词典各词的log_softmax概率分布表示
prob = model.generator(out[:, -1])
# 获取当前位置最大概率的预测词id
_, next_word = torch.max(prob, dim = 1)
next_word = next_word.data[0]
# 将当前位置预测的字符id与之前的预测内容拼接起来
ys = torch.cat([ys,
torch.ones(1, 1).type_as(src.data).fill_(next_word)], dim=1)
return ys
def evaluate(data, model):
"""
在data上用训练好的模型进行预测,打印模型翻译结果
"""
# 梯度清零
with torch.no_grad():
# 在data的英文数据长度上遍历下标
for i in range(len(data.dev_en)):
# 打印待翻译的英文语句
en_sent = " ".join([data.en_index_dict[w] for w in data.dev_en[i]])
print("\n" + en_sent)
# 打印对应的中文语句答案
cn_sent = " ".join([data.cn_index_dict[w] for w in data.dev_cn[i]])
print("".join(cn_sent))
# 将当前以单词id表示的英文语句数据转为tensor,并放如DEVICE中
src = torch.from_numpy(np.array(data.dev_en[i])).long().to(DEVICE)
# 增加一维
src = src.unsqueeze(0)
# 设置attention mask
src_mask = (src != 0).unsqueeze(-2)
# 用训练好的模型进行decode预测
out = greedy_decode(model, src, src_mask, max_len=MAX_LENGTH, start_symbol=data.cn_word_dict["BOS"])
# 初始化一个用于存放模型翻译结果语句单词的列表
translation = []
# 遍历翻译输出字符的下标(注意:开始符"BOS"的索引0不遍历)
for j in range(1, out.size(1)):
# 获取当前下标的输出字符
sym = data.cn_index_dict[out[0, j].item()]
# 如果输出字符不为'EOS'终止符,则添加到当前语句的翻译结果列表
if sym != 'EOS':
translation.append(sym)
# 否则终止遍历
else:
break
# 打印模型翻译输出的中文语句结果
print("translation: %s" % " ".join(translation))
# 预测
# 加载模型
model.load_state_dict(torch.load(SAVE_FILE))
# 开始预测
print(">>>>>>> start evaluate")
evaluate_start = time.time()
evaluate(data, model)
print(f"<<<<<<< finished evaluate, cost {time.time()-evaluate_start:.4f} seconds")
BOS look around . EOS
BOS 四 处 看 看 。 EOS
translation: 看 !
BOS hurry up . EOS
BOS 赶 快 ! EOS
translation: 快 点 !
BOS keep trying . EOS
BOS 继 续 努 力 。 EOS
translation: 继 续 努 力 。
BOS take it . EOS
BOS 拿 走 吧 。 EOS
translation: 去 拿 吧 。
BOS birds fly . EOS
BOS 鸟 类 飞 行 。 EOS
translation: 鸟 类 飞 行 。
BOS hurry up . EOS
BOS 快 点 ! EOS
translation: 快 点 !
BOS look there . EOS
BOS 看 那 里 。 EOS
translation: 看 那 里 看 见 。
BOS how annoying ! EOS
BOS 真 烦 人 。 EOS
translation: 真 烦 人 。
BOS get serious . EOS
BOS 认 真 点 。 EOS
translation: 认 真 点 。
BOS once again . EOS
BOS 再 一 次 。 EOS
translation: 再 次 一 次 。
BOS stay sharp . EOS
BOS 保 持 警 惕 。 EOS
translation: 保 持 警 惕 。
BOS i won ! EOS
BOS 我 赢 了 。 EOS
translation: 我 赢 得 了 。
BOS get away ! EOS
BOS 滚 ! EOS
translation: 走 开 !
BOS i resign . EOS
BOS 我 放 弃 。 EOS
translation: 我 放 弃 。
BOS how strange ! EOS
BOS 真 奇 怪 。 EOS
translation: 真 奇 怪 。
...
参考
- 深入浅出Transformer
- 贪心学院课程